content (node parent)
カテゴリごとのコマンド
AGV
agvaddlistener (obj agv, node listenernode, num flags[, ...])
説明
AGVにイベントリスナーを追加する
例
agvaddlistener(agv, c, AGV_LISTEN_PRE_ARRIVAL);
agvinfo (obj agv, num what[, p1, p2, p3, p4])
説明
廃止されました。AGVクラスを使用してください。
パラメータに応じて、AGVについての各種の情報を取得します。
AGV_CURRENT_CP - AGVの現在のコントロールポイントを返します。
AGV_ORIGIN_CP - AGVの元のコントロールポイントを返します。
AGV_INTERMEDIATE_DEST_CP - AGVの中間目的地コントロールポイントを返します。
AGV_DEST_CP - AGV_INTERMEDIATE_DEST_CPと同じです。
AGV_FINAL_DEST_CP - AGVの最終目的地のコントロールポイントを返します。
AGV_DEST - AGVの目的地オブジェクトを返します。
AGV_BATTERY_LEVEL - AGVの現在のバッテリーレベルをバッテリー容量のパーセンテージ(0~100)で返します。
AGV_AMP_HOURS - AGVの現在のバッテリーレベルをアンペア時で返します。
AGV_START_RECHARGE - AGVの再充電を開始します。最大容量まで再充電するため必要な時間を返します。
AGV_RECHARGE_TO_LEVEL - AGVのバッテリーレベルをp1(0~100)に明示的に設定します。
AGV_ADD_ALLOC_POINT - 移動初期化トリガーから呼び出します。割り当てのコントロールポイント/コントロールエリアを手動で割り当てます。これらは、AGVの現在の移動パスの一部として割り当てる必要がないコントロールポイント/コントロールエリアです。コントロールポイント/コントロールエリアはp1として渡され、どの距離で割り当てる必要があるかがp2として渡されます。このコマンドは、その割り当てを表すノードへの参照を返します。その割り当てポイントについてさらにデータを指定するには、AGV_SET_ALLOC_POINT_DEALLOC_DISTとAGV_SET_CAN_STOP_AT_ALLOC_POINTを使用します。
AGV_SET_ALLOC_POINT_DEALLOC_DIST - 追加された手動の割り当てポイントについて、AGVがオブジェクトを割り当て解除できる移動距離を設定します。オブジェクトが正しく割り当て解除されるよう、割り当ての追加後にいずれかの時点でこのコマンドを呼び出します。p1はAGV_ADD_ALLOC_POINTにより返される割り当てポイントノードへの参照、p2は割り当て解除距離です。
AGV_SET_CAN_STOP_AT_ALLOC_POINT - AGVが、手動で追加された割り当てポイントで停止可能かどうかを設定します。デフォルトはnoで、AGVは停止距離では停止せず、オブジェクトの割り当てを試みる前に次の停止可能なポイントまで続行します。これを1に設定すると、AGVは手動の割り当てポイントで停止し、先の割り当てを行います。p1はAGV_ADD_ALLOC_POINTにより返される割り当てポイントノードへの参照、p2は1または0です。
AGV_ATTACH_TRAILER - AGVに手動でトレーラーを追加します。p1は追加するオブジェクト、p2は適用するトレーラーギャップです。p3が1の場合はトレーラーがAGVの後ろ(AGVの末尾)に追加され、0の場合はトレーラーがAGVの前(AGVの先頭)に追加されます。p4が1の場合、オブジェクトがAGVから出るときにトレーラーが自動的にデタッチされ、0の場合、トレーラーのデタッチは手動で行います。
AGV_DETACH_TRAILER - AGVからトレーラーを手動でデタッチします。p1は、トレーラーとして追加されているオブジェクトです。
AGV_SPEED - AGVの現在の速度を返します。
AGV_PROXIMITY_STATE - AGVが累積パスの近接性によりブロックされている場合は1を、そうでない場合は0を返します。
AGV_ACCUM_AHEAD_AGV - 累積パスで、このAGVの前に別のAGVが存在する場合、そのAGVを返します。
パラメータに応じて、AGVについての各種の情報を取得します。
AGV_CURRENT_CP - AGVの現在のコントロールポイントを返します。
AGV_ORIGIN_CP - AGVの元のコントロールポイントを返します。
AGV_INTERMEDIATE_DEST_CP - AGVの中間目的地コントロールポイントを返します。
AGV_DEST_CP - AGV_INTERMEDIATE_DEST_CPと同じです。
AGV_FINAL_DEST_CP - AGVの最終目的地のコントロールポイントを返します。
AGV_DEST - AGVの目的地オブジェクトを返します。
AGV_BATTERY_LEVEL - AGVの現在のバッテリーレベルをバッテリー容量のパーセンテージ(0~100)で返します。
AGV_AMP_HOURS - AGVの現在のバッテリーレベルをアンペア時で返します。
AGV_START_RECHARGE - AGVの再充電を開始します。最大容量まで再充電するため必要な時間を返します。
AGV_RECHARGE_TO_LEVEL - AGVのバッテリーレベルをp1(0~100)に明示的に設定します。
AGV_ADD_ALLOC_POINT - 移動初期化トリガーから呼び出します。割り当てのコントロールポイント/コントロールエリアを手動で割り当てます。これらは、AGVの現在の移動パスの一部として割り当てる必要がないコントロールポイント/コントロールエリアです。コントロールポイント/コントロールエリアはp1として渡され、どの距離で割り当てる必要があるかがp2として渡されます。このコマンドは、その割り当てを表すノードへの参照を返します。その割り当てポイントについてさらにデータを指定するには、AGV_SET_ALLOC_POINT_DEALLOC_DISTとAGV_SET_CAN_STOP_AT_ALLOC_POINTを使用します。
AGV_SET_ALLOC_POINT_DEALLOC_DIST - 追加された手動の割り当てポイントについて、AGVがオブジェクトを割り当て解除できる移動距離を設定します。オブジェクトが正しく割り当て解除されるよう、割り当ての追加後にいずれかの時点でこのコマンドを呼び出します。p1はAGV_ADD_ALLOC_POINTにより返される割り当てポイントノードへの参照、p2は割り当て解除距離です。
AGV_SET_CAN_STOP_AT_ALLOC_POINT - AGVが、手動で追加された割り当てポイントで停止可能かどうかを設定します。デフォルトはnoで、AGVは停止距離では停止せず、オブジェクトの割り当てを試みる前に次の停止可能なポイントまで続行します。これを1に設定すると、AGVは手動の割り当てポイントで停止し、先の割り当てを行います。p1はAGV_ADD_ALLOC_POINTにより返される割り当てポイントノードへの参照、p2は1または0です。
AGV_ATTACH_TRAILER - AGVに手動でトレーラーを追加します。p1は追加するオブジェクト、p2は適用するトレーラーギャップです。p3が1の場合はトレーラーがAGVの後ろ(AGVの末尾)に追加され、0の場合はトレーラーがAGVの前(AGVの先頭)に追加されます。p4が1の場合、オブジェクトがAGVから出るときにトレーラーが自動的にデタッチされ、0の場合、トレーラーのデタッチは手動で行います。
AGV_DETACH_TRAILER - AGVからトレーラーを手動でデタッチします。p1は、トレーラーとして追加されているオブジェクトです。
AGV_SPEED - AGVの現在の速度を返します。
AGV_PROXIMITY_STATE - AGVが累積パスの近接性によりブロックされている場合は1を、そうでない場合は0を返します。
AGV_ACCUM_AHEAD_AGV - 累積パスで、このAGVの前に別のAGVが存在する場合、そのAGVを返します。
例
agvinfo(agv, AGV_DEST_CP);
agvreassigncp (obj agv, obj controlpoint)
説明
廃止されました。AGVクラスを使用してください。
指定されたコントロールポイントにAGVを再割り当てします。
指定されたコントロールポイントにAGVを再割り当てします。
例
agvreassigncp(agv, controlpoint);
agvredirect (obj agv, obj object/controlpoint, num mode)
説明
廃止されました。AGVクラスを使用してください。
指定されたオブジェクト/コントロールポイントにAGVをリダイレクトします。modeは次のいずれかの値です。
REDIRECT_AND_WAIT - 到着前にリダイレクトされていない場合、AGVはリダイレクトされるまで目的地で待機します。
REDIRECT_AS_FINAL - 目的地がAGVの新しい最終目的地になります。REDIRECT_AND_CONTINUE_ON_ARRIVAL - AGVは中間目的地に到着した後で、最終目的地に移動を続けます。
REDIRECT_AND_CONTINUE_ON_PRE_ARRIVAL - AGVは中間目的地に事前に到着した後で、最終目的地に移動を続けます(減速して停止しません)。
指定されたオブジェクト/コントロールポイントにAGVをリダイレクトします。modeは次のいずれかの値です。
REDIRECT_AND_WAIT - 到着前にリダイレクトされていない場合、AGVはリダイレクトされるまで目的地で待機します。
REDIRECT_AS_FINAL - 目的地がAGVの新しい最終目的地になります。REDIRECT_AND_CONTINUE_ON_ARRIVAL - AGVは中間目的地に到着した後で、最終目的地に移動を続けます。
REDIRECT_AND_CONTINUE_ON_PRE_ARRIVAL - AGVは中間目的地に事前に到着した後で、最終目的地に移動を続けます(減速して停止しません)。
例
agvredirect(agv, controlpoint, 1);
cp (obj/str object_or_name)
説明
AGVコントロールポイントへの参照を返します。
例
cp("CP547");
cpaddlistener (obj rootObj, str connectionPath, node listenerNode, num flags[, ...])
説明
1つ以上のコントロールポイントのイベントに、リスナーを追加します。
例
cpaddlistener(current, "Location > LoadPoints", c, CP_LISTEN_EXIT | CP_LISTEN_AVAILABLE);
cpallocate (obj controlPoint, obj allocator, num force)
説明
要求オブジェクトにコントロールポイントを割り当てます。成功した場合、割り当てを表す結合ノードへの参照が返されます。
例
cpallocate(controlPoint, current, 1);
cpconnection (obj controlpoint/object, num/str connection, num rank)
説明
コントロールポイント接続を返します。また、connectionが文字列で、controlpointとrankの両方が0の場合、このコマンドは与えられた接続のインデックスを返します。このコマンドは、以後のコマンドで接続の番号を使用し迅速化を行うためのものです。
例
cpconnection(cp, "ForwardTo", 1) cpの最初のForwardTo接続を返します。cpconnection(cp, "LookForWork>NextLookForWork", 1) オブジェクトを見つけるため、2つの接続を横断します。これは、cpconnection(cpconnection(cp, "LookForWork", 1), "NextLookForWork", 1) と同じです。cpconnection(cp, "LookForWork:2>NextLookForWork", 1) cpconnection(cpconnection(cp, "LookForWork", 2), "NextLookForWork", 1) と同じです。int connIndex = cpconnection(0, "LookForWork", 0);
treenode obj = cpconnection(cp, connRank, 1); cpdeallocate (obj controlPoint, obj allocator)
説明
要求オブジェクトからコントロールポイントを割り当て解除します。成功した場合は1、失敗した場合は0が返されます。
例
cpdeallocate(controlPoint, current);
cpdistance (obj fromControlPoint, obj toControlPoint)
説明
2つのコントロールポイント間のAGVネットワーク距離を返します。
例
cpdistance(cp1, cp2)
cpisavailable (obj controlpoint)
説明
指定されたコントロールポイントが利用可能な場合、1を返します。byCriterionは現在は使用されず、将来の使用のため予約されています。
例
if (cpisavailable(cp)) {
...
}
...
}
cpnumconnections (obj controlpoint, num/str connection)
説明
コントロールポイントに存在する接続の数を返します。
例
cpnumconnections(cp, "ForwardTo")
cptasksequencequeue (obj controlpoint)
説明
コントロールポイントに関連付けられているタスクシーケンスキューへの参照を返します。
例
treenode tsQueue = cptasksequencequeue(cp);
通信
ソケットなどの外部アプリケーションとの通信、データベース通信、Microsoft Excelとのリンクを行うためのコマンド。
clientclose (num socket)
クライアントソケットを閉じる
説明
このコマンドは、socketで指定されたクライアントソケットを閉じます。
clientcreate()の後、いずれかの時点で呼び出す必要があります。ソケットが閉じると、読み取りや書き込みは一切できなくなります。
ソケット番号は、後でclientcreate()を呼び出すときに再利用できます。この関数は、ソケットが正常に閉じられた場合に真を返します。
clientcreate()の後、いずれかの時点で呼び出す必要があります。ソケットが閉じると、読み取りや書き込みは一切できなくなります。
ソケット番号は、後でclientcreate()を呼び出すときに再利用できます。この関数は、ソケットが正常に閉じられた場合に真を返します。
例
clientclose(1);
clientconnect (num socket, str hostname, num port)
クライアントソケットへの接続を試みる
説明
このコマンドは、socketにより指定されたソケットから、hostnameの名前を持つマシンで実行中の、指定されたポートをリッスンしているサーバーへ接続を試みます。
socketとして渡される数値は、clientcreate()により以前に返された数値です。hostnameとして渡される文字列は、コンピュータの名前(クライアントと同じネットワークに存在する場合)またはIPアドレスです。このコマンドは、clientcreate()呼び出しが成功した後で使用します。ソケットが接続できなかった場合はソケットが閉じ、clientcreate()を再度呼び出して開く必要があります。この関数は、ソケットが正常に接続された場合に真を返します。
socketとして渡される数値は、clientcreate()により以前に返された数値です。hostnameとして渡される文字列は、コンピュータの名前(クライアントと同じネットワークに存在する場合)またはIPアドレスです。このコマンドは、clientcreate()呼び出しが成功した後で使用します。ソケットが接続できなかった場合はソケットが閉じ、clientcreate()を再度呼び出して開く必要があります。この関数は、ソケットが正常に接続された場合に真を返します。
例
clientconnect(1,"localhost",1880);
clientcreate ()
TCP/IPプロトコルで新規クライアントソケットを作成する
説明
このコマンドは、TCP/IPプロトコルで通信を行うように設定された、新しいクライアントソケットを作成します。FlexSimは、同時に50までのクライアントソケットを作成できます。
各クライアントは、別のサーバーに接続できます。この関数は数値を返し、モデルは作成されたソケットを参照するために数値を保存する必要があります。
エラーが発生した場合、この関数は0を返します。
各クライアントは、別のサーバーに接続できます。この関数は数値を返し、モデルは作成されたソケットを参照するために数値を保存する必要があります。
エラーが発生した場合、この関数は0を返します。
例
int socknum = clientcreate();
clientreceive (num socket, str buffer, num buffersize, num noblock[1/0])
ソケットへ送信されたデータを受信する
説明
このコマンドは、socketで指定されるソケットに送信されたデータを受信します。socketの値は、clientcreate()により返された数値です。このコマンドは、flexscriptとc++で動作が異なります。c++では、bufferはchar*デスティネーションへの有効なポインターの必要があり、読み取られたバイトはこのバッファにコピーされます。戻り値は、受信した合計バイト数です。クライアントのメッセージから最大でbufsizeまでのバイトが読み取られ、bufという名前の事前に割り当てられた文字配列に格納されます。これに対してflexscriptでは、bufferにNULLを渡し、戻り値は受信された実際の文字列です。noblocking = 1のとき、このコマンドはFlexSimプログラムの実行をブロックしません。noblocking = 0のとき、クライアントから何かが受信されるまでFlexSimプログラムの実行はブロック(フリーズ)されます。
例
c++: int bytes = clientreceive(1,Buf,15,0);
flexscript: string readstr = clientreceive(1, NULL, 15, 0);
flexscript: string readstr = clientreceive(1, NULL, 15, 0);
clientsend (num socket, str message[, num charlength])
ソケットからメッセージを送信する
説明
このコマンドは、socketで指定されるソケットからメッセージを送信します。socketとして渡される数値は、clientcreate()により返された数値です。charlengthは渡される文字列の長さで、通常は省略可能です。送信される文字列にNULL文字が含まれている場合のみ必須となります。
例
clientsend(1,"REQ:service");
dbchangetable (str tablename)
ODBCデータベースに、tablenameで指定される名前のテーブルを開く
説明
このコマンドは、tablenameで指定される名前のテーブルをデータベースに開きます。データベースがSQLモードで開いている場合、このコマンドは何もしません。このコマンドが呼び出されたとき開いていたテーブルは閉じられます。新しいテーブルのみが読み取り可能です。これにより、ユーザーはデータベース全体を閉じて再度開く必要なしに、テーブルモードで複数のテーブルを読み取ることができます。
例
dbchangetable("Inventory");
現在開いているテーブルを閉じ、Inventoryという名前のテーブルを開きます。
現在開いているテーブルを閉じ、Inventoryという名前のテーブルを開きます。
dbclose ()
現在開いているODBCデータベースを閉じる
説明
このコマンドは、現在開いているODBCデータベースを閉じます。同時に開くことのできるデータベースは1つだけです。このコマンドは、dbopen()よりも前に呼び出された場合は何も行いません。SQLの「INSERT」コマンドの後に呼び出されると、エラーメッセージが返されます。dbclose()を呼び出す前に、通常の「SELECT」ステートメントを使用してください。
例
if (current.donegatheringdata == 1)
dbclose();
ラベルdonegatheringdataが現在1に設定されていれば、現在のデータベースが閉じられます。
dbclose();
ラベルdonegatheringdataが現在1に設定されていれば、現在のデータベースが閉じられます。
dbexportnode (obj tablenode, num startrow, num startcol, num numrows, num numcols)
説明
指定されたノードから始まるテーブルを、現在開いているデータベーステーブルにエクスポートします。
テーブルの開始の行と列、およびエクスポートする行と列の数を指定します。
テーブルの開始の行と列、およびエクスポートする行と列の数を指定します。
例
dbexportnode(so(),1,1,4,5);
dbexporttable (str tablename, num startrow, num startcol, num numrows, num numcols)
グローバルテーブルtablenameを、現在開いているODBCテーブルにエクスポートする
説明
指定されたグローバルテーブルを、現在開いているデータベーステーブルにエクスポートします。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
例
dbexportnode("MyTable4",2,2,3,3);
dbgetfieldname (num column)
開いているODBCデータベースのフィールド名を取得する
説明
このコマンドは、現在開いているODBCデータベースで、fieldnumにより指定されるフィールドまたは列の名前を返します。データベースが現在開いていない場合、空の文字列が返されます。存在しないフィールド番号を指定すると、例外が発生します。
例
string ColName = dbgetfieldname(1);
現在のデータベースにある最初の列の名前を、ColNameに設定します。
現在のデータベースにある最初の列の名前を、ColNameに設定します。
dbgetmetrics ()
開いているODBCデータベースのテーブルの寸法を取得する
説明
開いているODBCデータベースのテーブルの寸法を取得します。
例
dbgetmetrics()
dbgetmode ()
開いているODBCデータベースの現在のモードを取得する
説明
このコマンドは、現在開いているODBCデータベースのモードを返します。戻り値は次のとおりです。
DBMODE_CLOSED - 0 - データベースが開いていない
DBMODE_SQL - 1 - データベースがSQLモードで開いている
DBMODE_TABLE - 2 - データベースがテーブルモードで開いている
DBMODE_CLOSED - 0 - データベースが開いていない
DBMODE_SQL - 1 - データベースがSQLモードで開いている
DBMODE_TABLE - 2 - データベースがテーブルモードで開いている
例
if (dbgetmode() != DBMODE_CLOSED)
ColName = dbgetfieldname(1);
データベースが開いていれば、データベースにある最初の列の名前が、ColNameに設定されます。
ColName = dbgetfieldname(1);
データベースが開いていれば、データベースにある最初の列の名前が、ColNameに設定されます。
dbgetnumcols ()
開いているODBCデータベースの列数を取得する
説明
このコマンドは、現在開いているODBCデータベースの列数を返します。データベースが開いていなければ、0が返されます。
例
for (int x=1; x<=dbgetnumcols(); x++)
Table("MyTable")[1][x] = stringtonum(dbgettablecell(1,x));
データベースの列の値を、GlobalTableの列にコピーします。
Table("MyTable")[1][x] = stringtonum(dbgettablecell(1,x));
データベースの列の値を、GlobalTableの列にコピーします。
dbgetnumrows ()
開いているODBCデータベースの行数を取得する
説明
このコマンドは、現在開いているODBCデータベースの行数を返します。データベースが開いていなければ、0が返されます。
例
for (int x=1; x<=dbgetnumrows(); x++)
Table("MyTable")[x][1] = stringtonum(dbgettablecell(x,1));
データベースの行の値を、GlobalTableの行にコピーします。
Table("MyTable")[x][1] = stringtonum(dbgettablecell(x,1));
データベースの行の値を、GlobalTableの行にコピーします。
dbgettablecell (num row, num col)
開いているODBCデータベースのrowおよびcolと関連付けられている文字列を取得する
説明
このコマンドは、現在開いているODBCデータベースでrowおよびcolにより指定されるセルの情報を含む文字列を返します。データベースが開いていない場合、この関数はnull文字列(値0)を返します。
例
double tablevalue = stringtonum(dbgettablecell(1,1));
tablevalueを、データベースの最初の行、最初の列に格納されている数値に設定します。
tablevalueを、データベースの最初の行、最初の列に格納されている数値に設定します。
dbgettablenum (num row, num col)
現在開いているODBCテーブルの行、列の数値を取得する
説明
現在のデータベーステーブルで、指定されたrowおよびcolにある数値を返します。
例
double val = dbgettablenum(2,3);
dbgettablestr (num row, num col)
現在開いているODBCテーブルの行、列の文字列を取得する
説明
現在のデータベーステーブルで、指定された行および列にある文字列を返します。
注意:FlexScriptのみのフィールドで使用された場合は数値が返され、tostring()を使用して明示的に文字列に変換する必要があります。
注意:FlexScriptのみのフィールドで使用された場合は数値が返され、tostring()を使用して明示的に文字列に変換する必要があります。
例
string val = dbgettablenum(2,3);
dbimportnode (obj tablenode, num startrow, num startcol, num numrows, num numcols)
現在開いているODBCテーブルからtablenodeにインポートする
説明
現在開いているデータベーステーブルを、指定されたノードから始まるテーブルにインポートします。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
例
dbimportnode(so(),1,1,4,5);
dbimporttable (str tablename, num startrow, num startcol, num numrows, num numcols)
現在開いているODBCテーブルからグローバルテーブルtablenameにインポートする
説明
現在開いているデータベーステーブルを、指定されたグローバルテーブルにインポートします。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
テーブルの開始の行と列、およびインポートする行と列の数を指定します。
例
dbimportnode("MyTable4",2,2,3,3);
dbopen (str databasename, str command {SQL string or Tablename}, num usetable [, num showlogin])
ODBCデータベースを開く
説明
このコマンドは、ODBCデータベースを開く動作を試みます。成功した場合は1、失敗した場合は0が返されます。データベースを開く前に、ODBCエイリアス(またはデータソース名DSN)が定義されている必要があります。この操作は、Windowsコントロールパネルの[データソース]オプションを使用して行います。エイリアス名はdatabasenameとしてコマンドに渡されます。データベースのファイル名は渡しません。データベースは2つの異なるモードで開くことができます。これらのモードは、動作および使用可能なコマンドが多少異なります。SQLモードとテーブルモードがあります。パラメータtablemodeが1ならデータベースはテーブルモードで開き、commandには開くデータベースのテーブル名を使用します。テーブルが正しく開かれると、テーブル全体を読み取れるようになります。テーブルモードでは各セルを編集できます。データベースがテーブルモードのとき、SQLコマンドは呼び出せません。tablemodeが0ならデータベースはSQLモードで開き、commandには最初のSQLクエリを使用します。クエリが正しく実行されると、クエリの結果のみを読み取ることができます。SQLモードでは各セルを編集できません。ただし、データベースが開くとSQL更新クエリを呼び出すことができます。showloginが1なら、データベースへの接続を行う前に標準のログインプロンプト(ユーザー名/パスワード)が表示されます。
例
dbopen("itemdrive","timetable",1);
データベースをエイリアス「itemdrive」で開き、「timetable」という名前のテーブルをテーブルモードで開きます。
dbopen("warehouse","select * from inventory",0);
データベースをエイリアス「warehouse」で開き、SQLクエリを実行します。データベースはSQLモードで開きます。
データベースをエイリアス「itemdrive」で開き、「timetable」という名前のテーブルをテーブルモードで開きます。
dbopen("warehouse","select * from inventory",0);
データベースをエイリアス「warehouse」で開き、SQLクエリを実行します。データベースはSQLモードで開きます。
dbsettablecell (num row, num col, str value)
開いているODBCデータベースの行、セルの値を設定する
説明
このコマンドは、現在開いているODBCデータベースで、rowおよびcolで指定されるセルの値をvalueに設定します。データベースがSQLモードで開いている場合、このコマンドは何もしません。データベースのエイリアスが読み取り専用に設定されている場合、このコマンドは例外を引き起こします。エイリアスは、Windowsコントロールパネルの[データソース]オプションで読み取り専用に設定されます。関数に数値を渡す必要がある場合は、strintonum()コマンドを使用します。
例
for (int x=1; x<= model().subnodes.length; x++)
dbsettablecell(x,1,model().subnodes[x].name);
モデルのすべてのオブジェクトの名前を、現在のデータベースの最初の列に置きます。
dbsettablecell(x,1,model().subnodes[x].name);
モデルのすべてのオブジェクトの名前を、現在のデータベースの最初の列に置きます。
dbsettablenum (num row, num col, num val)
現在開いているODBCテーブルのrowおよびcolの数値を設定する
説明
現在のデータベーステーブルで、指定されたrowおよびcolの値を、与えられた数値に設定します。
例
dbsettablenum(2,3,56.5);
dbsettablestr (num row, num col, str val)
現在開いているODBCテーブルの行、列に文字列を設定する
説明
現在のデータベーステーブルで、指定されたrowおよびcolの値を、与えられた文字列に設定します。
例
dbgettablestr(1,1,"John");
dbsqlquery (str query[, num forwardOnlyCursor])
開いているODBCデータベースにSQLクエリを実行する
説明
このコマンドは、現在開いているデータベースに対して、queryにより指定されたSQLクエリを実行します。結果は現在のテーブルとなります。データベースがテーブルモードのとき、このコマンドは何もしません。クエリによりテーブルが返された場合、dbgettablecell()コマンドを使用してテーブルを読み取ることができます。クエリにより更新が行われた場合、dbgettablecell()コマンドを実行すると例外が引き起こされます。
このコマンドでUPDATEステートメントを実行した場合はテーブルが返されないため、直後にSELECTを呼び出します。このコマンドはSQLモードでのみ使用できます。forwardOnlyCursorが1の場合、結果は順方向のみのカーソルの結果と想定されます。順方向のみのカーソルにはdbgetnumrows()を使用できません。その代わりに、dbsqlquery()の後でdbnextrow()を呼び出してください。このコマンドはアクティブ化された行を返します。テーブルの末尾に到達すると、-1を返します。
このコマンドでUPDATEステートメントを実行した場合はテーブルが返されないため、直後にSELECTを呼び出します。このコマンドはSQLモードでのみ使用できます。forwardOnlyCursorが1の場合、結果は順方向のみのカーソルの結果と想定されます。順方向のみのカーソルにはdbgetnumrows()を使用できません。その代わりに、dbsqlquery()の後でdbnextrow()を呼び出してください。このコマンドはアクティブ化された行を返します。テーブルの末尾に到達すると、-1を返します。
例
dbsqlquery("select processtime from timetable where type='1'");
渡されたSQLクエリに基づく新しいテーブルを返します。
dbsqlquery("update timetable set processtime=type*2");
渡されたクエリに基づいてデータベースを更新します。
渡されたSQLクエリに基づく新しいテーブルを返します。
dbsqlquery("update timetable set processtime=type*2");
渡されたクエリに基づいてデータベースを更新します。
dbusername (str username, str password)
dbopen()でODBCデータベースにアクセスするため使用するユーザー名とパスワードを設定する
説明
このコマンドは、次にdbopen()を呼び出すときデータベースにアクセスするため使用する、ユーザー名とパスワードを設定します。これにより、モデル作成者はdbopen()で提供されるユーザー名とパスワードのプロンプトを使用せず、データベースに要求されるログインパラメータを使用できます。このコマンドで設定されるユーザー名とパスワードは、再度dbusername()を呼び出して変更されるまで、dbopen()呼び出しのたびに使用されます。ユーザー名、パスワード、または両方を空の文字列に設定することもできます。
例
dbusername("user1","abc123XYZ");
ユーザー名を「user1」、パスワードを「abc123XYZ」に設定します。これらの値は、次にdbopen()が呼び出されるときデータベースにアクセスするため使用されます。
dbusername("","");
最後に設定したユーザー名とパスワードをクリアします。dbopen()が次に呼び出されたとき、データベースはユーザー名とパスワードなしでアクセスされます。
ユーザー名を「user1」、パスワードを「abc123XYZ」に設定します。これらの値は、次にdbopen()が呼び出されるときデータベースにアクセスするため使用されます。
dbusername("","");
最後に設定したユーザー名とパスワードをクリアします。dbopen()が次に呼び出されたとき、データベースはユーザー名とパスワードなしでアクセスされます。
dbviewtable ()
読み取り専用ダイアログボックスを開き、現在ロードされているODBCテーブルを表示する
説明
ダイアログボックスを開き、現在ロードされているデータベーステーブルを表示します。このダイアログからはテーブルを編集できません。
例
dbviewtable();
excelclose (num save [1/0])
現在開いているExcelワークブックを閉じる
説明
このコマンドは、現在開いているExcelワークブックを閉じます。saveが1なら、ワークブックは閉じる前に保存されます。saveが0なら、ワークブックに加えられた変更内容は破棄されます。
例
excelopen()の例を参照してください。
excelcreatesheet (str name)
現在開いているExcelワークブックに新しいワークシートを作成します。
説明
新しいワークシートを作成します。新しいシートにはnameで指定した名前が付けられます。
例
excelcreatesheet("MyNewSheet");
excelcreateworkbook ()
Excelワークブックを作成する
説明
このコマンドは、Excelでワークブックを作成します。同時に開くことのできるワークブックは1つだけです。ユーザーは、別のワークブックを開くまたは作成する、新しいモデルを開く、現在のモデルをコンパイルする、またはFlexSimを閉じる前に、excelclose()を呼び出す必要があります。開いているファイルから読み取りを行う前には、excelsetsheet()も呼び出す必要があります。
例
excelcreateworkbook();
excelsetsheet("Sheet1");
excelwritenum(1,1,1);
excelsave("NewWorkBook.xlsx");
excelclose(0);
最初にFlexSimと新しいExcelワークブックとの間にリンクを作成し、ワークブックのアクティブなシートを「Sheet1」に設定し、行1列1に1を書き込み、ワークブックを保存して、ワークブックを閉じます。
excelsetsheet("Sheet1");
excelwritenum(1,1,1);
excelsave("NewWorkBook.xlsx");
excelclose(0);
最初にFlexSimと新しいExcelワークブックとの間にリンクを作成し、ワークブックのアクティブなシートを「Sheet1」に設定し、行1列1に1を書き込み、ワークブックを保存して、ワークブックを閉じます。
exceldeleterange (str rangename)
現在開いているExcelワークブックの指定範囲を削除します。
説明
指定範囲を削除します。範囲内のデータには影響しません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
exceldeleterange("MyRange");
exceldeletesheet (str name [, int allowwarning])
現在開いているExcelワークブックのワークシートを削除します。
説明
指定されたワークシートを削除します。allowwarningが1なら、データのあるシートを削除する前に警告が与えられます。
例
exceldeletesheet("MyNewSheet");
excelexporttable (str/node/num table, num startrow, num startcol, num numrows, num numcols [, num rowchar, num colchar])
FlexSim内のテーブルから、現在開いているExcelワークブックにデータをエクスポートする
説明
FlexSim内のテーブルから、Excelにデータをエクスポートします。テーブルはGlobalTableの名前で参照することも、テーブルノードへのツリーノード参照を使用することもできます。エクスポートされるデータタイプ(文字列または数値)は、FlexSimテーブルのセルのデータタイプにより決定されます。ユーザーは、Excelの開始行および列番号と、エクスポートする行および列の総数を指定します。
例
excelexporttable("Table1",1,1,5,3);
excelgetrangeparam (str rangename, num param)
現在開いているExcelワークブックの名前付き範囲についての位置パラメータを取得する
説明
名前付き範囲についての位置パラメータを取得します。パラメータの有効な値は次のとおりです。
1 = 開始行番号
2 = 開始列番号
3 = 終了行番号
4 = 終了列番号
5 = 幅
6 = 高さ
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
1 = 開始行番号
2 = 開始列番号
3 = 終了行番号
4 = 終了列番号
5 = 幅
6 = 高さ
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
int width = excelgetrangeparam("MyRange",5);
excelgetrangesheet (str rangename)
現在開いているExcelワークブックのrangenameと関連付けられているワークシートの名前を取得する
説明
指定された範囲が位置するワークシートの名前を返します。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
pt(excelgetrangesheet("MyRange"));
excelimporttable (str/node/num table, num startrow, num startcol, num numrows, num numcols)
現在開いているExcelワークブックから、FlexSimのテーブルにデータをインポートします。
説明
Excelから、FlexSimのテーブルにデータをインポートします。テーブルはGlobalTableの名前で参照することも、テーブルノードへのツリーノード参照を使用することもできます。エクスポートされるデータタイプ(文字列または数値)は、FlexSimテーブルのセルのデータタイプにより決定されます。ユーザーは、Excelの開始行および列番号と、エクスポートする行および列の総数を指定します。
例
excelimporttable("MyTable",1,1,5,3);
excellaunch ([str launchdir])
Microsoft Excelを開始する
説明
このコマンドは、Microsoft Excelを開き、FlexSimからアクセスできるようにします。launchdirが指定されていない場合、[ツール]|[Excel]|[グローバル設定]で定義されているパスが使用されます。それ以外の場合、launchdirはハードドライブ上でEXCEL.EXEが置かれている場所を指す正確なパスである必要があります。一般には"C:/Program Files/Microsoft Office/Office10"のような形式ですが、インストールされているExcelのバージョンによって異なる可能性があります。通常、Excelとの通信を行う前にExcelを開始する必要はありません。ただし、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(デフォルト動作ではなく、maintenance(1000,1)を呼び出して)場合は、通信を行う前にExcelが実行されている必要があります。通信の開始時にexcellaunch()を呼び出しれた場合、ユーザーが新しいモデルを開く、現在のモデルをコンパイルする、またはFlexSimを閉じる前に、excelquit()を呼び出す必要があります。
例
excellaunch("C:/Program Files/Microsoft Office/Office10");
excelopen("C:/mybook.xls");
excelsetsheet("Sheet1");
double thenum = excelreadnum(1,1);
excelclose(true);
excelquit();
Excelを開始し、「mybook」という名前のワークブックを開き、そのワークブックの行1、列1から読み取った値を保存して、ファイルとExcelを閉じます。
excelopen("C:/mybook.xls");
excelsetsheet("Sheet1");
double thenum = excelreadnum(1,1);
excelclose(true);
excelquit();
Excelを開始し、「mybook」という名前のワークブックを開き、そのワークブックの行1、列1から読み取った値を保存して、ファイルとExcelを閉じます。
excelmultitableimport ()
ExcelからFlexSimテーブルにデータの自動インポートを開始する
説明
[ツール]|[Excel]|[複数テーブルのインポート]ウィンドウでのセットアップに従い、ExcelシートからFlexSimテーブルにデータの自動インポートを開始します。
例
excelmultitableimport()
excelopen (str workbook)
Excelワークブックを開く
説明
このコマンドは、workbookで指定される名前のファイルをExcelで開きます。同時に開くことのできるワークブックは1つだけです。ユーザーは、別のワークブックを開く、新しいモデルを開く、現在のモデルをコンパイルする、またはFlexSimを閉じる前に、excelclose()を呼び出す必要があります。開いているファイルから読み取りを行う前には、excelsetsheet()も呼び出す必要があります。
例
excelopen("mydata.xls");
excelsetsheet("Sheet1");
double myvalue = excelreadnum(1,2);
excelclose(0);
最初にFlexSimと、「mydata.xls」という名前のExcelワークブックとの間にリンクを作成し、ワークブックのアクティブなシートを「Sheet1」に設定し、行1列2から読み取られた数値をmyvalueという名前のローカル変数に設定して、保存せずにワークブックを閉じます。
excelsetsheet("Sheet1");
double myvalue = excelreadnum(1,2);
excelclose(0);
最初にFlexSimと、「mydata.xls」という名前のExcelワークブックとの間にリンクを作成し、ワークブックのアクティブなシートを「Sheet1」に設定し、行1列2から読み取られた数値をmyvalueという名前のローカル変数に設定して、保存せずにワークブックを閉じます。
excelquit ()
Microsoft Excelを閉じる
説明
このコマンドは、Microsoft Excelが開いていれば、閉じます。このコマンドを呼び出した後は、Excelへの他のコマンドは呼び出せません。開いているExcelファイルは、このコマンドを呼び出す前に閉じる必要があります。開いているワークブックについて、変更の保存を求めるExcelプロンプトが表示されることがあります。これを回避するにはexcelclose()を使用します。以前にexcellaunch()を呼び出した場合、このコマンドを呼び出す必要があります。
例
excellaunch()を参照してください。
excelrangereadnum (str rangename, num row, num column)
現在開いているExcelワークブックの指定範囲のセルから数値を読み取る
説明
指定された名前付き範囲の、行および列により定義されたセルから数値を読み取ります。範囲の左上のセルが行1、列1です。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
excelreadnum("MyRange",5,1)
excelrangereadstr (str rangename, num row, num column [, num rowchar, num colchar])
現在開いているExcelワークブックの指定範囲のセルからテキスト値を読み取る
説明
指定された名前付き範囲の、rowおよびcolumnにより定義されたセルからテキスト値を読み取ります。範囲の左上のセルが行1、列1です。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
excelreadstr("MyRange",5,1)
excelrangewritenum (str rangename, num row, num column, num value)
現在開いているExcelワークブックの指定範囲のセルに数値を書き込む
説明
指定された名前付き範囲の、rowおよびcolumnにより定義されたセルに数値を書き込みます。範囲の左上のセルが行1、列1です。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。テーブル全体の値をExcelに書き込むには、excelrangewriteを使用します。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。テーブル全体の値をExcelに書き込むには、excelrangewriteを使用します。
例
excelwritenum("MyRange",5,1,99.87)
excelrangewritestr (str rangename, num row, num column, str value)
現在開いているExcelワークブックの指定範囲のセルに文字列値を書き込む
説明
指定された名前付き範囲の、rowおよびcolumnにより定義されたセルに文字列値を書き込みます。範囲の左上のセルが行1、列1です。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。テーブル全体の値をExcelに書き込むには、excelrangewriteを使用します。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。テーブル全体の値をExcelに書き込むには、excelrangewriteを使用します。
例
excelwritestr("MyRange",5,1,"My String")
excelreadcell (num row, num col[, num flags])
アクティブなワークシートのセルの値をバリアントとして返す
説明
アクティブなワークシートのセルの値をバリアントとして返します。Excelから何を返すかを正確に指定するため、flagsを指定できます。使用できるフラグはEXCEL_DATA_NUMBER、EXCEL_DATA_STRING、EXCEL_DATE_AS_NUMです。
EXCEL_DATA_NUMBERは、Excelデータを数値として読み取ります。
EXCEL_DATA_STRINGは、Excelデータを文字列として読み取ります。
EXCEL_DATE_AS_NUMは、Excelの日付をFlexsimで読み取り可能な日付数値として解釈します。
EXCEL_DATA_NUMBERは、Excelデータを数値として読み取ります。
EXCEL_DATA_STRINGは、Excelデータを文字列として読み取ります。
EXCEL_DATE_AS_NUMは、Excelの日付をFlexsimで読み取り可能な日付数値として解釈します。
例
Variant value = excelreadcell(1, 5, EXCEL_DATA_NUMBER | EXCEL_DATE_AS_NUM);
最初の行に含まれる5つの列の値を数値として返します。その値が日付の場合、Flexsimで日付として読み取り可能な数値が返されます。
最初の行に含まれる5つの列の値を数値として返します。その値が日付の場合、Flexsimで日付として読み取り可能な数値が返されます。
excelreadnum (num row, num column [, num rowchar, num colchar])
現在開いているExcelワークブックのアクティブなシートのセルから数値を読み取る
説明
現在開いているExcelワークブックのアクティブなシートのrowおよびcolumnで定義されるセルから、数値を読み取ります。
例
excelreadnum(5,1)
excelreadstr (num row, num column [, num rowchar, num colchar])
現在開いているExcelワークブックのアクティブなシートのセルからテキスト値を読み取る
説明
現在開いているExcelワークブックのアクティブなシートのrowおよびcolumnで定義されるセルから、テキスト値を読み取ります。
例
excelreadstr(5,1)
excelsave ([str filename])
現在開いているExcelファイルを保存する
説明
現在開いているExcelファイルを保存します。このコマンドにfilenameが渡された場合、その名前でファイルが保存されます。これは、Excelの[ファイル]メニューで[名前を付けて保存]を選択するのと同じです。このコマンドにパラメータが渡されない場合、ファイルは現在の名前で保存され、元のファイルが上書きされます。これは、Excelの[ファイル]メニューで[上書き保存]を選択するのと同じです。
例
excelsave("runresults_001.xls")
excelsetrange (str rangename, num startrow, num startcolumn, num endrow, num endcolumn)
現在開いているExcelワークブックの名前付き範囲を作成または変更する
説明
名前付き範囲を作成または変更します。この範囲はアクティブなシート上のものです。範囲の左上のセルがstartrowとstartcolumnにより定義されます。右下のセルはendrowとendcolumnにより定義されます。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
このコマンドは、FlexSimがDDEを使用してExcelと通信を行うよう設定されている(FlexSimのデフォルト設定ではなく、maintenance(1000,1)を呼び出して)場合は何もしません。
例
excelsetrange("MyRange",5,5,10,15);
excelsetsheet (str sheetname)
現在開いているExcelワークブックのアクティブなワークシートの設定
説明
このコマンドは、現在開いているExcelワークブックのアクティブなワークシートを設定します。excelreadnum()またはexcelreadstr()が呼び出されるたびに、値はアクティブなワークシートから読み取られます。開いている同一のワークブックについて、アクティブなワークシートは何回でも設定できます。
例
excelopen()の例を参照してください。
excelversion ()
Microsoft Excelのバージョンを取得する
説明
Excelインターフェイスのバージョンを含む文字列を返します。
例
excelversion()
excelwritenum (num row, num column, num value [, num rowchar, num colchar])
現在開いているExcelワークブックのアクティブなシートのセルに数値を書き込む
説明
現在開いているExcelワークブックのアクティブなシートのrowおよびcolumnで定義されるセルに、数値を書き込みます。
例
excelwritenum(5,1,99.87)
excelwritestr (num row, num column, str value [, num rowchar, num colchar])
現在開いているExcelワークブックのアクティブなシートのセルに文字列値を書き込む
説明
現在開いているExcelワークブックのアクティブなシートのrowおよびcolumnで定義されるセルに、文字列値を書き込みます。
例
excelwritestr(5,1,"My String")
rundocument (str command, str path+filename)
ファイルタイプのデフォルトのアプリケーションを使用してファイルを開く
説明
指定された拡張子のファイルを、そのコンピュータでデフォルトのアプリケーションを使用して開きます。使用可能なコマンドはedit、explore、find、open、printです。戻り値が32より大きい場合は成功を意味します。
例
rundocument("open","C:/myfile.doc");
myfile.docを、コンピュータで*.docファイルを開くためのデフォルトのアプリケーションで開きます。
myfile.docを、コンピュータで*.docファイルを開くためのデフォルトのアプリケーションで開きます。
runprogram (str commandline)
外部プログラムを実行する
説明
外部プログラムを実行します。このコマンドは、オペレーティングシステムにコマンドを発行します。コマンドラインにはプログラムの完全な引数を含めることができます。戻り値が31より大きい場合は成功を意味します。
例
runprogram("c:/myprogram.exe")
serveraccept (int noblocking)
サーバーでクライアント接続の受け付けを試みる
説明
サーバーで、クライアント接続の受け付けを試みます。noblocking = 0なら、このコマンドは接続が作成されるまでブロックを行います。作成された接続への参照に使用されるインデックスが返されます。
サーバーは、待機中のクライアントから接続の受け付けを試みます。確立された接続のインデックスが数値として返されます。戻り値が0の場合、接続が作成されなかったことを示します。この値は、以後のすべてのサーバー呼び出しで使用されます。noblocking = 1なら、サーバーはFlexSimプログラムの実行をブロックしませんが、クライアントが接続を試みなかった場合に0を返します。noblocking = 0なら、サーバーはクライアントが接続を試みるまでFlexSimプログラムの実行をブロック(フリーズ)します。クライアントとの接続を作成するのはこのコマンドのみです。
サーバーは、待機中のクライアントから接続の受け付けを試みます。確立された接続のインデックスが数値として返されます。戻り値が0の場合、接続が作成されなかったことを示します。この値は、以後のすべてのサーバー呼び出しで使用されます。noblocking = 1なら、サーバーはFlexSimプログラムの実行をブロックしませんが、クライアントが接続を試みなかった場合に0を返します。noblocking = 0なら、サーバーはクライアントが接続を試みるまでFlexSimプログラムの実行をブロック(フリーズ)します。クライアントとの接続を作成するのはこのコマンドのみです。
例
int client = serveraccept(0);
servercloseconnection (int connection)
クライアント接続を閉じる
説明
クライアントへの指定された接続を閉じます。メインサーバーソケットは閉じられません。サーバーがクライアントとの通信を完全に終了したとき、このコマンドを使用します。
例
servercloseconnection(1);
serverclosemain ()
メインサーバーソケットと、開いているすべての接続を閉じる
説明
メインサーバーソケットと、まだ開いているすべての接続を閉じます。再度接続が作成されるまで、以後の通信は行われません。このコマンドを呼び出す前に、すべての接続を閉じてください。
例
serverclosemain()
servercreatemain (int port)
指定のポートへの接続をリッスンするサーバーソケットを作成する
説明
指定のポートでの接続をリッスンするサーバーソケットを作成します。一部のポート(既知のポートと呼ばれます)は、特別なアプリケーション用に予約されています。通常、1024より大きい番号のポートはすべて安全に使用できます。
例
servercreatemain(1880);
serverreceive (int connection, char *buffer, int bufsize, int noblocking)
接続からメッセージを受信する
説明
指定の接続からメッセージを受信します。このコマンドは、flexscriptとc++で動作が異なります。c++では、bufferはchar*デスティネーションへの有効なポインターの必要があり、読み取られたバイトはこのバッファにコピーされます。戻り値は、受信した合計バイト数です。クライアントのメッセージから最大でbufsizeまでのバイトが読み取られ、bufという名前の事前に割り当てられた文字配列に格納されます。これに対してflexscriptでは、bufferにNULLを渡し、戻り値は受信された実際の文字列です。noblocking = 1のとき、このコマンドはFlexSimプログラムの実行をブロックしません。noblocking = 0のとき、クライアントから何かが受信されるまでFlexSimプログラムの実行はブロック(フリーズ)されます。
例
c++: int bytes = serverreceive(1,Buf,15,0);
flexscript: string readstr = serverreceive(1, NULL, 15, 0);
flexscript: string readstr = serverreceive(1, NULL, 15, 0);
serversend (int connection, char* message [, num charlength] )
クライアント接続から接続にメッセージを送信する
説明
指定された接続に接続されているクライアントへ、指定のテキストメッセージを送信します。正しく送信されたバイト(文字)数が返されます。送信するテキストメッセージは、char*に変換する必要があります。charlengthは渡される文字列の長さで、通常は省略可能です。送信される文字列にNULL文字が含まれている場合のみ必須となります。
例
serversend(1,"MadeConnection");
socketend ()
socketinit()で開始されたプロセスをシャットダウンする
説明
このコマンドは、socketinit()で開始されたプロセスをシャットダウンします。モデルが、開いたソケットでの作業を完全に終了したとき、このコマンドを呼び出します。この関数は、ソケットが正常にシャットダウンされた場合に真を返します。詳細については、clientsend()を参照してください。
例
socketend();
socketinit ()
Windows Socketsを使用可能にするバックグラウンドプロセスを初期化する
説明
このコマンドは、Windows Socketsを使用可能にするバックグラウンドプロセスを初期化します。ソケットコマンドの呼び出しを行う前に呼び出す必要があります。この関数は、初期化が成功した場合に真を返します。詳細については、clientsend()を参照してください。
例
socketinit();
変換
単位、データタイプ、空間座標を変換するコマンド。
apchar (str string)
文字列とchar*としてアサートする
説明
タイプをC形式の文字列(例:char*)としてアサートします。stringtopcharのエイリアスです。
例
apchar("hello")
cm (num centimeters)
センチメートル単位の数値をメートル単位の数値に変換する
説明
指定されたセンチメートル単位の数値に対応する、メートル単位の数値を返します。
例
cm(3)
convert (var value, var from, var to)
指定された値(時間)を、ある時間形式から別の時間形式に変換する
説明
指定された値(時間)を、ある時間形式から別の時間形式に変換します。fromおよびto引数には、次の値のみを使用できます。
FS_DATETIME
XL_DATETIME
MODEL_TIME
DATE_STR
TIME_STR
DATETIME_STR
FS_DATETIME - 1601年1月1日から計算した秒数。getmodelunit(START_TIME)はFS_DATETIME単位で数値を返します。
XL_DATETIME - 1900年1月1日を1として順に計算した日数。2025年2月10日、午後1時30分は、XL_DATETIME単位では45698.5625です。この形式は、Microsoft Excelで日付に使用されます。
MODEL_TIME - モデル開始時間から後のモデル単位数。
DATE_STR - datetime値の日付部分を表す文字列。結果として得られるテキストは、モデル設定で指定された日付形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。
TIME_STR - datetime値の時刻部分を表す文字列。結果として得られるテキストは、モデル設定で指定された時刻形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。
DATETIME_STR - datetime値の日付と時刻の部分を表す文字列。結果として得られるテキストは、モデル設定で指定された日時と時刻の形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。時刻部分が先で、1つのスペースによって日付部分と区切る必要があります。
このコマンドでは、3000年およびそれ以後はサポートされないことに注意してください。
FS_DATETIME
XL_DATETIME
MODEL_TIME
DATE_STR
TIME_STR
DATETIME_STR
FS_DATETIME - 1601年1月1日から計算した秒数。getmodelunit(START_TIME)はFS_DATETIME単位で数値を返します。
XL_DATETIME - 1900年1月1日を1として順に計算した日数。2025年2月10日、午後1時30分は、XL_DATETIME単位では45698.5625です。この形式は、Microsoft Excelで日付に使用されます。
MODEL_TIME - モデル開始時間から後のモデル単位数。
DATE_STR - datetime値の日付部分を表す文字列。結果として得られるテキストは、モデル設定で指定された日付形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。
TIME_STR - datetime値の時刻部分を表す文字列。結果として得られるテキストは、モデル設定で指定された時刻形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。
DATETIME_STR - datetime値の日付と時刻の部分を表す文字列。結果として得られるテキストは、モデル設定で指定された日時と時刻の形式によって異なります。この形式から変換する場合、それらの設定に従って値の書式を設定する必要があります。時刻部分が先で、1つのスペースによって日付部分と区切る必要があります。
このコマンドでは、3000年およびそれ以後はサポートされないことに注意してください。
例
convert(42308, XL_DATETIME, MODEL_TIME) // Excelの日付を有効なモデル時間に変換する
days (num days)
与えられた日数内のモデル時間単位数を取得する
説明
与えられた日数に含まれるモデル時間単位数を返します。
例
days(3)
fpm (num feetperminute)
フィート/分に含まれるモデル長/時間単位数を取得する
説明
指定された数のフィート/分に含まれるモデル長/時間単位の数を返します。
例
fpm(9)
fps (num feetpersecond)
フィート/分に含まれるモデル長/時間単位数を取得する
説明
指定された数のフィート/秒に含まれるモデル長/時間単位の数を返します。
例
fps(9)
ft (num feet)
フィート数内のモデル長単位数を取得する
説明
指定された数のフィートに含まれるモデル長単位の数を返します。
例
ft(3)
hours (num hours)
時間数内のモデル時間単位数を取得する
説明
与えられた数の時間に含まれるモデル時間単位の数を返します。
例
hours(3)
in (num inches)
インチ数内のモデル長単位数を取得する
説明
指定された数のインチに含まれるモデル長単位の数を返します。
例
in(8)
minutes (num minutes)
分数内のモデル時間単位数を取得する
説明
指定された数の分に含まれるモデル時間単位の数を返します。
例
minutes(3);
180を返します。
180を返します。
mph (num milesperhour)
マイル/時間数に含まれるモデル長/時間単位数を取得する
説明
指定された数のマイル/時間に含まれるモデル長/時間単位の数を返します。
例
mph(9)
tonode (thing)
タイプをノードポインターとしてアサートする
説明
タイプをノードポインターとしてアサートします。C++でのみ実際の役割を果たします。
例
tonode(getnodenum(couplingnode))
couplingnodeの数値をtreenodeに変換する
couplingnodeの数値をtreenodeに変換する
tonum (thing)
タイプを数値としてアサートする
説明
タイプを数値としてアサートします。C++でのみ実際の役割を果たします。
例
return tonum(current);
現在のオブジェクトへのポインターを数値にキャストして返します。
現在のオブジェクトへのポインターを数値にキャストして返します。
toptr (thing)
説明
開発者向けです。タイプをポインターとしてアサートします。引数thingをタイプvoid*としてアサートします。C++でのみ実際の役割を果たしますが、flexscriptでも安全に使用できます。
例
toptr(so())
コンベヤ
conveyorgetmotor (obj conveyor)
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorgetmotor(conveyor);
conveyorinfo (obj conveyor, num info[, p1, p2, p3, p4, p5])
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorinfo(conveyor, CONV_INFO_ESTIMATE_CONVEY_TIME);
conveyorresumeitem (obj item[, num force])
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorresumeitem(item);
conveyorsenditem (obj item, obj dest)
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorsenditem(item, outobject(current, 1));
conveyorsetspeed (obj conveyor, num toSpeed)
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorsetspeed(conveyor, 1);
conveyorstopitem (obj item)
説明
廃止されました。Conveyorクラスを使用してください。
例
conveyorstopitem(item);
mergegetlanestate (obj mergeController, num laneNum)
説明
廃止されました。Conveyor.MergeControllerクラスを使用してください。
例
mergegetlanestate(current, 5)
mergegetnumlanes (obj mergeController)
説明
廃止されました。Conveyor.MergeControllerクラスを使用してください。
例
mergegetnumlanes(current)
mergeislaneclear (obj mergeController, num laneNum)
説明
廃止されました。Conveyor.MergeControllerクラスを使用してください。
例
mergeislaneclear(current, 5)
mergereleaselane (obj mergeController, num laneNum)
説明
廃止されました。Conveyor.MergeControllerクラスを使用してください。
例
mergereleaselane(current, 1)
廃止
コマンドのサポートが終了したか、別のコマンドが作成されました。これらのコマンドのドキュメントは更新されていないため、不正確な可能性があります。多くのコマンドは後方互換性のため依然として動作しますが、代替コマンドの使用をお勧めします。
acos (num ratio)
add (num value1, num value2)
廃止されました。+オペレーターを使用してください。
説明
このコマンドは廃止されました。代わりに+オペレーターを使用してください。
value1をvalue2に加算します。value1+value2の数値演算式の結果が返されます。
value1をvalue2に加算します。value1+value2の数値演算式の結果が返されます。
例
double sum = add(1,2);
addfullhistorymoverecord (num flowitemid, num time, obj origin, obj destination, num itemtype)
廃止
説明
このコマンドは廃止されました。移動テーブルに新しいエントリを追加します。このエントリは、全履歴が有効なときに記録されます。この新しいエントリは、flowitemidで識別されるフローアイテムが原点オブジェクトから目的地オブジェクトへ、指定した時間に移動したことを記録します。このエントリは、移動時点のフローアイテムのアイテムタイプが、3番目のパラメータとして渡されたitemtypeであることも記録します。ユーザーがこのコマンドを使用する必要があるのは非常に稀な状況のみです。
例
addfullhistorymoverecord(getnodenum(uniqueid(item)), time(), current, current.outObjects[1], item.type);
addfullhistorystaterecord (num time, num state, obj object)
廃止
説明
このコマンドは廃止されました。状態テーブルに新しいエントリを追加します。このエントリは、全履歴が有効なときに記録されます。この新しいエントリは、3番目のパラメータで渡された指定のオブジェクトが、最初のパラメータで入力された時間に、指定の状態に変化したことを記録します。このコマンドを呼び出す必要があるのは、setstate()以外のsoemコマンドでオブジェクトの状態が変化する場合のみです。
例
addfullhistorystaterecord(time(), STATE_IDLE, current);
addlabel (obj object, str labelname [, num/str value])
addtablecol (str/num/node table [, num column, num datatype])
addtablerow (str/num/node table [, num row, num datatype])
and (num/node condition1, num/node condition2)
廃止、&&オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに&&オペレーターを使用してください。
例
angle (num dx, num dy)
anode (thing)
廃止、tonode()を使用すること
説明
このコマンドは廃止されました。代わりにtonode()を使用してください。
タイプをノードポインターとしてアサートします。
タイプをノードポインターとしてアサートします。
例
anode(so())
anum (thing)
廃止、tonum()を使用すること
説明
このコマンドは廃止されました。代わりにtonum()を使用してください。
タイプを数値としてアサートします。
タイプを数値としてアサートします。
例
anum(so())
aptr (thing)
廃止、toptr()を使用すること
説明
このコマンドは廃止されました。代わりにtoptr()を使用してください。
タイプをポインターとしてアサートします。
タイプをポインターとしてアサートします。
例
aptr(so())
arraysize (var array)
asin (num ratio)
assertattribute (obj object, str attributename, num datatype)
assertlabel (obj object, str labelname, num datatype)
assertsubnode (node containernode, str name[, num datatype])
atan (num ratio)
att (obj object, num index)
廃止、getvarnode()を使用すること
説明
このコマンドは廃止されました。代わりにvar()、var_s()、getvarnode()を使用してください。
例
att(current,1)
att_s (obj object, str name)
廃止、getvarnode()を使用すること
説明
このコマンドは廃止されました。代わりにgetvarnode()を使用してください。
オブジェクトの属性ノードを名前で取得します。属性ノードは、オブジェクトの構造の「変数」ノード内に存在するものです。この関数は、オブジェクトの変数ノード内にある、nameで指定された名前のノードへのポインターを返します。このコマンドはvar_sに置き換えられました。
オブジェクトの属性ノードを名前で取得します。属性ノードは、オブジェクトの構造の「変数」ノード内に存在するものです。この関数は、オブジェクトの変数ノード内にある、nameで指定された名前のノードへのポインターを返します。このコマンドはvar_sに置き換えられました。
例
att_s(current,"myatt")
aviadd (node viewnode)
説明
このコマンドは廃止されました。代わりに動画レコーダーを使用してください。
例
avifinish (node viewnode)
説明
このコマンドは廃止されました。代わりに動画レコーダーを使用してください。
例
avistart (str filename, node viewnode, num fps)
説明
このコマンドは廃止されました。代わりに動画レコーダーを使用してください。
例
bcgetitemkinematics (obj basicconveyor, obj item, num kinematictype {0 - メインキネマティクス、1 - 時間に依存、2 - 搬送に依存})
廃止、レガシーコンベヤのサポートは終了
説明
廃止されました。レガシーコンベヤのサポートは終了しました。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcgetitemkinematicsコマンドは、BasicConveyorのフローアイテム移動に関連付けられている3つのキネマティクスのいずれかへの参照を取得するため使用されます。
0 = メインコンベヤ状態キネマティクス。これからキネマティクス情報を取得できますが、キネマティクスに追加や初期化の変更を加えることはできません。
1 = ユーザー定義可能なキネマティクスで、シミュレーション時間に依存します。
2 = ユーザー定義可能なキネマティクスで、コンベヤ上のフローアイテムの搬送位置に依存します。
2つのユーザー定義可能なキネマティクスは、ユーザーがコンベヤの長さに応じた移動に加え、カスタマイズされたキネマティクス動作をセットアップするため使用できます。bcgetitemkinematicsを使用して目的のキネマティクスノードへの参照を取得してから、標準のinitkinematics()およびaddkinematic()コマンドを通常に使用します。代替のinitkinematicsパラメータリストとして、initkinematics(node, x, y, z, rx, ry, rz, managerots, localcoords)を使用する必要があります。また、タイプ2の搬送依存のキネマティクスノードにキネマティクスを追加する場合、そのキネマティクス用の時間単位はどれも、実際のシミュレーションの時間単位には適用されないことに注意してください。代わりに、それらの時間単位は「搬送単位」と解釈されます。たとえば、速度5は時間単位当たり5単位とは解釈されず、搬送単位ごとに5単位と解釈されます。加速は時間あたりの距離の二乗ではなく、搬送単位ごとの距離の二乗です。開始時間はキネマティクスを開始する時間ではなく、コンベヤに沿った位置がキネマティクスを開始する時間です。例として、「start time」 5および「max speed」 0.5を使用して、搬送依存のキネマティクスノードに、y方向へ1単位移動するキネマティクスを追加したとします。搬送依存のキネマティクスでは、アイテムがコンベヤに沿って5単位に到達してから、y方向に移動を開始すると解釈されます。また、コンベヤの長さに沿って移動するすべての単位について、y方向に0.5単位移動します(搬送単位ごとに0.5 y単位)。このため、コンベヤに沿って7単位移動すると、yキネマティクスは終了します。アイテムが累積によって中間、たとえば搬送位置6でブロックされた場合、yキネマティクスも停止して、アイテムがコンベヤに沿った移動を再開するまではキネマティクスも再開されません。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcgetitemkinematicsコマンドは、BasicConveyorのフローアイテム移動に関連付けられている3つのキネマティクスのいずれかへの参照を取得するため使用されます。
0 = メインコンベヤ状態キネマティクス。これからキネマティクス情報を取得できますが、キネマティクスに追加や初期化の変更を加えることはできません。
1 = ユーザー定義可能なキネマティクスで、シミュレーション時間に依存します。
2 = ユーザー定義可能なキネマティクスで、コンベヤ上のフローアイテムの搬送位置に依存します。
2つのユーザー定義可能なキネマティクスは、ユーザーがコンベヤの長さに応じた移動に加え、カスタマイズされたキネマティクス動作をセットアップするため使用できます。bcgetitemkinematicsを使用して目的のキネマティクスノードへの参照を取得してから、標準のinitkinematics()およびaddkinematic()コマンドを通常に使用します。代替のinitkinematicsパラメータリストとして、initkinematics(node, x, y, z, rx, ry, rz, managerots, localcoords)を使用する必要があります。また、タイプ2の搬送依存のキネマティクスノードにキネマティクスを追加する場合、そのキネマティクス用の時間単位はどれも、実際のシミュレーションの時間単位には適用されないことに注意してください。代わりに、それらの時間単位は「搬送単位」と解釈されます。たとえば、速度5は時間単位当たり5単位とは解釈されず、搬送単位ごとに5単位と解釈されます。加速は時間あたりの距離の二乗ではなく、搬送単位ごとの距離の二乗です。開始時間はキネマティクスを開始する時間ではなく、コンベヤに沿った位置がキネマティクスを開始する時間です。例として、「start time」 5および「max speed」 0.5を使用して、搬送依存のキネマティクスノードに、y方向へ1単位移動するキネマティクスを追加したとします。搬送依存のキネマティクスでは、アイテムがコンベヤに沿って5単位に到達してから、y方向に移動を開始すると解釈されます。また、コンベヤの長さに沿って移動するすべての単位について、y方向に0.5単位移動します(搬送単位ごとに0.5 y単位)。このため、コンベヤに沿って7単位移動すると、yキネマティクスは終了します。アイテムが累積によって中間、たとえば搬送位置6でブロックされた場合、yキネマティクスも停止して、アイテムがコンベヤに沿った移動を再開するまではキネマティクスも再開されません。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
例
treenode kin = bcgetitemkinematics(current, item, 2);
treenode kin2 = bcgetitemkinematics(current, item, 1);
initkinematics(kin, 0,0,0, 0,0,0, 0,0);
addkinematic(kin, 0,1,1,0.5,1,1,0,0, 5, KINEMATIC_TRAVEL);
initkinematics(kin2, 0,0,0, 0,0,0, 0,0);
addkinematic(kin2, 0,0,720,360,0,0,0,0, time()+5.0, KINEMATIC_ROTATE);
treenode kin2 = bcgetitemkinematics(current, item, 1);
initkinematics(kin, 0,0,0, 0,0,0, 0,0);
addkinematic(kin, 0,1,1,0.5,1,1,0,0, 5, KINEMATIC_TRAVEL);
initkinematics(kin2, 0,0,0, 0,0,0, 0,0);
addkinematic(kin2, 0,0,720,360,0,0,0,0, time()+5.0, KINEMATIC_ROTATE);
bcgetitemposition (obj basicconveyor, obj item)
廃止、レガシーコンベヤのサポートは終了
説明
廃止されました。レガシーコンベヤのサポートは終了しました。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcgetitempositionコマンドは、BasicConveyorオブジェクト上のアイテムの現在位置を返します。この位置は、コンベヤの長さに沿って、コンベヤの頭部から、フローアイテムでコンベヤの頭部から最も離れたエッジまで測定されます。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcgetitempositionコマンドは、BasicConveyorオブジェクト上のアイテムの現在位置を返します。この位置は、コンベヤの長さに沿って、コンベヤの頭部から、フローアイテムでコンベヤの頭部から最も離れたエッジまで測定されます。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
例
bcgetitemposition(current,current.first);
bcsetdirection (obj basicconveyor, num direction)
廃止、レガシーコンベヤのサポートは終了
説明
廃止されました。レガシーコンベヤのサポートは終了しました。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcsetdirectionコマンドは、コンベヤ上のすべてのフローアイテムを停止し、移動方向を1=順方向および0=逆方向に設定します。すべてのフローアイテムは、再度移動を開始する前にbcsetitemconveystate()コマンドで搬送状態をリセットする必要があります。次の例は、コンベヤを停止してから、すべてのフローアイテムを逆方向に速度1まで加速する方法を示しています。すべての追加アイテムキネマティクスは、方向の変更後もアクティブのままです。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
bcsetdirectionコマンドは、コンベヤ上のすべてのフローアイテムを停止し、移動方向を1=順方向および0=逆方向に設定します。すべてのフローアイテムは、再度移動を開始する前にbcsetitemconveystate()コマンドで搬送状態をリセットする必要があります。次の例は、コンベヤを停止してから、すべてのフローアイテムを逆方向に速度1まで加速する方法を示しています。すべての追加アイテムキネマティクスは、方向の変更後もアクティブのままです。
BasicConveyorオブジェクトの一般的な説明については、bcsetitemconveystateコマンドのドキュメントを参照してください。
例
bcsetdirection(so(),0);
for(int i = 1; i <= so().subnodes.length; i++)
{
treenode item = so().subnodes[i];
bcsetitemconveystate(so(), item, bcgetitemposition(so(), item), 0, 1, 0.2);
}
for(int i = 1; i <= so().subnodes.length; i++)
{
treenode item = so().subnodes[i];
bcsetitemconveystate(so(), item, bcgetitemposition(so(), item), 0, 1, 0.2);
}
bcsetitemconveystate (obj basicconveyor, obj item, num startpoint, num startspeed, num targetspeed, num accdec)
廃止、レガシーコンベヤのサポートは終了
説明
廃止されました。レガシーコンベヤのサポートは終了しました。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
BasicConveyorオブジェクトを使用すると、フローアイテムをどの時点、どの位置でもコンベヤの中に、またはコンベヤから外に移動できます。BasicConveyorの各フローアイテムに独自のキネマティクスプロファイルを割り当ておよび再割り当てし、フローアイテムがコンベヤに沿ってどのように移動するかを定義できます。1つのフローアイテムが、コンベヤ上で停止または低速で移動している他のフローアイテムに追い付くと、そのフローアイテムの速度に合わせてただちに減速されます。フローアイテムはコンベヤに沿ってどちらの方向にも移動する可能性がありますが、特定の時点で見ると、すべてのフローアイテムが同じ方向に移動します。コンベヤの移動方向はbcsetdirection()コマンドで設定されます。フローアイテムがコンベヤの中に、またはコンベヤから外に移動するとき、コンベヤ上の他のフローアイテムはコンベヤ上で利用可能な空間が増加または減少したことを認識し、自然に集積を行います。フローアイテムがコンベヤに進入した後で、receiveitem()コマンドで間接的に、またはmoveobject()コマンドで直接的に、フローアイテムの初期キネマティクスプロファイルを定義する必要があります。このプロファイルはフローアイテムの「搬送状態」と呼ばれ、bcsetitemconveystate()コマンドで設定されます。フローアイテムの搬送状態は、必要に応じて何回でも設定できます。フローアイテムの搬送状態を定義するため使用されるパラメータの定義は次のとおりです。
basicconveyor = コンベヤへの参照。
item = フローアイテムへの参照。
startpoint = フローアイテムの開始位置。コンベヤの先頭から、コンベヤの長さ方向に沿って、コンベヤの頭から最も離れたフローアイテムのエッジまで測定されます(コンベヤの方向が順方向なら前縁、逆方向なら後縁)。
startspeed = フローアイテムの移動開始時の速度。
targetspeed = フローアイテムが到達を試みる目標速度。targetspeedがstartspeedよりも大きい場合、フローアイテムは目標速度まで加速します。そうでない場合、目標速度まで減速します。startspeedとtargetspeedが両方とも0に設定されている場合、フローアイテムはstartpointのまま移動しません。
accdec = 時間の経過とともに目標速度に到達するため使用される、加速度または減速度。値が0なら、無限大の加速度/減速度を意味します。言い換えれば、フローアイテムは一瞬でtargetspeedに達します。
フローアイテムは、コンベヤの終端に到達する、別のフローアイテムに衝突する、または搬送状態が再度変更されるまでコンベヤに沿って移動を続けるため、目的地や終端速度は必要ありません。BasicConveyorでは、長さ方向に沿って複数の「決定点」を定義できます。これらのトリガーポイントは、フローアイテムの搬送状態を更新するため便利な場所です。フローアイテムには、bcsetitemconveystate()コマンドで割り当てられたメイン搬送状態キネマティクスに加え、2つの別のキネマティクス構造が関連付けられており、コンベヤに沿った移動の動作だけでなく、カスタムのキネマティクス動作(平行移動または回転)も適用できます。キネマティクス構造の1つはシミュレーションの時間単位に基づいており、もう1つはコンベヤの長さ方向に沿った距離単位に基づいています。これらのキネマティクス構造にアクセスするには、bcgetitemkinematics()コマンドを使用してからinitkinematics()およびaddkinematic()コマンドを使用して、必要なカスタムキネマティクス動作を作成します。詳細については、bcgetitemkinematics()コマンドのドキュメントを参照してください。
このコマンドは、BasicConveyorオブジェクトと組み合わせて使用されます。
BasicConveyorオブジェクトを使用すると、フローアイテムをどの時点、どの位置でもコンベヤの中に、またはコンベヤから外に移動できます。BasicConveyorの各フローアイテムに独自のキネマティクスプロファイルを割り当ておよび再割り当てし、フローアイテムがコンベヤに沿ってどのように移動するかを定義できます。1つのフローアイテムが、コンベヤ上で停止または低速で移動している他のフローアイテムに追い付くと、そのフローアイテムの速度に合わせてただちに減速されます。フローアイテムはコンベヤに沿ってどちらの方向にも移動する可能性がありますが、特定の時点で見ると、すべてのフローアイテムが同じ方向に移動します。コンベヤの移動方向はbcsetdirection()コマンドで設定されます。フローアイテムがコンベヤの中に、またはコンベヤから外に移動するとき、コンベヤ上の他のフローアイテムはコンベヤ上で利用可能な空間が増加または減少したことを認識し、自然に集積を行います。フローアイテムがコンベヤに進入した後で、receiveitem()コマンドで間接的に、またはmoveobject()コマンドで直接的に、フローアイテムの初期キネマティクスプロファイルを定義する必要があります。このプロファイルはフローアイテムの「搬送状態」と呼ばれ、bcsetitemconveystate()コマンドで設定されます。フローアイテムの搬送状態は、必要に応じて何回でも設定できます。フローアイテムの搬送状態を定義するため使用されるパラメータの定義は次のとおりです。
basicconveyor = コンベヤへの参照。
item = フローアイテムへの参照。
startpoint = フローアイテムの開始位置。コンベヤの先頭から、コンベヤの長さ方向に沿って、コンベヤの頭から最も離れたフローアイテムのエッジまで測定されます(コンベヤの方向が順方向なら前縁、逆方向なら後縁)。
startspeed = フローアイテムの移動開始時の速度。
targetspeed = フローアイテムが到達を試みる目標速度。targetspeedがstartspeedよりも大きい場合、フローアイテムは目標速度まで加速します。そうでない場合、目標速度まで減速します。startspeedとtargetspeedが両方とも0に設定されている場合、フローアイテムはstartpointのまま移動しません。
accdec = 時間の経過とともに目標速度に到達するため使用される、加速度または減速度。値が0なら、無限大の加速度/減速度を意味します。言い換えれば、フローアイテムは一瞬でtargetspeedに達します。
フローアイテムは、コンベヤの終端に到達する、別のフローアイテムに衝突する、または搬送状態が再度変更されるまでコンベヤに沿って移動を続けるため、目的地や終端速度は必要ありません。BasicConveyorでは、長さ方向に沿って複数の「決定点」を定義できます。これらのトリガーポイントは、フローアイテムの搬送状態を更新するため便利な場所です。フローアイテムには、bcsetitemconveystate()コマンドで割り当てられたメイン搬送状態キネマティクスに加え、2つの別のキネマティクス構造が関連付けられており、コンベヤに沿った移動の動作だけでなく、カスタムのキネマティクス動作(平行移動または回転)も適用できます。キネマティクス構造の1つはシミュレーションの時間単位に基づいており、もう1つはコンベヤの長さ方向に沿った距離単位に基づいています。これらのキネマティクス構造にアクセスするには、bcgetitemkinematics()コマンドを使用してからinitkinematics()およびaddkinematic()コマンドを使用して、必要なカスタムキネマティクス動作を作成します。詳細については、bcgetitemkinematics()コマンドのドキュメントを参照してください。
例
bcsetitemconveystate(current, item, position, 0, 60, 0);
bitwiseand (num a, num b)
廃止、&オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに&オペレーターを使用してください。
2つの32ビット整数値のビット単位AND演算の結果を返します。
2つの32ビット整数値のビット単位AND演算の結果を返します。
例
int bwa = bitwiseand(0x460, 0x040);
この例は、bwaを値0x020に設定します。
この例は、bwaを値0x020に設定します。
bitwisenot (num a)
廃止、~オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに~オペレーターを使用してください。
32ビット整数値のビット単位NOTの結果を返します。
32ビット整数値のビット単位NOTの結果を返します。
例
int bwn = bitwisenot(0x0);
この例は、bwnを値0xffffffffに設定します。
この例は、bwnを値0xffffffffに設定します。
bitwiseor (num a, num b)
廃止、|オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに|オペレーターを使用してください。
32ビット整数値のビット単位ORの結果を返します。
32ビット整数値のビット単位ORの結果を返します。
例
int bwa = bitwiseand(0x15, 0x01);
この例は、bwoを値0x15に設定します。
この例は、bwoを値0x15に設定します。
bitwisexor (num a, num b)
廃止、^オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに^オペレーターを使用してください。
32ビット整数値のビット単位XORの結果を返します。
32ビット整数値のビット単位XORの結果を返します。
例
int bwxo = bitwisexor(0x15, 0x01);
この例は、bwxo を値0x14に設定します。
この例は、bwxo を値0x14に設定します。
ceil (num num)
cell (node table, num col, num row)
cellrc (obj object, num row, num col)
cellrowcolumn (node table, num row, num col)
廃止、Tableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスを使用してください。
例
centerobject (obj object, num centerportnum)
廃止、Object.centerObjects[]を使用すること
説明
例
changeconveyorspeed (obj conveyor, num newspeed )
廃止、conveyor.targetSpeedを使用すること
説明
例
changeconveyorspeed(current, 4);
この例は、コンベヤの速度を4に変更します。
この例は、コンベヤの速度を4に変更します。
clearconsole ()
出力コンソールをクリアする
説明
このコマンドは、出力コンソールが開いているなら、クリアします。出力コンソールは、pt()、pf()、pr()コマンドの出力が表示される場所です。
例
if (v_printerror == 1)
{
clearconsole();
pt("An Error occurred");
}
出力コンソールをクリアし、変数printerrorが1の場合は簡単なエラーメッセージを表示します。
{
clearconsole();
pt("An Error occurred");
}
出力コンソールをクリアし、変数printerrorが1の場合は簡単なエラーメッセージを表示します。
clearcontents (node thenode)
clearfullhistory (int resetuniqueid)
廃止
説明
このコマンドは廃止されました。全履歴システムにより収集されたすべてのデータを削除します。resetuniqueidが1なら、このコマンドが呼び出された後で作成されるフローアイテムの固有IDは、また1から始まります。このパラメータは通常は0で、以前のフローアイテムと新しいフローアイテムの混同がないよう、番号付けがリセットされずに続けられます。
例
clearfullhistory(0);
clearglobaltable (str/node/num table)
廃止、Tableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスを使用してください。
例
closeinput (obj object)
廃止、Object.input.close()を使用すること
説明
このコマンドは廃止されました。代わりにUse Object.input.close()を使用してください。
このコマンドは、オブジェクトの入力をブロックします。エントリをブロックするには、入力ポート自体、または一般的な入力のみを閉じる必要があります。ポート接続がビューウィンドウに十分なサイズで表示されているとき、オブジェクトの入力ポート(正方形)すべてにわたって小さな赤色のバーが描画され、入力ポートがブロックされていることを示します。個別のポートを開くことはでき、開いているポートは緑色で表示されますが、赤いバーのためにオブジェクトへの進入はブロックされます。このコマンドをstopinput()と比較してください。
このコマンドは、オブジェクトの入力をブロックします。エントリをブロックするには、入力ポート自体、または一般的な入力のみを閉じる必要があります。ポート接続がビューウィンドウに十分なサイズで表示されているとき、オブジェクトの入力ポート(正方形)すべてにわたって小さな赤色のバーが描画され、入力ポートがブロックされていることを示します。個別のポートを開くことはでき、開いているポートは緑色で表示されますが、赤いバーのためにオブジェクトへの進入はブロックされます。このコマンドをstopinput()と比較してください。
例
if (current.subnodes.length == getvarnum(current,"maxcontent")
closeinput(current);
current内のオブジェクトが多すぎる場合、currentの入力ポートをブロックします。
closeinput(current);
current内のオブジェクトが多すぎる場合、currentの入力ポートをブロックします。
closeoutput (obj object)
廃止、Object.output.close()を使用すること
説明
このコマンドは廃止されました。代わりにObject.output.close()を使用してください。
このコマンドは、オブジェクトの出力をブロックします。出口をブロックするには、出力ポート自体、または一般的な出力のみを閉じる必要があります。ポート接続がビューウィンドウに十分なサイズで表示されているとき、オブジェクトの出力ポート(正方形)すべてにわたって小さな赤色のバーが描画され、出力ポートがブロックされていることを示します。個別のポートを開くことはでき、開いているポートは緑色で表示されますが、赤いバーのためにオブジェクトからの出口はブロックされます。このコマンドをstopoutput()と比較してください。
このコマンドは、オブジェクトの出力をブロックします。出口をブロックするには、出力ポート自体、または一般的な出力のみを閉じる必要があります。ポート接続がビューウィンドウに十分なサイズで表示されているとき、オブジェクトの出力ポート(正方形)すべてにわたって小さな赤色のバーが描画され、出力ポートがブロックされていることを示します。個別のポートを開くことはでき、開いているポートは緑色で表示されますが、赤いバーのためにオブジェクトからの出口はブロックされます。このコマンドをstopoutput()と比較してください。
例
if (current.subnodes.length == current.mincontent)
closeoutput(current);
current内のオブジェクトが少なすぎる場合、currentの出力ポートをブロックします。
closeoutput(current);
current内のオブジェクトが少なすぎる場合、currentの出力ポートをブロックします。
coloraqua (obj object)
colorarray (obj object, num colornumber)
colorblack (obj object)
colorblue (obj object)
colorbrown (obj object)
colorgray (obj object)
colorgreen (obj object)
colorlightblue (obj object)
colorlime (obj object)
colororange (obj object)
colorpink (obj object)
colorpurple (obj object)
colorrandom (obj object)
colorred (obj object)
colorrgb (obj object, num red, num green, num blue)
colorsilver (obj object)
colorteal (obj object)
colorwhite (obj object)
coloryellow (obj object)
comparetext (str text1, str text2[, int ignorecase])
廃止、==オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに==オペレーターを使用してください。myStr == "Hello"
で文字列が等しいかどうかテストできます。
で文字列が等しいかどうかテストできます。
例
concat (str text1, str text2 [, str text3, ...])
廃止、+オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに+オペレーターを使用してください。"a" + "b" + "c"
文字列を互いに連結します。
文字列を互いに連結します。
例
connect (obj object1, num port1, obj object2, num port2)
廃止、contextdragconnection()を使用すること
説明
このコマンドは廃止されました。代わりにcontextdragconnection()を使用してください。
2つのオブジェクトのポートを接続します。2つのオブジェクトを接続するため、該当のオブジェクトにポートが存在するかどうかチェックしてから、接続が行われます。最初のオブジェクトの出力ポートは、2番目のオブジェクトの入力に接続されます。ポートが存在しない、または既に接続済みのとき、このコマンドは中断されます。2つのオブジェクトを、ポートを追加して自動的に接続するには、objectconnect()コマンドを参照してください。
2つのオブジェクトのポートを接続します。2つのオブジェクトを接続するため、該当のオブジェクトにポートが存在するかどうかチェックしてから、接続が行われます。最初のオブジェクトの出力ポートは、2番目のオブジェクトの入力に接続されます。ポートが存在しない、または既に接続済みのとき、このコマンドは中断されます。2つのオブジェクトを、ポートを追加して自動的に接続するには、objectconnect()コマンドを参照してください。
例
connect(model().subnodes[2],1,model().subnodes[3],2)
containerentry (obj container, obj item)
廃止、追跡変数または処理フローを使用すること
説明
このコマンドは廃止されました。カスタム統計を追跡するには、追跡変数、処理フロー、または両方を使用してください。
例
containerexit (obj container, obj item)
廃止、追跡変数または処理フローを使用すること
説明
このコマンドは廃止されました。カスタム統計を追跡するには、追跡変数、処理フロー、または両方を使用してください。
例
contentobj (obj container)
cos (num angle)
count ()
説明
repeat()、findmatch()、findmin()、findmax()などのコマンドに使用される反復子の値。countの値は、現在どの反復が実行されているかによって異なります。
例
findmax(Table("MyTable").numRows, Table("MyTable")[count][5])
テーブルMyTableのすべての行について、列5の最大値を返します。
テーブルMyTableのすべての行について、列5の最大値を返します。
cppgettoken (obj textblock, num tokenindex)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
cppsettoken (obj textblock, num tokenindex, str insertiontext)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
createdelaytask (obj dispatcher, num delaytime, num state, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、dispatcherにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、現在のタスクはdelaytime秒だけ一時停止されます。遅延時間の間は、stateで指定される状態に維持されます。タスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、dispatcherにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、現在のタスクはdelaytime秒だけ一時停止されます。遅延時間の間は、stateで指定される状態に維持されます。タスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createdelaytask(current.centerObjects[1], 25, SCHEDULED_DOWN, 1, PREEMPT_NOT);
createglobaltasksequence (str name, obj dispatcher [, obj dp1, obj dp2, obj dp3, obj dp4, obj dp5])
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
与えられた動的パラメータ1~5を使用して名前付きグローバルタスクシーケンスのインスタンスを作成し、指定のディスパッチャーに送付します。作成されたグローバルタスクシーケンスへの参照が返されます。このコマンドはタスクシーケンスを送付しないことに注意してください。送付はdispatchtasksequence()を使用して行う必要があります。
与えられた動的パラメータ1~5を使用して名前付きグローバルタスクシーケンスのインスタンスを作成し、指定のディスパッチャーに送付します。作成されたグローバルタスクシーケンスへの参照が返されます。このコマンドはタスクシーケンスを送付しないことに注意してください。送付はdispatchtasksequence()を使用して行う必要があります。
例
treenode ts = createglobaltasksequence("GlobalTS", current.centerObjects[1])
dispatchtasksequence(ts)
dispatchtasksequence(ts)
createloadtask (obj taskexecuter, obj destination, obj flowitem, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、フローアイテムがロードされます。オフジェクトは、フローアイテムをロードする前に、フローアイテムへ移動しません。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、フローアイテムがロードされます。オフジェクトは、フローアイテムをロードする前に、フローアイテムへ移動しません。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createloadtask(current.centerObjects[1],current.centerObjects[2],item, 1, PREEMPT_NOT);
createsendmessagetask (obj taskexecuter, obj receiver, num priority, num preempting , num param1, num param2, num param3)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、dispatcherにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、receiverで指定されたオブジェクトにメッセージが送信されます。受信側オブジェクトのOnMessageトリガーは、メッセージの送信時に実行されます。param1、param2、param3で渡される値は、param()コマンドを使用してトリガー関数で使用可能です。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、dispatcherにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、receiverで指定されたオブジェクトにメッセージが送信されます。受信側オブジェクトのOnMessageトリガーは、メッセージの送信時に実行されます。param1、param2、param3で渡される値は、param()コマンドを使用してトリガー関数で使用可能です。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです:
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createsendmessagetask(current, current.centerObjects[1],1,PREEMPT_NOT,5, 6, 7);
createstandardtask (obj taskexecuter, obj origin, obj destination, obj flowitem, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これによりオブジェクトは原点に移動し、フローアイテムをロードして、目的地に移動してから、フローアイテムをアンロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これによりオブジェクトは原点に移動し、フローアイテムをロードして、目的地に移動してから、フローアイテムをアンロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createstandardtaskcurrent.centerObjects[1],current.centerObjects[2],current.centerObjects[3],item, 1, PREEMPT_NOT);
createtravelloadtask (obj taskexecuter, obj destination, obj flowitem, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動してフローアイテムをロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動してフローアイテムをロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createtravelloadtask(current.centerObjects[1],current.centerObjects[2],item, 1, PREEMPT_NOT);
createtraveltask (obj taskexecuter, obj destination, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動します。オブジェクトは、前端が目的地に到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動します。オブジェクトは、前端が目的地に到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createtraveltask( current.centerObjects[1], current.centerObjects[2], 1, PREEMPT_NOT);
createtraveltolocandwaittask (obj taskexecuter, num relativeloc, num x, num y, num z, num endspeed, num state, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはxlox、y、zにより指定されたポイントに移動します。オブジェクトがそのポイントに到達すると、stateで指定された状態のまま、endwaittask()がそのオブジェクトに対して発行されるまで待機します。有効な状態のリストについては、setstate()を参照してください。relativelocが1なら、指定されたポイントはディスパッチャーの原点に対する相対位置です。relativelocが0なら、指定されたポイントは
モデルの中でディスパッチャーの移動先となる正確なポイントです。オブジェクトは、前端が指定されたポイントに到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはxlox、y、zにより指定されたポイントに移動します。オブジェクトがそのポイントに到達すると、stateで指定された状態のまま、endwaittask()がそのオブジェクトに対して発行されるまで待機します。有効な状態のリストについては、setstate()を参照してください。relativelocが1なら、指定されたポイントはディスパッチャーの原点に対する相対位置です。relativelocが0なら、指定されたポイントは
モデルの中でディスパッチャーの移動先となる正確なポイントです。オブジェクトは、前端が指定されたポイントに到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createtraveltolocandwaittask(current.centerObjects[1], 1, 5.15, 2.5, 0, 0, STATE_IDLE, 1, PREEMPT_NOT);
createtraveltoloctask (obj dispatcher, num relativeloc, num x, num y, num z, num endspeed, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはxlox、y、zにより指定されたポイントに移動します。relativelocが1なら、指定されたポイントはディスパッチャーの原点に対する相対位置です。relativelocが0なら、指定されたポイントはモデルの中でディスパッチャーの移動先となる正確なポイントです。オブジェクトは、前端が指定されたポイントに到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはxlox、y、zにより指定されたポイントに移動します。relativelocが1なら、指定されたポイントはディスパッチャーの原点に対する相対位置です。relativelocが0なら、指定されたポイントはモデルの中でディスパッチャーの移動先となる正確なポイントです。オブジェクトは、前端が指定されたポイントに到達するまで移動します。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createtraveltoloctask(current.centerObjects[1], 1, 5.15, 2.5, 0, 0, 1, PREEMPT_NOT);
createtravelunloadtask (obj taskexecuter, obj destination, obj flowitem, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動してフローアイテムをアンロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトは目的地に移動してフローアイテムをアンロードします。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createtravelunloadtask(current.centerObjects[1],current.centerObjects[2],item, 1, PREEMPT_NOT);
createunloadtask (obj dispatcher, obj destination, obj flowitem, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、destinationで指定されたオブジェクトにフローアイテムがアンロードされます。オブジェクトはアンロードの前に、指定場所に移動しません。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーにより指定されるオブジェクトのタスクシーケンスを作成します。これにより、destinationで指定されたオブジェクトにフローアイテムがアンロードされます。オブジェクトはアンロードの前に、指定場所に移動しません。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createunloadtask(current.centerObjects[1],current.centerObjects[2],item, 1, PREEMPT_NOT);
createwaittask (obj taskexecuter, num state, num priority, num preempting)
廃止、代わりに処理フローを使用すること
説明
このコマンドは廃止されました。代わりに処理フローを使用してください。
このコマンドは、ディスパッチャーとして指定されたオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはリリースされるまで、与えられる新しいタスクシーケンスを実行しません。オブジェクトはendwaittask()コマンドでリリースできます。オブジェクトは待機中、stateで指定される状態に維持されます。可能な状態のリストについては、setstate()コマンドを参照してください。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
このコマンドは、ディスパッチャーとして指定されたオブジェクトのタスクシーケンスを作成します。これにより、オブジェクトはリリースされるまで、与えられる新しいタスクシーケンスを実行しません。オブジェクトはendwaittask()コマンドでリリースできます。オブジェクトは待機中、stateで指定される状態に維持されます。可能な状態のリストについては、setstate()コマンドを参照してください。このタスクシーケンスの優先度はpriorityで、プリエンプト値はpreemptingで与えられます。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createwaittask(current.centerObjects[1], STATE_IDLE, 1, PREEMPT_NOT);
current <括弧なし>
説明
このコマンドは廃止されました。このコマンドは、今後setcurrentコマンドとともに特殊コマンドとして使用してはいけません。代わりに、treenode変数タイプをcurrentとして宣言し、コード内で他の変数タイプと同様にcurrentを使用してください。
例
treenode current = model().subnodes[3];
pt(current.name);
モデル内で3にランクされるオブジェクトをcurrentに設定し、出力コンソールにその名前を表示します。
pt(current.name);
モデル内で3にランクされるオブジェクトをcurrentに設定し、出力コンソールにその名前を表示します。
dbwritechanges ()
廃止
説明
このコマンドは廃止されました。
変更内容でデータベースを更新してください。
変更内容でデータベースを更新してください。
例
dbwritechanges()
defaultdragconnection (obj fromobject, obj toobject, char characterpressed)
廃止、contextdragconnection()を使用すること
説明
このコマンドは廃止されました。代わりにcontextdragconnection()を使用してください。
指定されたcharacterpressedに応じて、fromobjectとtoobjectとの間のポートを接続または接続解除します。このコマンドは、オブジェクトのポートを接続/切断するため使用されるキーボートおよびマウスの操作を模倣します。たとえば、「A」はキーボードの「A」を押し下げたまま、fromobjectをクリックしてtoobjectにドラッグする操作に相当します。「A」および「Q」なら、出力ポートを入力ポートに接続および接続解除します。「S」および「W」なら、セントラルポートを接続および接続解除します。C++でのみ使用でき、flexscriptでは使用できません。
指定されたcharacterpressedに応じて、fromobjectとtoobjectとの間のポートを接続または接続解除します。このコマンドは、オブジェクトのポートを接続/切断するため使用されるキーボートおよびマウスの操作を模倣します。たとえば、「A」はキーボードの「A」を押し下げたまま、fromobjectをクリックしてtoobjectにドラッグする操作に相当します。「A」および「Q」なら、出力ポートを入力ポートに接続および接続解除します。「S」および「W」なら、セントラルポートを接続および接続解除します。C++でのみ使用でき、flexscriptでは使用できません。
例
defaultdragconnection(model().subnodes[count], model().subnodes[2], 'A')
degreestoradians (num degrees)
deletetablecol (str/num/node table, num column)
deletetablerow (str/num/node table, num row)
dellabel (obj object, str/num label)
destroyobject (node thenode)
diffsign (num value1, num value2)
div (num value1, num value2)
廃止、/オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに/オペレーターを使用してください。
value1をvalue2で除算します。value2が0のとき計算は中断され、0が返されます。
value1をvalue2で除算します。value2が0のとき計算は中断され、0が返されます。
例
div(10,2)
divide (num value1, num value2)
廃止、/オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに/オペレーターを使用してください。
これはdiv()のエイリアスです。
これはdiv()のエイリアスです。
例
divide(10,2)
dumpquery (node dumpNode[, num asTable])
enablefullhistory (num on/off)
廃止
説明
このコマンドは廃止されました。全履歴収集をオン/オフします。渡されたパラメータが1なら、全履歴がオンになります。0ならオフになります。このコマンドは直接呼び出しません。代わりに、[全履歴を有効にする]メニューオプションを使用して全履歴をオン/オフしてください。
例
enablefullhistory(1); // 全履歴収集をオンにする
endwaittask (obj taskexecuter)
廃止、処理フローまたはfreeoperators()を使用すること
説明
このコマンドは廃止されました。代わりに、処理フローまたはfreeoperators()コマンドを使用してください。
このコマンドは、ディスパッチャーとして指定されたオブジェクトを、createwaittask()により発行された待機タスクからリリースします。オブジェクトがリリースされると以前の状態に戻り、タスクシーケンスキューに存在するタスクシーケンスの実行を開始します。
このコマンドは、ディスパッチャーとして指定されたオブジェクトを、createwaittask()により発行された待機タスクからリリースします。オブジェクトがリリースされると以前の状態に戻り、タスクシーケンスキューに存在するタスクシーケンスの実行を開始します。
例
endwaittask(current.centerObjects[1]);
eq (num/node value1, num/node value2)
廃止、==オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに==オペレーターを使用してください。
例
excelexportnode (node table, num startrow, num startcol, num numrows, num numcols [, num rowchar, num colchar])
廃止、excelexporttable()を使用すること
説明
このコマンドは廃止されました。代わりにexcelexporttable()を使用してください。
例
excelexportnode(reftable("Table1"),1,1,5,3);
excelimportnode (obj node, num startrow, num startcol, num numrows, num numcols [, num rowchar, num colchar])
廃止、excelimporttable()を使用すること
説明
このコマンドは廃止されました。代わりにexcelimporttable()を使用してください。
例
excelimportnode(so(),1,1,5,3);
excelmacro (str macro)
廃止
説明
このコマンドは廃止されました。このコマンドは、ユーザーがExcel 4.0のマクロコマンドをExcelに送信するためのものです。この言語はMicrosoftでのサポートが終了しており、Excelの将来のバージョンでは削除される可能性があります。
例
excelmacro("select(\"r1c1:r5c5\")");
ワークブックの行1、列1から行5、列5までのセクションを選択します。
ワークブックの行1、列1から行5、列5までのセクションを選択します。
excelrangeread (str rangename[treenode target], num row, num col[, num numRows, num numCols, num flags])
Excelの範囲を読み込み、ツリーノードにダンプする
説明
この関数は、渡された引数に応じて2つの関数にオーバーロードされます。最初の関数(文字列を渡した場合)は廃止されました。代わりにexcelrangereadnum()とexcelrangereadstr()を使用してください。
2番目の関数(ツリーノードを渡した場合)はExcelのある範囲を読み込み、その範囲に含まれるすべてのデータをターゲットのツリーノードに割り当てます。ツリーノードにバンドルデータが存在する場合、Excelデータはバンドルに設定されます。それ以外の場合、ターゲットのツリーノードの下にサブノードが挿入されます。Excelのデータはこのサブノードに文字列または数値データとして、グローバルテーブルと同じ形式で設定されます。
範囲の原点は渡されたrowおよびcolにより指定され、2番目の数値のペアは範囲のサイズを指定します。これらのいずかに0が渡された場合、FlexSimはその方向のExcel範囲について、データが存在する範囲の境界を自動的に選択します。
flagsを渡すことで、Excelから正確に何を読み込むかを変更できます。flagsはEXCEL_DATA_AUTOMATIC、EXCEL_DATA_NUMBER、EXCEL_DATA_STRING、EXCEL_DATE_AS_NUM、EXCEL_USE_COLUMNHEADERS、EXCEL_USE_ROWHEADERSのいずれかです。
EXCEL_DATA_AUTOMATICは、Excelセルのデータタイプに応じて文字列または数値データを割り当てます。これはデフォルトの動作です。
EXCEL_DATA_NUMBERは、すべてのExcelデータを数値として読み込みます。
EXCEL_DATA_STRINGは、すべてのExcelデータを文字列として読み込みます。
EXCEL_DATE_AS_NUMは、Excel日付を、FlexSimで日付として読み込み可能な数値として読み込みます。それ以外の場合、データは文字列となります。
EXCEL_USE_COLUMNHEADERSは、データの最初の行をデータではなくテーブルの列の名前として使用します。
EXCEL_USE_ROWHEADERSは、データの最初の列をデータではなくテーブルの行の名前として使用します。
2番目の関数(ツリーノードを渡した場合)はExcelのある範囲を読み込み、その範囲に含まれるすべてのデータをターゲットのツリーノードに割り当てます。ツリーノードにバンドルデータが存在する場合、Excelデータはバンドルに設定されます。それ以外の場合、ターゲットのツリーノードの下にサブノードが挿入されます。Excelのデータはこのサブノードに文字列または数値データとして、グローバルテーブルと同じ形式で設定されます。
範囲の原点は渡されたrowおよびcolにより指定され、2番目の数値のペアは範囲のサイズを指定します。これらのいずかに0が渡された場合、FlexSimはその方向のExcel範囲について、データが存在する範囲の境界を自動的に選択します。
flagsを渡すことで、Excelから正確に何を読み込むかを変更できます。flagsはEXCEL_DATA_AUTOMATIC、EXCEL_DATA_NUMBER、EXCEL_DATA_STRING、EXCEL_DATE_AS_NUM、EXCEL_USE_COLUMNHEADERS、EXCEL_USE_ROWHEADERSのいずれかです。
EXCEL_DATA_AUTOMATICは、Excelセルのデータタイプに応じて文字列または数値データを割り当てます。これはデフォルトの動作です。
EXCEL_DATA_NUMBERは、すべてのExcelデータを数値として読み込みます。
EXCEL_DATA_STRINGは、すべてのExcelデータを文字列として読み込みます。
EXCEL_DATE_AS_NUMは、Excel日付を、FlexSimで日付として読み込み可能な数値として読み込みます。それ以外の場合、データは文字列となります。
EXCEL_USE_COLUMNHEADERSは、データの最初の行をデータではなくテーブルの列の名前として使用します。
EXCEL_USE_ROWHEADERSは、データの最初の列をデータではなくテーブルの行の名前として使用します。
例
treenode myTable = node ("Tools/GlobalTables/GlobalTable1>variables/data", model());
excelrangeread(myTable, 1, 1, 5, 0, EXCEL_DATA_AUTOMATIC | EXCEL_USE_COLUMNHEADERS);
アクティブなシートのセルA1からデータを読み込みます。最初の5行について、データが存在する列をすべて読み込みます。最初の行は、書き込み先のグローバルテーブルの列名に使用されます。したがって、Excelシートにデータの存在する列が10存在するなら、グローバルテーブルのデータ変数の下に合計40のノードが挿入されます。これらの各ノードは、対応するExcelセルのデータタイプになります。
excelrangeread(myTable, 1, 1, 5, 0, EXCEL_DATA_AUTOMATIC | EXCEL_USE_COLUMNHEADERS);
アクティブなシートのセルA1からデータを読み込みます。最初の5行について、データが存在する列をすべて読み込みます。最初の行は、書き込み先のグローバルテーブルの列名に使用されます。したがって、Excelシートにデータの存在する列が10存在するなら、グローバルテーブルのデータ変数の下に合計40のノードが挿入されます。これらの各ノードは、対応するExcelセルのデータタイプになります。
excelrangewrite (treenode source, num row, num col, num flags)
ソーステーブルノードからデータを読み込み、アクティブなExcelシートに置き込む
説明
この関数は、ソーステーブルノードのすべてのデータを、アクティブなExcelシートに書き込みます。ツリーノードにバンドルデータが存在する場合、バンドルデータを読み込んでシートに書き込みます。それ以外の場合、グローバルテーブルと同様に、データの存在する子ノードを探します。渡されるrowとcolは、Excelシートのどこからデータの書き込みを開始するかを指定します。常に、ソースノードのすべてのデータが書き込まれます。flagsを渡すと、ヘッダーの使用方法を変更できます。flagsに使用できるのは、EXCEL_USE_COLUMNHEADERSとEXCEL_USE_ROWHEADERSです。
EXCEL_USE_COLUMNHEADERSを使用すると、既存の列ヘッダーをExcelテーブルの別の行として書き込みます。
EXCEL_USE_ROWHEADERSを使用すると、既存の行ヘッダーをExcelテーブルの別の列として書き込みます。
EXCEL_USE_COLUMNHEADERSを使用すると、既存の列ヘッダーをExcelテーブルの別の行として書き込みます。
EXCEL_USE_ROWHEADERSを使用すると、既存の行ヘッダーをExcelテーブルの別の列として書き込みます。
例
treenode myTable = node("Tools/GlobalTables/GlobalTable1>variables/data", model());
excelrangewrite(myTable, 1, 1, EXCEL_USE_ROWHEADERS | EXCEL_USE_COLUMNHEADERS);
GlobalTable1のすべてのデータを取得し、アクティブなExcelシートのA1から始まるセルに書き込みます。実際のデータを書き込む前に、列ヘッダーの行と行ヘッダーの列があります。
excelrangewrite(myTable, 1, 1, EXCEL_USE_ROWHEADERS | EXCEL_USE_COLUMNHEADERS);
GlobalTable1のすべてのデータを取得し、アクティブなExcelシートのA1から始まるセルに書き込みます。実際のデータを書き込む前に、列ヘッダーの行と行ヘッダーの列があります。
excelread (num row, num col)
廃止、excelreadnum()、excelreadstr()、excelreadcell()のいずれかを使用すること
説明
このコマンドは廃止されました。代わりにexcelreadnum()、excelreadstr()、excelreadcell()のいずれかを使用してください。
例
excelwrite (str data, num row, num col)
廃止、excelwritenum()およびexcelwritestr()を使用すること
説明
このコマンドは廃止されました。代わりにexcelwritenum()とexcelwritestr()を使用してください。
例
executetablecell (str/node/num table, num row, num column)
廃止、Table.executeCell()またはTableの[]オペレーターを使用すること
説明
このコマンドは廃止されました。代わりにTable.executeCell()またはTableクラスの[]オペレーターを使用してください。
テーブルセルのテキストをFlexscriptとして実行します。
テーブルセルのテキストをFlexscriptとして実行します。
例
exp (num value)
exportfullhistory ([str filename, num scenario, num replication])
廃止
説明
このコマンドは廃止されました。実行中に収集された全履歴データをデータベース(.mdbファイル)に書き込みます。このコマンドにファイル名が渡された場合、その名前がデータベースに使用されます。ファイル名が渡されない場合、ユーザーはデータの保存先のファイルを指定するように求められます。ファイル(コマンドに渡された、またはダイアログで選択されたもの)が存在しない場合、新たに作成されます。
例
exportfullhistory("myrundata.mdb");
factorial (num value)
familycreate (obj familycontainer, str name)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
新しいファミリー(リレーショナル情報の編成に使用されるノードのリスト)を作成します。
新しいファミリー(リレーショナル情報の編成に使用されるノードのリスト)を作成します。
例
familycreate(item,"family1")
familydelete (obj familycontainer, str name)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
ファミリーを削除します。
ファミリーを削除します。
例
familydelete(item,"family1")
familymember (obj familycontainer, str name, num index)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
指定されたファミリーのメンバーへのポインターを返します。
指定されたファミリーのメンバーへのポインターを返します。
例
familymember(item,"family1",2)
familymemberadd (obj familycontainer, str name, obj member)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
指定されたfamilycontainerに新しいファミリーメンバーを追加します。
指定されたfamilycontainerに新しいファミリーメンバーを追加します。
例
familymemberadd(item,"family1",item.subnodes[1])
familymemberdel (obj familycontainer, str name, obj member)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
指定されたfamilycontainerからファミリーメンバーを削除します。
指定されたfamilycontainerからファミリーメンバーを削除します。
例
familymemberdel(item,"family1",item.subnodes[2])
familymemberqty (obj familycontainer, str name)
説明
このコマンドは廃止されました。代わりにGroupクラスを使用してください。
指定されたファミリーのサイズを返します。
指定されたファミリーのサイズを返します。
例
familymemberqty(item,"family1")
fillarray (array thearray, num/treenode/string val1[, num/treenode/string val2, ...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。配列リテラルを使用して配列を構築するには、Arrayクラスを使用してください。Array arr = [1, 2, 3];
ローカル配列に値を入力します。
ローカル配列に値を入力します。
例
findmatch (num nr, num matchexpression[, returnexpression = count, num reverseorder = 0])
説明
定義された回数だけ一致テストを実行し、一致が見つかった場合は、その一致と関連付けられたユーザ定義可能な値を返します。一致の式と戻り値の式では、チェックの反復の何回目かを「count」を使用して判定できます。これを使用して、何かのリストを検索し、一致するアイテムや条件を探すことができます。呼び出しにreturnexpressionが含まれていない場合、findmatch()は一致の式に関連付けられているcountを返します。一致が見つからなかった場合、findmatch()は0を返します。reverseorderが1なら、countにnrを最初に代入し、次にnr - 1を代入し、以下1まで逆順にカウントします。returnexpressionが指定されていない場合、findmatchは見つかった一致に関連付けられているcountを返します。
例
int portNr = findmatch(current.outObjects.length, current.outObjects[count].subnodes.length < 5);
この例は、currentの出力ポートに接続されている、コンテンツが5より小さい最初のオブジェクトに対応する出力ポート番号を返します。
treenode object = findmatch(current.outObjects.length, current.outObjects[count].subnodes.length < 5, current.outObjects[count]);
この例は前の例とほぼ同じですが、関連付けられているポート番号ではなくオブジェクト自体を返します。
int item2Rank = findmatch(current.subnodes.length, current.subnodes[count].type == 2);
この例は、currentのキューで見つかった、アイテムタイプが2である最初のアイテムのランク番号を返します。
この例は、currentの出力ポートに接続されている、コンテンツが5より小さい最初のオブジェクトに対応する出力ポート番号を返します。
treenode object = findmatch(current.outObjects.length, current.outObjects[count].subnodes.length < 5, current.outObjects[count]);
この例は前の例とほぼ同じですが、関連付けられているポート番号ではなくオブジェクト自体を返します。
int item2Rank = findmatch(current.subnodes.length, current.subnodes[count].type == 2);
この例は、currentのキューで見つかった、アイテムタイプが2である最初のアイテムのランク番号を返します。
findmax (num nr, num valueexpression[, returnexpression = maxvalue, num criterion = true, num reverseorder = 0])
説明
式を繰り返し評価し、見つかった最大値、またはその最大値に関連付けられているユーザー定義可能な戻り値を返します。値の式、戻り値の式、およひ基準では、チェックの反復の何回目かを「count」を使用して判定できます。戻り値の式が定義されていない場合、見つかった最大値が返されます。また、無効な値を除外するための基準を指定できます。基準が定義されており、基準を満たす値が存在しない場合、0が返されます。
例
double latestCreation = findmax(current.subnodes.length, getcreationtime(current.subnodes[count]));
この例は、currentに含まれるすべてのアイテムの最大作成時間を返します。
int largestQueuePortNr = findmax(current.inObjects.length, current.inObjects[count].subnodes.length;
この例は、アイテムの最も大きなキューを持つオブジェクトに関連付けられている入力ポート番号を返します。
int largestQueuePortNr = findmax(current.inObjects.length, current.inObjects[count].subnodes.length, count, getitemstate(current.inObjects[count].first) == FR_STATE_READY);
この例は前の例とほぼ同じですが、上流オブジェクトの最初のアイテムがリリースされているという条件が追加されています。
この例は、currentに含まれるすべてのアイテムの最大作成時間を返します。
int largestQueuePortNr = findmax(current.inObjects.length, current.inObjects[count].subnodes.length;
この例は、アイテムの最も大きなキューを持つオブジェクトに関連付けられている入力ポート番号を返します。
int largestQueuePortNr = findmax(current.inObjects.length, current.inObjects[count].subnodes.length, count, getitemstate(current.inObjects[count].first) == FR_STATE_READY);
この例は前の例とほぼ同じですが、上流オブジェクトの最初のアイテムがリリースされているという条件が追加されています。
findmin (num nr, num valueexpression[, returnexpression = maxvalue, num criterion = true, num reverseorder = 0])
説明
式を繰り返し評価し、見つかった最小値、またはその最小値に関連付けられているユーザー定義可能な戻り値を返します。findmin()はfindmax()とほぼ同じですが、最大値ではなく最小値を探します。詳細については、findmax()のドキュメントを参照してください。
例
findmax()を参照
first (node container)
floor (num num)
fmod (num value1, num value2)
forobjecthighlightedin (obj view) { }
説明
このコマンドは廃止されました。代わりにselectedobject()を使用してください。
選択されたビューで、選択された(赤色)および強調表示された(黄色)ノードについて繰り返し処理を行います。ループ内で「a」を使用し、選択および強調表示されたノードを参照します。
選択されたビューで、選択された(赤色)および強調表示された(黄色)ノードについて繰り返し処理を行います。ループ内で「a」を使用し、選択および強調表示されたノードを参照します。
例
forobjecthighlightedin(sv())
{
pt(a.name); pr();
}
モデルの最初のレベルに存在する、選択および強調表示されたノードの名前を出力コンソールに表示します。
{
pt(a.name); pr();
}
モデルの最初のレベルに存在する、選択および強調表示されたノードの名前を出力コンソールに表示します。
forobjectlayerunder (node container) { }
説明
このコマンドは廃止されました。代わりにfor()またはwhile()コマンドを使用してください。
containerとして指定されたノードの直下にあるツリーレイヤーの各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectlayerunder()コマンドはflexscriptでのみ使用でき、C++では使用できません。
containerとして指定されたノードの直下にあるツリーレイヤーの各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectlayerunder()コマンドはflexscriptでのみ使用でき、C++では使用できません。
例
forobjectlayerunder(model())
{
pt(a.name); pr();
}
モデルの最初のレベルに存在するすべてのオブジェクトの名前を、出力コンソールに表示します。
{
pt(a.name); pr();
}
モデルの最初のレベルに存在するすべてのオブジェクトの名前を、出力コンソールに表示します。
forobjectsbefore (node thenode) { }
説明
このコマンドは廃止されました。代わりにfor()またはwhile()コマンドを使用してください。
thenodeとして指定されたオブジェクトと同じレイヤーに属し、オブジェクトのランクと同じ、またはより小さいランク値を持つ各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectsbefore()コマンドはflexscriptでのみ使用でき、C++では使用できません。
thenodeとして指定されたオブジェクトと同じレイヤーに属し、オブジェクトのランクと同じ、またはより小さいランク値を持つ各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectsbefore()コマンドはflexscriptでのみ使用でき、C++では使用できません。
例
forobjectsbefore(model.subnodes[5]))
{
pt(a.name); pr();
}
モデルの最初にある5つのオブジェクトの名前を、出力コンソールに表示します。
{
pt(a.name); pr();
}
モデルの最初にある5つのオブジェクトの名前を、出力コンソールに表示します。
forobjectsbehind (node thenode) { }
説明
このコマンドは廃止されました。代わりにfor()またはwhile()コマンドを使用してください。
thenodeとして指定されたオブジェクトと同じレイヤーに属し、オブジェクトのランクと同じ、またはより大きいランク値を持つ各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectsbehind()コマンドはflexscriptでのみ使用でき、C++では使用できません。
thenodeとして指定されたオブジェクトと同じレイヤーに属し、オブジェクトのランクと同じ、またはより大きいランク値を持つ各ノードに対して、コードブロックを実行します。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjectsbehind()コマンドはflexscriptでのみ使用でき、C++では使用できません。
例
forobjectsbehind(model.subnodes[5])
{
pt(a.name); pr();
}
モデルの6番目から始めて、それ以後のオブジェクトの名前を、出力コンソールに表示します。
{
pt(a.name); pr();
}
モデルの6番目から始めて、それ以後のオブジェクトの名前を、出力コンソールに表示します。
forobjectselectionset (node container) { }
説明
このコマンドは廃止されました。代わりに次のコードを使用してください。
for(int i =1; i<= container.subnodes.length; i++)
{
if(switch_selected(container.subnodes[i]))
{
pt(container.subnodes[i].name); pr();
}
}
container内で選択された各オブジェクトに対して、コマンド以後のブロックが一回ずつ実行されます。「a」コマンドの値は、繰り返し実行が行われる対象のオブジェクトへのポインターを返します。このコマンドは、C++では使用できません。
for(int i =1; i<= container.subnodes.length; i++)
{
if(switch_selected(container.subnodes[i]))
{
pt(container.subnodes[i].name); pr();
}
}
container内で選択された各オブジェクトに対して、コマンド以後のブロックが一回ずつ実行されます。「a」コマンドの値は、繰り返し実行が行われる対象のオブジェクトへのポインターを返します。このコマンドは、C++では使用できません。
例
forobjectselectionset(library()) { pt(a.name); pr(); }
ライブラリツリーで現在選択されているすべてのオブジェクトの名前を、出力コンソールに表示します。
ライブラリツリーで現在選択されているすべてのオブジェクトの名前を、出力コンソールに表示します。
ge (num value1, num value2)
廃止、>=オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに>=オペレーターを使用してください。
例
get (node thenode)
getcolorcomponent (obj object, num index)
getdatatype (thing)
getinput (obj involved)
getitemtype (obj object)
廃止、ラベルを使用すること
説明
このコマンドは廃止されました。代わりにラベルを使用してください。
フローアイテムのitemtype値を返します。
フローアイテムのitemtype値を返します。
例
getitemtype(so())
getlabel (obj node, str/num label)
廃止、treenode.LabelNameを使用すること
説明
例
getlabelnum (obj node, str/num label)
廃止、treenode.LabelNameを使用すること
説明
例
getlabelstr (obj node, str/num label)
廃止、treenode.LabelNameを使用すること
説明
例
getmodelunitnum (num querytype)
説明
このコマンドは廃止されました。代わりにgetmodelunit()を使用してください。
例
getmodelunitstr (num querytype)
説明
このコマンドは廃止されました。代わりにgetmodelunit()を使用してください。
現在のモデル単位の名前または略語を返します。
現在のモデル単位の名前または略語を返します。
例
getmoverecord (num record)
廃止
説明
このコマンドは廃止されました。全履歴レポート用に記録された移動レコードを返します。全履歴が有効な場合、フローアイテムがオブジェクトから別のオブジェクトに移動するごとに、移動レコードが作成されます。この関数に渡されるパラメータは、ユーザーが取得するレコードの番号(1から開始)です。このコマンドがC++で呼び出された場合、戻り値はMoveRecord*です。このコマンドがFlexScriptで呼び出された場合、戻り値はintに代入できます。
例
getnummoverecords()の例を参照してください。
getmoverecordvalue (num record, num value)
廃止
説明
このコマンドは廃止されました。関数の最初のパラメータとして渡された移動レコードから、値の1つを返します。このレコードは、getmoverecord()への呼び出しで返される戻り値です。この関数の2番目のパラメータとして渡される値は、移動レコードのどの値をユーザーが取得するかを示します。
0 = レコードID。これは、移動テーブルのレコードの行番号です。
1 = レコードに移動が記録されたフローアイテムのItemID。
2 = フローアイテムが移動した時間。
3 = フローアイテムの移動元のオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
4 = フローアイテムの移動先のオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
5 = フローアイテムが移動した時点でのアイテムタイプ。
0 = レコードID。これは、移動テーブルのレコードの行番号です。
1 = レコードに移動が記録されたフローアイテムのItemID。
2 = フローアイテムが移動した時間。
3 = フローアイテムの移動元のオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
4 = フローアイテムの移動先のオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
5 = フローアイテムが移動した時点でのアイテムタイプ。
例
getnummoverecords()の例を参照してください。
getname (node thenode)
getnodename (node thenode)
getnodenum (node thenode)
getnodestr (node thenode)
getnummoverecords ()
廃止
説明
このコマンドは廃止されました。全履歴レポート用に収集された移動レコードの数を返します。モデルがリセットされるとレコードは削除されるため、モデルの実行前は0が返されます。全履歴が有効でない場合、0が返されます。
例
// 記録された移動レコードを出力する
for (int rec = 1; rec <= getnummoverecords(); rec++)
{
int record = getmoverecord(rec);
pd(getmoverecordvalue(record,0)); pt(" ");
pd(getmoverecordvalue(record,1)); pt(" ");
pf(getmoverecordvalue(record,2)); pt(" ");
pt(getmoverecordvalue(record,3).name); pt(" ");
pt(getmoverecordvalue(record,4).name); pt(" ");
pd(getmoverecordvalue(record,5)); pt(" ");
}
for (int rec = 1; rec <= getnummoverecords(); rec++)
{
int record = getmoverecord(rec);
pd(getmoverecordvalue(record,0)); pt(" ");
pd(getmoverecordvalue(record,1)); pt(" ");
pf(getmoverecordvalue(record,2)); pt(" ");
pt(getmoverecordvalue(record,3).name); pt(" ");
pt(getmoverecordvalue(record,4).name); pt(" ");
pd(getmoverecordvalue(record,5)); pt(" ");
}
getnumstaterecords ()
廃止
説明
このコマンドは廃止されました。全履歴レポート用に収集された状態変化レコードの数を返します。モデルがリセットされるとレコードは削除されるため、モデルの実行前は0が返されます。全履歴が有効でない場合、0が返されます。
例
// 記録された状態変化レコードを出力する
for (int rec = 1; rec <= getnumstaterecords(); rec++)
{
int record = getstaterecord(rec);
pd(getstaterecordvalue(record,0)); pt(" ");
pf(getstaterecordvalue(record,1)); pt(" ");
pd(getstaterecordvalue(record,2)); pt(" ");
pt(getstaterecordvalue(record,3).name); pr();
}
for (int rec = 1; rec <= getnumstaterecords(); rec++)
{
int record = getstaterecord(rec);
pd(getstaterecordvalue(record,0)); pt(" ");
pf(getstaterecordvalue(record,1)); pt(" ");
pd(getstaterecordvalue(record,2)); pt(" ");
pt(getstaterecordvalue(record,3).name); pr();
}
getobjectimageindex (obj object)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
objectのベースに現在割り当てられているbmpまたはjpeg画像のインデックス番号を返します。
objectのベースに現在割り当てられているbmpまたはjpeg画像のインデックス番号を返します。
例
getobjectimageindex(item);
getquerycolcount ()
getquerymatchcount ()
getquerymatchtablerow (str/num table, num matchRow)
廃止、Table.query()を使用すること
説明
このコマンドは廃止されました。代わりにTable.query()を使用してください。
最後のquery()結果で一致する行に関連付けられている、ソーステーブルの行番号を返します。
table - 文字列の場合、FROMステートメントで定義されたテーブルの名前です。エイリアスを使用した場合、テーブルのエイリアスを使用します。数値の場合、FROMステートメントのテーブルの1から始まるインデックスです。クエリにテーブルが1つしか存在しない場合、1を使用します。複数のテーブルの場合、FROMの最初のテーブルが1、2番目が2の順序です。
matchRow - クエリの結果テーブルの行で、1から始まります。
SELECT句の中でMIN()、MAX()、AVG()などの集計関数を使用している場合、このコマンドは動作しないことに注意してください。集計関数が使用されている場合、このコマンドは単にソーステーブル内の行数を返します。
最後のquery()結果で一致する行に関連付けられている、ソーステーブルの行番号を返します。
table - 文字列の場合、FROMステートメントで定義されたテーブルの名前です。エイリアスを使用した場合、テーブルのエイリアスを使用します。数値の場合、FROMステートメントのテーブルの1から始まるインデックスです。クエリにテーブルが1つしか存在しない場合、1を使用します。複数のテーブルの場合、FROMの最初のテーブルが1、2番目が2の順序です。
matchRow - クエリの結果テーブルの行で、1から始まります。
SELECT句の中でMIN()、MAX()、AVG()などの集計関数を使用している場合、このコマンドは動作しないことに注意してください。集計関数が使用されている場合、このコマンドは単にソーステーブル内の行数を返します。
例
getqueryvalue (num row, num/str col)
getrank (node thenode)
gets (node thenode)
getstatenum (obj object [, num stateprofilenr])
getstaterecord (num record)
廃止
説明
このコマンドは廃止されました。全履歴レポート用に記録された状態変化レコードを返します。全履歴が有効なとき、オブジェクトの状態が変化するごとに状態変化レコードが作成されます。この関数に渡されるパラメータは、ユーザーが取得するレコードの番号(1から開始)です。このコマンドがC++で呼び出された場合、戻り値はStateRecord*です。このコマンドがFlexScriptで呼び出された場合、戻り値はintに代入できます。
例
getnumstaterecords()の例を参照してください。
getstaterecordvalue (num record, num value)
廃止
説明
このコマンドは廃止されました。関数の最初のパラメータとして渡された状態変化レコードから、値の1つを返します。このレコードは、getstaterecord()への呼び出しで返される戻り値です。この関数の2番目のパラメータとして渡される値は、状態変化レコードのどの値をユーザーが取得するかを示します。
0 = レコードID。これは、移動テーブルのレコードの行番号です。
1 = 状態変化の時間。
2 = オブジェクトの変化後の状態。
3 = 状態が変化したオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
0 = レコードID。これは、移動テーブルのレコードの行番号です。
1 = 状態変化の時間。
2 = オブジェクトの変化後の状態。
3 = 状態が変化したオブジェクト。この値はintとして返され、tonode()を使用してtreenodeに変換する必要があります。
例
getnumstaterecords()の例を参照してください。
getstatestr (obj object)
gettablecell (str/node/num table, num row, num column)
gettablecols (str/node/num table)
gettableheader (string/num/node table, num row/col, num rowcolnr)
廃止、Table.getColHeader()またはTable.getRowHeader()を使用すること
説明
例
gettablenum (str/node/num table, num row, num col)
廃止、Tableの[]オペレーターを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスの[]オペレーターを使用してください。
テーブルのセルの数値を取得します。
テーブルのセルの数値を取得します。
例
gettablerows (str/node/num table)
gettablestr (str/node/num table, num row, num col)
廃止、Tableの[]オペレーターを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスの[]オペレーターを使用してください。
テーブルのセルのテキスト値を取得します。
テーブルのセルのテキスト値を取得します。
例
gettrackedvariable (str/node trackedvar [, num valtype] )
廃止、TrackedVariableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTrackedVariableクラスを使用してください。
例
getvartype (var)
glBegin (num primitive)
廃止、mesh() APIを使用すること
説明
このコマンドは廃止されました。使用してはいけません。代わりにmesh() APIを使用してください。
例
glColor3d (num red {0-1}, num green {0-1}, num blue {0-1})
廃止、fglColor()を使用すること
説明
このコマンドは廃止されました。代わりにfglColor()を使用してください。
例
glColor4d (num red {0-1}, num green {0-1}, num blue {0-1}, num alpha {0-1})
廃止、fglColor()を使用すること
説明
このコマンドは廃止されました。代わりにfglColor()を使用してください。
例
glDisable (num setting)
廃止、fglDisable()を使用すること
説明
このコマンドは廃止されました。代わりにfglDisable()を使用してください。
例
glEnable (num setting)
廃止、fglEnable()を使用すること
説明
このコマンドは廃止されました。代わりにfglEnableを使用してください。
例
glEnd ()
廃止、mesh() APIを使用すること
説明
このコマンドは廃止されました。使用してはいけません。代わりにmesh() APIを使用してください。
例
glLoadIdentity ()
廃止、fglLoadIdentity()を使用すること
説明
このコマンドは廃止されました。代わりにfglLoadIdentity()を使用してください。
例
glMatrixMode (num mode)
廃止、fglMatrixMode()を使用すること
説明
このコマンドは廃止されました。代わりにfglMatrixMode()を使用してください。
例
glNormal3d (num x, num y, num z)
廃止、fglNormal()を使用すること
説明
このコマンドは廃止されました。代わりにfglNormal()を使用してください。
例
glNormal3d(1,0,0);
globallist (str listName)
廃止、List("GlobalListName")を使用すること
説明
このコマンドは廃止されました。代わりにList("GlobalListName")を使用してください。
グローバルリストを名前で参照します。
グローバルリストを名前で参照します。
例
glPopAttrib ()
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
glPopMatrix ()
廃止、fglPopMatrix()を使用すること
説明
このコマンドは廃止されました。代わりにfglPopMatrix()を使用してください。
例
glPushAttrib (num attribsetting)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
glPushMatrix ()
廃止、fglPushMatrix()を使用すること
説明
このコマンドは廃止されました。代わりにfglPushMatrix()を使用してください。
例
glRotated (num degrees, num x, num y, num z)
廃止、fglRotate()を使用すること
説明
このコマンドは廃止されました。代わりにfglRotate()を使用してください。
例
glScaled (num x, num y, num z)
廃止、fglScale()を使用すること
説明
このコマンドは廃止されました。代わりにfglScale()を使用してください。
例
glTexCoord2d (num x 0-1, num y 0-1)
廃止、mesh() APIを使用すること
説明
このコマンドは廃止されました。使用してはいけません。代わりにmesh() APIを使用してください。
例
glTranslated (num x, num y, num z)
廃止、fglTranslate()を使用すること
説明
このコマンドは廃止されました。代わりにfglTranslate()を使用してください。
例
glVertex3d (num x, num y, num z)
廃止、mesh() APIを使用すること
説明
このコマンドは廃止されました。使用してはいけません。代わりにmesh() APIを使用してください。
例
groupaddmember (str group, obj member)
groupmember (str group, num member)
廃止、Group[]を使用すること
説明
このコマンドは廃止されました。代わりにGroup[]を使用してください。
グループメンバーへの参照を取得します。
グループメンバーへの参照を取得します。
例
groupnummembers (str group)
groupremovemember (str group, num/obj member)
廃止、Group.removeMember()を使用すること
説明
例
gt (num value1, num value2)
廃止、>オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに>オペレーターを使用してください。
例
helpcommands (node destnode, num what, str command)
説明
開発者向けです。コマンドについての情報の取得に使用します。パラメータ3にコマンド名を入力します。戻り値はdestnodeの文字列データにコピーされます。
「what」は、どの情報が必要なのかを次のように定義します。
1 - コマンドのドキュメントを含むxmlフラグメント文字列を返します。
「what」は、どの情報が必要なのかを次のように定義します。
1 - コマンドのドキュメントを含むxmlフラグメント文字列を返します。
例
helpcommands()
hidelabel (obj object[, num off/on])
廃止、switch_hidelabel()を使用すること
説明
このコマンドは廃止されました。代わりにswitch_hidelabel()を使用してください。
このコマンドは、指定されたobjectについて、名前と基本統計を画面上で表示/非表示にします。値が1なら表示、0なら非表示になります。オブジェクトの名前と統計が非表示のとき、どのビューウィンドウにも表示されません。ビューウィンドウには、ビューのすべてのオブジェクトについて、このコネクタ表示を制御する属性もあります。
このコマンドは、指定されたobjectについて、名前と基本統計を画面上で表示/非表示にします。値が1なら表示、0なら非表示になります。オブジェクトの名前と統計が非表示のとき、どのビューウィンドウにも表示されません。ビューウィンドウには、ビューのすべてのオブジェクトについて、このコネクタ表示を制御する属性もあります。
例
Hidelabel(current,0);
currentで参照されるオブジェクトの名前と統計を表示しないよう設定します。
currentで参照されるオブジェクトの名前と統計を表示しないよう設定します。
hideports (obj object[, num off/on])
廃止、switch_hideconnectors()を使用すること
説明
このコマンドは廃止されました。代わりにswitch_hideconnectors()を使用してください。
このコマンドは、指定されたobjectについて、ポートと接続を表示/非表示に設定します。値が1なら表示、0なら非表示になります。オブジェクトのポートと接続が非表示のとき、どのビューウィンドウにも表示されません。
このコマンドは、指定されたobjectについて、ポートと接続を表示/非表示に設定します。値が1なら表示、0なら非表示になります。オブジェクトのポートと接続が非表示のとき、どのビューウィンドウにも表示されません。
例
hideports(current,1);
currentオブジェクトのポートと接続をすべてのビューウィンドウに表示するよう設定します。
currentオブジェクトのポートと接続をすべてのビューウィンドウに表示するよう設定します。
inc (node thenode, num amount)
廃止、+=オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに+=オペレーターを使用してください。myNode.value += 2;
ノードの値を定義された数値だけ増やします。
ノードの値を定義された数値だけ増やします。
例
inc(current.mylabel,1)
inittrackedvariable (node theNode, num type[, num startValue, num flags])
廃止、TrackedVariableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTrackedVariableクラスを使用してください。
例
inobject (obj object, num inputportnum)
installpackage (str path+filename)
廃止、ユーザーライブラリを使用すること
説明
このコマンドは廃止されました。代わりにユーザーライブラリを使用してください。
サービスパック(.fpk)をインストールします。
サービスパック(.fpk)をインストールします。
例
installpackage("C:/mypak.fpk")
item <括弧なし>
説明
このコマンドは廃止されました。このコマンドは、今後setitemコマンドとともに特殊コマンドとして使用してはいけません。代わりに、treenode変数タイプをアイテムとして宣言し、コード内で他の変数タイプと同様にアイテムを使用してください。
例
treenode item = model().subnodes[3];
pt(item.name);
モデル内で3にランクされるオブジェクトをitemに設定し、出力コンソールにその名前を表示します。
pt(item.name);
モデル内で3にランクされるオブジェクトをitemに設定し、出力コンソールにその名前を表示します。
iterate (num start, num end, num step) {}
廃止、for()またはwhile()コマンドを使用すること
説明
このコマンドは廃止されました。代わりにfor()またはwhile()コマンドを使用してください。
カウンターの値をstartからendまで、step単位で増やしながら、次に続く{}ブロックを繰り返し実行します。countコマンドを使用して、繰り返しごとに現在のカウンターの値にアクセスできます。countの戻り値は、現在何回目の反復が実行されているかによって異なります。
カウンターの値をstartからendまで、step単位で増やしながら、次に続く{}ブロックを繰り返し実行します。countコマンドを使用して、繰り返しごとに現在のカウンターの値にアクセスできます。countの戻り値は、現在何回目の反復が実行されているかによって異なります。
例
iterate(1,9,2)
{
pd(count);pr();
}
次の数値を出力コンソールに表示します:1,3,5,7,9
{
pd(count);pr();
}
次の数値を出力コンソールに表示します:1,3,5,7,9
label (obj object, str/num label)
last (node container)
le (num value1, num value2)
廃止、<=オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに<=オペレーターを使用してください。
例
listbackorders (obj list[, var partitionId])
廃止、List.backOrders()を使用すること
説明
例
listentries (obj list[, var partitionId])
listinlist (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
リストに値が出現する場所のインデックス。この関数は長さqtyのリストを検索し、値valが出現する位置を返します。
リストに値が出現する場所のインデックス。この関数は長さqtyのリストを検索し、値valが出現する位置を返します。
例
listinlist(5,3,2,1,2,3,4)
5つの数値のリストで、3は4番目の数値なので、インデックス番号4が返されます。
5つの数値のリストで、3は4番目の数値なので、インデックス番号4が返されます。
listmax (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
最も大きな値のインデックス。この関数は長さqtyのリストを検索し、最も大きな値が出現する位置を返します。
最も大きな値のインデックス。この関数は長さqtyのリストを検索し、最も大きな値が出現する位置を返します。
例
listmax(5,2,1,2,3,4)
5つの数値のリストで、4が最も大きな値なので、5が返されます。
5つの数値のリストで、4が最も大きな値なので、5が返されます。
listmaximum (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
最大値。この関数は長さqtyのリストを検索し、最も大きな値を返します。
最大値。この関数は長さqtyのリストを検索し、最も大きな値を返します。
例
listmaximum(5,2,1,2,3,4)
リストで最も大きな値が4なので、4が返されます。
リストで最も大きな値が4なので、4が返されます。
listmean (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
値の平均値。この関数は、長さqtyのリストから値の平均値を返します。
値の平均値。この関数は、長さqtyのリストから値の平均値を返します。
例
listmean(5,2,1,2,3,4)
2.5が返されます。
2.5が返されます。
listmin (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
最も小さな値のインデックス。この関数は長さqtyのリストを検索し、最も小さな値が出現する位置を返します。
最も小さな値のインデックス。この関数は長さqtyのリストを検索し、最も小さな値が出現する位置を返します。
例
listmin(5,2,1,2,3,4)
リストで最も小さな値が1で、2番目の値なので、2が返されます。
リストで最も小さな値が1で、2番目の値なので、2が返されます。
listminimum (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
最小値。この関数は長さqtyのリストを検索し、最も小さな値を返します。
最小値。この関数は長さqtyのリストを検索し、最も小さな値を返します。
例
listminimum(5,2,1,2,3,4)
リストで最も小さな値が1なので、1が返されます。
リストで最も小さな値が1なので、1が返されます。
listmul (num qty, num val [, num a,...])
廃止、*オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに*オペレーターを使用してください。
リストの積。この関数は、長さqtyのリストに含まれるすべての値の積を返します。
リストの積。この関数は、長さqtyのリストに含まれるすべての値の積を返します。
例
listmul(5,2,1,2,3,4)
値48を返します。
値48を返します。
listpull (str/obj list, str/node query, num requestNum [, num requireNum, str/node/num puller, str/node/num partitionId, num flags])
listpush (str/obj list [, str/node/num pushVal, str/node/num partitionId, ...])
listremove (obj entryOrBackOrder)
廃止、List.backOrders()[backOrderNum].remove()またはList.entries()[enterNum].remove()を使用すること
説明
このコマンドは廃止されました。代わりにList.backOrders()[backOrderNum].remove()またはList.entries()[entryNum].remove()を使用してください。
所有しているリストからエントリまたはバックオーダーを削除します。
所有しているリストからエントリまたはバックオーダーを削除します。
例
listsub (num qty, num val [, num a,...])
廃止、-オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに-オペレーターを使用してください。
リストの減算。この関数は、長さqtyのリストについて最初の値を取得してから、以後のすべての値を減算し、結果を返します。
リストの減算。この関数は、長さqtyのリストについて最初の値を取得してから、以後のすべての値を減算し、結果を返します。
例
listsub(5,2,1,2,3,4)
listsum (num qty, num val [, num a,...])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりに+オペレーターを使用してください。
値の合計。この関数は、長さqtyのリストの値すべての合計を返します。
値の合計。この関数は、長さqtyのリストの値すべての合計を返します。
例
listsum(5,2,1,2,3,4)
loadsound (str path+filename)
廃止、soundload()を使用すること
説明
このコマンドは廃止されました。代わりにsoundload()を使用してください。
ディスク上のサウンドファイルがFlexSimにロードされ、メディアリストに記録されます。FlexSimのメディアリストは、ロードされたすべてのサウンドのリストを保持します。それぞれのサウンドには、対応する名前とインデックスが存在します。このコマンドは、ロードされたサウンドに対応するインデックスを返します。このサウンドは.wavファイルの必要があります。
ディスク上のサウンドファイルがFlexSimにロードされ、メディアリストに記録されます。FlexSimのメディアリストは、ロードされたすべてのサウンドのリストを保持します。それぞれのサウンドには、対応する名前とインデックスが存在します。このコマンドは、ロードされたサウンドに対応するインデックスを返します。このサウンドは.wavファイルの必要があります。
例
int applauseindex = loadsound("c:/My Music/APPLAUSE.WAV");
local (num index)
廃止、ローカル変数を使用すること
説明
このコマンドは廃止されました。代わりに、treenode、int、double、stringなどのローカル変数を使用してください。
インデックス付きローカル変数をツリーノードとして、参照を取得します。いくつのローカル変数を使用するか、およびどのデータタイプを保有するかは、localarray()を使用して定義する必要があります。flexscriptでのみ使用できます。
インデックス付きローカル変数をツリーノードとして、参照を取得します。いくつのローカル変数を使用するか、およびどのデータタイプを保有するかは、localarray()を使用して定義する必要があります。flexscriptでのみ使用できます。
例
setnodenum(local(1),4);
ローカル配列の最初の変数を4に設定します。
ローカル配列の最初の変数を4に設定します。
localarray (num qty[, num datatype])
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArrayクラスを使用してください。
指定された数のローカル変数を持つ、汎用ローカル配列を割り当てます。
タイプは次のいずれかです:1 = num、2 = str、3 = coupling、4 = objflexscriptでのみ使用できます。
指定された数のローカル変数を持つ、汎用ローカル配列を割り当てます。
タイプは次のいずれかです:1 = num、2 = str、3 = coupling、4 = objflexscriptでのみ使用できます。
例
localarray(1,4)
log10 (num value)
lognormal (num location, num normalmean, num normalstdev[, num stream])
対数正規分布からランダムなサンプルを返す
説明
lognormal()とlognormal2()は類似の関数ですが、パラメータの定義が異なります。lognormal()は、wikipediaや他のサイトで定義されているパラメータ定義を使用します。lognormal2()は、Expertfitの最新版で定義されているパラメータを使用します。本質的に、パラメータは次のように変換できます。
lognormal( location, normalmean, normalstdev ) = lognormal2( location, Math.exp( normalmean ), normalstdev )
lognormal2( location, scale, shape ) = lognormal( location, Math.log( scale ), shape ) (Math.exp(x)はeのx乗で、Math.log(x)はxの自然対数です)。
正しい分布を使用していることを確認してください。誤った分布を使用すると、不適切なシミュレーション結果が得られることがあります。
lognormal( location, normalmean, normalstdev, stream )は連続確率分布です。
入力:
location : ( - ∞, ∞ )
(Math.exp( normalmean ) > 0)となるようなnormalmean
(normalstdev > 0)となるようなnormalstdev
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかを参照します。
出力:
range = ( location , ∞ )
mean = location + Math.exp( normalmean + normalstdev²⁄ 2)
variance = Math.exp( 2*normalmean + normalstdev² ) [ Math.exp( normalstdev² ) − 1 ]
確率密度関数:
可能な用途:
一部のタスクを実行する時間のモデル化、および多数の他の数量の積となる数量をモデル化するため使用されます。データがない場合に概略モデルとしても使用できます。
コメント:
対数正規分布の確率密度は、normalstdev > 1についてはgamma( normalstdev, normalmean )およびweibull( normalstdev, normalmean )の密度に近い形となりますが、x=0付近で大きなスパイクが発生することがあり、多くの場合にはこれが有用です。
lognormal( location, normalmean, normalstdev ) = lognormal2( location, Math.exp( normalmean ), normalstdev )
lognormal2( location, scale, shape ) = lognormal( location, Math.log( scale ), shape ) (Math.exp(x)はeのx乗で、Math.log(x)はxの自然対数です)。
正しい分布を使用していることを確認してください。誤った分布を使用すると、不適切なシミュレーション結果が得られることがあります。
lognormal( location, normalmean, normalstdev, stream )は連続確率分布です。
入力:
location : ( - ∞, ∞ )
(Math.exp( normalmean ) > 0)となるようなnormalmean
(normalstdev > 0)となるようなnormalstdev
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかを参照します。
出力:
range = ( location , ∞ )
mean = location + Math.exp( normalmean + normalstdev²⁄ 2)
variance = Math.exp( 2*normalmean + normalstdev² ) [ Math.exp( normalstdev² ) − 1 ]
確率密度関数:

可能な用途:
一部のタスクを実行する時間のモデル化、および多数の他の数量の積となる数量をモデル化するため使用されます。データがない場合に概略モデルとしても使用できます。
コメント:
対数正規分布の確率密度は、normalstdev > 1についてはgamma( normalstdev, normalmean )およびweibull( normalstdev, normalmean )の密度に近い形となりますが、x=0付近で大きなスパイクが発生することがあり、多くの場合にはこれが有用です。
例
lognormalmeanstdev (num mean, num stdev[, num stream])
対数正規分布からランダムなサンプルを返す
説明
このコマンドは、データが存在しないときlognormal2コマンドの代替として使用されます。平均と標準偏差を指定でき、コマンドはこれらのパラメータからlognormal2コマンド用の正しい場所、スケール、形状のパラメータを計算し、その分布からサンプルを返します。分布の形状は鐘型の曲線で、右側に妥当な長さのテール部があるよう事前定義されていることに注意してください。したがって、このコマンドはlognormal2コマンドほど柔軟ではありません。このコマンドは三角分布と同様に、データが存在せず、分布の平均値と標準偏差が判明しており、分布が右傾斜している(右側のテールの方が長い)と想定できるが、分布に一致する実際のデータセットが存在しない場合に使用します。詳細については、lognormal2を参照してください。lognormal2の分布を記述する図に関して、lognormalmeanstdevコマンドはnormalstdev/shapeに値0.75を使用して形状を定義します。分布の形状は固定されているため、平均値と標準偏差値によっては負の値が返される場合もあることに注意してください。
例
double cycletime = lognormalmeanstdev(10, 2);
この例は、平均値が10、標準偏差が2の右傾斜した対数正規分布に従うランダムな値を返します。
この例は、平均値が10、標準偏差が2の右傾斜した対数正規分布に従うランダムな値を返します。
lt (num value1, num value2)
廃止、<オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに<オペレーターを使用してください。
例
main ()
廃止、maintree()を使用すること
説明
このコマンドは廃止されました。代わりにmaintree()を使用してください。
メインツリーノードを取得します。これは、FlexSimの2つの主要なデータベースの1つです。「プロジェクトツリー」とも呼ばれます。他の主要なデータベースはビューツリーノードで、「ビューレイアウトツリー」とも呼ばれます。
メインツリーノードを取得します。これは、FlexSimの2つの主要なデータベースの1つです。「プロジェクトツリー」とも呼ばれます。他の主要なデータベースはビューツリーノードで、「ビューレイアウトツリー」とも呼ばれます。
例
main()
makearray (num qty)
廃止、Arrayクラスを使用すること
説明
このコマンドは廃止されました。代わりにArray(qty)を使用してください。Array array = Array(4);
ローカル配列を初期化します。
ローカル配列を初期化します。
例
max (num value1, num value2)
maxof (num value1, num value2)
min (num value1, num value2)
minof (num value1, num value2)
module (num type, node libnode)
廃止
説明
このコマンドは廃止されました。代わりに、バージョン4で提供されるDLL機能を使用してください。
dllプラグインで使用されます。タイプは次のいずれかです。
MOD_LOAD (1)
MOD_UNLOAD (2)
MOD_GETFUNCTION (3)
MOD_RUNFUNCTION (4)
dllプラグインで使用されます。タイプは次のいずれかです。
MOD_LOAD (1)
MOD_UNLOAD (2)
MOD_GETFUNCTION (3)
MOD_RUNFUNCTION (4)
例
module(MOD_UNLOAD,main.find("project/exec/dll/1"))
movetablecol (str/num/node table, num column, num newcolumn)
movetablerow (str/num/node table, num row, num newrow)
mul (num value1, num value2)
廃止、*オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに*オペレーターを使用してください。
aとbの積。value1*value2の数値演算の結果を返します。
aとbの積。value1*value2の数値演算の結果を返します。
例
double product = mul(3,4);
multisorttable (str/node/num table, num col1[, num col2, num col3, ...])
ne (num/node value1, num/node value2)
廃止、!=オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに!=オペレーターを使用してください。
例
next (obj object)
node (str relativepath[, obj startnode])
nodeadddata (node thenode, num type:num/str/ptr/obj)
nodedeldata (node thenode)
nodepoint (node a, node b)
nodetomodelpath (node thenode [, num nameflag=1])
nodetopath (node thenode [, num nameflag=0])
not (num/node value1)
廃止、!オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに!オペレーターを使用してください。
例
nrcp (obj object)
廃止、Object.centerObjects.lengthを使用すること
説明
例
nrip (obj object)
nrop (obj object)
廃止、Object.outObjects.lengthを使用すること
説明
例
ntravelto (obj traveler, obj spline, num endx, num endy, num endz, num vmax, num acc, num dec, num startspeed, num endspeed)
廃止、代わりにキネマティクスを使用すること
説明
このコマンドは廃止されました。代わりにキネマティクスを使用してください。
与えられたrzにオブジェクトを移動し、シミュレーションでの到着時間を返します。traveltoコマンドと似ていますが、開始および終了速度の定義が含まれます。TaskExecuterの開発に使用されます。
与えられたrzにオブジェクトを移動し、シミュレーションでの到着時間を返します。traveltoコマンドと似ていますが、開始および終了速度の定義が含まれます。TaskExecuterの開発に使用されます。
例
ntravelto(current, 0, 5, 8, 0, 1, 1, 1, 0, 1)
ntraveltoupdate (obj object)
廃止、代わりにキネマティクスを使用すること
説明
このコマンドは廃止されました。代わりにキネマティクスを使用してください。
ntravelto()コマンドが呼び出された後で、objectのrzを更新します。TaskExecuterのOnPreDrawで、位置を更新するため使用されます。
ntravelto()コマンドが呼び出された後で、objectのrzを更新します。TaskExecuterのOnPreDrawで、位置を更新するため使用されます。
例
ntraveltoupdate(current)
numtostring (num value[, num width, num precision])
objectconnect (obj object1, obj object2)
廃止、contextdragconnection()を使用すること
説明
このコマンドは廃止されました。代わりにcontextdragconnection()を使用してください。
2つのオブジェクトを接続し、必要なポートを追加します。必要ならobject1には出力ポートが、object2には入力が追加されます。その後でポート同士が接続されます。
2つのオブジェクトを接続し、必要なポートを追加します。必要ならobject1には出力ポートが、object2には入力が追加されます。その後でポート同士が接続されます。
例
connect(so(),so().next)
objectshapecode (obj object)
廃止、getshapeindex()を使用すること
説明
このコマンドは廃止されました。代わりにgetshapeindex()を使用してください。
オブジェクトのデフォルト形状のインデックスを取得します。FlexSimのメディアリストは、ロードされたすべての形状のリストを保持します。それぞれの形状には、対応する名前とインデックスが存在します。このコマンドは、オブジェクトのデフォルト形状に対応するインデックスを返します。
オブジェクトのデフォルト形状のインデックスを取得します。FlexSimのメディアリストは、ロードされたすべての形状のリストを保持します。それぞれの形状には、対応する名前とインデックスが存在します。このコマンドは、オブジェクトのデフォルト形状に対応するインデックスを返します。
例
objectshapecode(so())
objecttexcode (obj object)
廃止、getobjecttextureindex()を使用すること
説明
このコマンドは廃止されました。代わりにgetobjecttextureindex()を使用してください。
objectのデフォルト画像のインデックスを取得します。FlexSimのメディアリストは、ロードされたすべてのテクスチャ(画像)のリストを保持します。それぞれのテクスチャには、対応する名前とインデックスが存在します。このコマンドは、オブジェクトのデフォルトテクスチャ(画像)に対応するインデックスを返します。
objectのデフォルト画像のインデックスを取得します。FlexSimのメディアリストは、ロードされたすべてのテクスチャ(画像)のリストを保持します。それぞれのテクスチャには、対応する名前とインデックスが存在します。このコマンドは、オブジェクトのデフォルトテクスチャ(画像)に対応するインデックスを返します。
例
objecttexcode(current)
openflexsimchart ([str filename1] [,str filename2])
廃止
説明
このコマンドは廃止されました。
例
openglcolor (num red {0-1}, num green {0-1}, num blue {0-1}, num opacity {0-1})
廃止、fglColor()を使用すること
説明
このコマンドは廃止されました。代わりにfglColor()を使用してください。
例
opengllighting (num on/off)
廃止、fglEnable(GL_LIGHTING)およびfglDisable(GL_LIGHTING)を使用すること
説明
このコマンドは廃止されました。代わりにfglEnable(GL_LIGHTING)およびfglDisable(GL_LIGHTING)を使用してください。
例
openinput (obj object)
廃止、Object.input.open()を使用すること
説明
このコマンドは廃止されました。代わりにObject.input.open()を使用してください。
このコマンドは、以前にcloseinput()コマンドでブロックされたオブジェクトの入力のブロックを解除します。進入を許可する前に、入力ポート自体と入力全般を開く必要があります。モデラーは、senddelayedmessage()コマンドによりトリガーされたOnMessageフィールドを除いて、いかなるフィールドでもこのコマンドを使用しないことをお勧めします。これは、ポートを開くコマンドは多くの場合、トランジションイベントで行うべきでない複数の他の動作を引き起こすためです。このコマンドをresumeinput()と比較してください。
このコマンドは、以前にcloseinput()コマンドでブロックされたオブジェクトの入力のブロックを解除します。進入を許可する前に、入力ポート自体と入力全般を開く必要があります。モデラーは、senddelayedmessage()コマンドによりトリガーされたOnMessageフィールドを除いて、いかなるフィールドでもこのコマンドを使用しないことをお勧めします。これは、ポートを開くコマンドは多くの場合、トランジションイベントで行うべきでない複数の他の動作を引き起こすためです。このコマンドをresumeinput()と比較してください。
例
if (current.subnodes.length < maxcontent)
openinput(current);
openinput(current);
openoutput (obj object)
廃止、Object.output.open()を使用すること
説明
このコマンドは廃止されました。代わりにObject.output.open()を使用してください。
このコマンドは、以前にcloseoutput()コマンドでブロックされたオブジェクトの出力のブロックを解除します。退出を許可する前に、出力ポート自体と出力全般を開く必要があります。モデラーは、senddelayedmessage()コマンドによりトリガーされたOnMessageフィールドを除いて、いかなるフィールドでもこのコマンドを使用しないことをお勧めします。これは、ポートを開くコマンドは多くの場合、トランジションイベントで行うべきでない複数の他の動作を引き起こすためです。このコマンドをresumeoutput()と比較してください。
このコマンドは、以前にcloseoutput()コマンドでブロックされたオブジェクトの出力のブロックを解除します。退出を許可する前に、出力ポート自体と出力全般を開く必要があります。モデラーは、senddelayedmessage()コマンドによりトリガーされたOnMessageフィールドを除いて、いかなるフィールドでもこのコマンドを使用しないことをお勧めします。これは、ポートを開くコマンドは多くの場合、トランジションイベントで行うべきでない複数の他の動作を引き起こすためです。このコマンドをresumeoutput()と比較してください。
例
if (current.subnodes.length > mincontent)
openoutput(current);
openoutput(current);
or (num/node condition1, num/node condition2)
廃止、||オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに||オペレーターを使用してください。
例
outobject (obj object, num outputportnum)
廃止、Object.outObjects[]を使用すること
説明
例
parg ()
説明
このコマンドは廃止されました。
例
parg()
parnode (num index)
廃止、param()を使用すること
説明
このコマンドは廃止されました。代わりにparamを使用してください。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。nodefunctionに渡された、indexにより指定されたパラメータを、ノード(またはツリーノード)として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparval()およびparstr()で取得し、それぞれ数値と文字列にキャストすることもできます。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。nodefunctionに渡された、indexにより指定されたパラメータを、ノード(またはツリーノード)として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparval()およびparstr()で取得し、それぞれ数値と文字列にキャストすることもできます。
例
トリガー/フィールドが
nodefunction(thefuncnode, item)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたアイテムへのアクセスが、次のように取得されます。
treenode item = parnode(1);
nodefunction(thefuncnode, item)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたアイテムへのアクセスが、次のように取得されます。
treenode item = parnode(1);
parstr (num index)
廃止、param()を使用すること
説明
このコマンドは廃止されました。代わりにparamを使用してください。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。nodefunctionに渡された、indexにより指定されたパラメータを、文字列として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparam()コマンドで取得することもできます。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。nodefunctionに渡された、indexにより指定されたパラメータを、文字列として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparam()コマンドで取得することもできます。
例
トリガー/フィールドが
nodefunction(thefuncnode, passingstr)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたpassingstr文字列へのアクセスが、次のように取得されます。
string passedstr = parstr(1);
nodefunction(thefuncnode, passingstr)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたpassingstr文字列へのアクセスが、次のように取得されます。
string passedstr = parstr(1);
particleset ()
廃止、使用しないこと
説明
このコマンドは廃止されました。「particle」オブジェクトに値を設定するため使用されていましたが、このオブジェクトのサポートは終了しました。
例
parval (num index)
廃止、param()を使用すること
説明
このコマンドは廃止されました。代わりにparamを使用してください。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。indexにより指定されたnodefunctionに渡されたパラメータを、数値として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparnode()およびparstr()で取得し、それぞれツリーノードと文字列にキャストすることもできます。
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。indexにより指定されたnodefunctionに渡されたパラメータを、数値として返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。パラメータをparnode()およびparstr()で取得し、それぞれツリーノードと文字列にキャストすることもできます。
例
トリガー/フィールドが
nodefunction(thefuncnode, passingval)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたpassingvalへのアクセスが、次のように取得されます。
double passedval = parval(1);
nodefunction(thefuncnode, passingval)
で呼び出された場合、そのトリガー/フィールド内で、最初の追加パラメータとして渡されたpassingvalへのアクセスが、次のように取得されます。
double passedval = parval(1);
pc (num asciivalue)
廃止、print()を使用すること
説明
このコマンドは廃止されました。代わりにprint()コマンドを使用してください。
ASCII文字を出力コンソールに表示します。
ASCII文字を出力コンソールに表示します。
例
pd (num value)
廃止、print()を使用すること
説明
このコマンドは廃止されました。代わりにprint()コマンドを使用してください。
整数を出力コンソールに表示します。
整数を出力コンソールに表示します。
例
pf (num value)
廃止、print()を使用すること
説明
このコマンドは廃止されました。代わりにprint()コマンドを使用してください。
浮動小数点数を出力コンソールに表示します。
浮動小数点数を出力コンソールに表示します。
例
port <括弧なし>
説明
このコマンドは廃止されました。このコマンドは、今後setportコマンドとともに特殊コマンドとして使用してはいけません。代わりに、int変数タイプをポートとして宣言し、コード内で他の変数タイプと同様にポートを使用してください。
例
int port = param(3);
pd(port);
ポートをparam(3)に設定し、出力コンソールに値を表示します。
pd(port);
ポートをparam(3)に設定し、出力コンソールに値を表示します。
pow (num num1, num num2)
pr ()
廃止、print()を使用すること
説明
このコマンドは廃止されました。代わりにprint()コマンドを使用してください。
出力コンソールに改行を出力します。
出力コンソールに改行を出力します。
例
prev (obj object)
pt (str text)
廃止、print()を使用すること
説明
このコマンドは廃止されました。代わりにprint()コマンドを使用してください。出力コンソールにテキストを表示します。
例
query (str query[, node/num/str p1, node/num/str p2, ...])
radianstodegrees (num value)
rank (obj parent, num index)
rankobj (obj container, num rank)
reftable (str/num globaltable)
廃止、Table("GlobalTableName")を使用すること
説明
このコマンドは廃止されました。代わりにTableクラスを使用してください。
グローバルテーブルへの参照を取得します。
グローバルテーブルへの参照を取得します。
例
Table table = reftable("GlobalTable1")
relloc (obj object, obj containerobj, num coordinate)
廃止、Vec3.project()を使用すること
説明
例
double x = relloc(current,model(),1);
double y = relloc(current,model(),2);
double z = relloc(current,model(),3);
x、y、zに、currentオブジェクトのx、y、z位置を、モデル空間への相対位置として設定します。
double y = relloc(current,model(),2);
double z = relloc(current,model(),3);
x、y、zに、currentオブジェクトのx、y、z位置を、モデル空間への相対位置として設定します。
repeat (num nr, expression)
説明
指定された回数だけ式を実行します。式では「count」を使用して実行された繰り返し回数を取得できます(1から始まります)。
例
repeat(current.outObjects.length, current.outObjects[count].input.close);
この例は、currentの出力ポートに接続されているすべてのオブジェクトの入力を閉じます。
この例は、currentの出力ポートに接続されているすべてのオブジェクトの入力を閉じます。
reset ()
廃止、resetmodel()を使用すること
説明
このコマンドは廃止されました。代わりにresetmodel()を使用してください。
開発者向けです。このコマンドはモデルをリセットします。シミュレーションクロックは0に設定され、モデルのすべてのオブジェクトについてOnResetイベント関数が呼び出されます。OnResetイベントは一般に、ユーザーが定義したResetTrigger関数を呼び出します。モデルはリセット前にコンパイル済みの必要があります。通常は、reset()の代わりにresetmodel()コマンドを呼び出します。
開発者向けです。このコマンドはモデルをリセットします。シミュレーションクロックは0に設定され、モデルのすべてのオブジェクトについてOnResetイベント関数が呼び出されます。OnResetイベントは一般に、ユーザーが定義したResetTrigger関数を呼び出します。モデルはリセット前にコンパイル済みの必要があります。通常は、reset()の代わりにresetmodel()コマンドを呼び出します。
例
reset();
go();
モデルをリセットしてから実行します。
go();
モデルをリセットしてから実行します。
resumeinput (obj object)
resumeobject (obj object [, num id, num stateprofile ] )
resumeoutput (obj object)
richeditaddtext (obj richedit, str text, num protected (0/1))
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
richedittoken (obj richedit, num tokenindex)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
round (num value[, num precision])
savefpk (node servicepackhead)
廃止、ユーザーライブラリを使用すること
説明
このコマンドは廃止されました。代わりにユーザーライブラリを使用してください。
ノードをサービスパックファイル(.fpk)としてディスクに保存します。
ファイルの保存ダイアログボックスが表示され、ファイルのパスと名前を定義できます。サービスパックは、サブノードを持つノードです。最初のサブノードはトグルされたflexscriptで、文字列データとコードを含むと見なされます。サービスパックが[ファイル]|[サービスパックのインストール]を使用してロードされると、サービスパックの最初のサブノードが自動的に実行されます。このコードは通常、他のサブノードをMAINおよびVIEWツリーにコピーします。
ノードをサービスパックファイル(.fpk)としてディスクに保存します。
ファイルの保存ダイアログボックスが表示され、ファイルのパスと名前を定義できます。サービスパックは、サブノードを持つノードです。最初のサブノードはトグルされたflexscriptで、文字列データとコードを含むと見なされます。サービスパックが[ファイル]|[サービスパックのインストール]を使用してロードされると、サービスパックの最初のサブノードが自動的に実行されます。このコードは通常、他のサブノードをMAINおよびVIEWツリーにコピーします。
例
savefpk(so());
set (node thenode, num value)
setcenter (obj object, num x, num y, num z)
廃止、Object.setLocation()を使用すること
説明
例
setcolor (obj object, num red, num green, num blue)
setcurrent (thing)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
setitem (thing)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
setitemtype (obj object, num value)
廃止、ラベルを使用すること
説明
このコマンドは廃止されました。代わりにラベルを使用してください。
このコマンドは、オブジェクトのitemtype属性をvalueに設定します。オブジェクトにitemtype属性が存在しない場合、このコマンドは何もしません。itemtype属性は通常、同じクラスでタイプが異なるフローアイテムを区別するため使用されます。
このコマンドは、オブジェクトのitemtype属性をvalueに設定します。オブジェクトにitemtype属性が存在しない場合、このコマンドは何もしません。itemtype属性は通常、同じクラスでタイプが異なるフローアイテムを区別するため使用されます。
例
setitemtype(item,duniform(1,3));
itemで参照されるフローアイテムのitemtype属性を、1から3までのランダムな整数に設定します。
itemで参照されるフローアイテムのitemtype属性を、1から3までのランダムな整数に設定します。
setlabel (obj node, str/num label, num/str/node value)
廃止、treenode.LabelNameを使用すること
説明
例
setlabelnum (obj object, str/num label, num value)
廃止、treenode.LabelNameを使用すること
説明
例
setlabelstr (obj object, str/num label, str value)
廃止、treenode.LabelNameを使用すること
説明
例
setloc (obj object, num x, num y, num z[, num xFactor, num yFactor, num zFactor])
setname (obj object, str value)
setnodename (obj/node object, str value)
setnodenum (node thenode, num value)
setnodestr (node thenode, str value)
setobjectimageindex (obj object, num index)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
オブジェクトのベースに割り当てられているbmpまたはjpeg画像(2D形状およびベース画像)のインデックス番号を設定します。新しいインデックスを有効にするには、オブジェクトのimagebaseノードを削除するか、名前を変更する必要があるため、このコマンドはimagebaseノードの名前を「_imagebase」に変更します。インデックス番号は、現在インポートされているbmpまたはjpeg画像の有効なインデックス番号の必要があります。現在インポートされている画像を表示する、または別のbmpやjpeg画像をインポートするには、ツールボックスの[メディアをインポート]オプションを使用してください。
オブジェクトのベースに割り当てられているbmpまたはjpeg画像(2D形状およびベース画像)のインデックス番号を設定します。新しいインデックスを有効にするには、オブジェクトのimagebaseノードを削除するか、名前を変更する必要があるため、このコマンドはimagebaseノードの名前を「_imagebase」に変更します。インデックス番号は、現在インポートされているbmpまたはjpeg画像の有効なインデックス番号の必要があります。現在インポートされている画像を表示する、または別のbmpやjpeg画像をインポートするには、ツールボックスの[メディアをインポート]オプションを使用してください。
例
setobjectimageindex(item,gettextureindex("fs3d\\BBsphere.bmp"));
setport (thing)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
setquerynode (node queryNode)
setrank (obj/node object, num index)
setrot (obj object, num rx, num ry, num rz)
sets (node thenode, str value)
setsize (obj object, num sx, num sy, num sz)
setstate (obj object, num state [, num profilenr])
setstate_s (obj object, str statename)
settable (node table, num sx, num sy[, num type, num overwrite])
廃止、Tableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスを使用してください。
例
settableheader (string/num/node table, num row/col, num rowcolnr, string value)
廃止、Table.setColHeader()またはTable.setRowHeader()を使用すること
説明
例
settablenum (str/node/num table, num row, num col, num value)
廃止、Tableの[]オペレーターを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスの[]オペレーターを使用してください。
テーブルのセルの数値を設定します。
テーブルのセルの数値を設定します。
例
settablesize (str/num/node table, num rows, num cols [, num datatype, num overwrite y/n])
settablestr (str/node/num table, num row, num col, str value)
廃止、Tableの[]オペレーターを使用すること
説明
このコマンドは廃止されました。代わりにTableクラスの[]オペレーターを使用してください。
テーブルのセルのテキスト値を設定します。
テーブルのセルのテキスト値を設定します。
例
settrackedvariable (str/node trackedvar, num value[, num rate])
廃止、TrackedVariableクラスを使用すること
説明
このコマンドは廃止されました。代わりにTrackedVariableクラスを使用してください。
例
setundos (num maxundos)
廃止
説明
このコマンドは廃止されました。このコマンドを使用しない、より高速で軽量な取り消し機能の実装が開発されたため、このコマンドは現在では廃止されています。
許可される取り消しの最大数を設定します。マウスがクリックされるか、キーが押されるごとに、モデル全体のコピーが保存されます。setundosコマンドを使用して、取り消し用に記憶されるモデルのコピーの最大数を指定できます。このコマンドを使用するには、最初にメインツリーにundoという名前のノードを作成し、数値データを与える必要があります。
許可される取り消しの最大数を設定します。マウスがクリックされるか、キーが押されるごとに、モデル全体のコピーが保存されます。setundosコマンドを使用して、取り消し用に記憶されるモデルのコピーの最大数を指定できます。このコマンドを使用するには、最初にメインツリーにundoという名前のノードを作成し、数値データを与える必要があります。
例
setundos(2);
showgraphicinfo (num showhide, str filename)
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。
例
sin (num angle)
sorttable (str/node/num table, num column)
spaceglobal ()
廃止、drawtomodelscale()を使用すること
説明
このコマンドは廃止されました。代わりにdrawtomodelscale()を使用してください。
OpenGL空間をグローバルマトリクスに設定します。
OpenGL空間をグローバルマトリクスに設定します。
例
spaceglobal()
spaceobject ()
廃止、drawtoobjectscale()を使用すること
説明
このコマンドは廃止されました。使用してはいけません。代わりにdrawtoobjectscale()を使用してください。
例
spaceobject()
startanimation (obj object, num/str animation[, num speedtype, num speedvalue, num repeattype, num repeatvalue])
廃止、Animationクラスを使用すること
説明
このコマンドは廃止されました。代わりにAnimationクラスを使用してください。
objectのアニメーションを開始します。
objectのアニメーションを開始します。
例
startanimation(current, "Stand");
statisticaltime ()
廃止、Modelクラスを使用すること
説明
このコマンドは廃止されました。代わりにModel.statisticalTimeを使用してください。
実験でウォームアップ時間が経過した後、またはresetstats()が実行された後など、状態が最後にリセットされたときに相対的な現在のシミュレーション時間を返します。
実験でウォームアップ時間が経過した後、またはresetstats()が実行された後など、状態が最後にリセットされたときに相対的な現在のシミュレーション時間を返します。
例
item.TimeIn = statisticaltime();
itemで参照されるオブジェクトの「TimeIn」というラベルを、現在のシミュレーションクロック時間に設定します。
itemで参照されるオブジェクトの「TimeIn」というラベルを、現在のシミュレーションクロック時間に設定します。
stopanimation (obj object, num/str animation)
廃止、Animationクラスを使用すること
説明
このコマンドは廃止されました。代わりにAnimationクラスを使用してください。
オブジェクトのアニメーションを停止します。
オブジェクトのアニメーションを停止します。
例
stopanimation(current, "Walk");
stopinput (obj object)
stopobject (obj object, num state [, num id, num priority, num stateprofile] )
廃止、Object.stop()を使用すること
説明
このコマンドは廃止されました。代わりにObject.stop()を使用してください。
オブジェクトに対して、現在行っている動作を停止し、指定された状態に移行して(指定されているなら状態プロファイルの状態に)、resumeobject()が呼び出されるまで待つように通知します。stopobjectコマンドは累積されます。すなわち、同じオブジェクトに対してstopobjectが2回呼び出されると、そのオブジェクトはresumeobjectが同様に2回呼び出されるまで動作を再開しません。オブジェクトの停止は、停止されるオブジェクトのタイプによって異なります。
FixedResourcesの場合、一般にイベントが無期限に遅延され、入力と出力が停止され、オブジェクトへ、およびオブジェクトからのあらゆる動作は停止されます。このため、TaskExecutersがオブジェクトへのロードやオブジェクトからのアンロードを試みるには、オブジェクトの再開まで待つ必要があります。
TaskExecutersの場合、イベントは遅延されませんが、TaskExecuter用に優先度100,000のプリエンプトのタスクシーケンスが作成され、その中に1つのTE_STOPタスクが含まれます。
同じオブジェクトに複数の停止リクエストが存在する場合、それぞれの停止リクエストの状態は記憶されないことに注意してください。オブジェクトがエンティティAにより状態12での停止を要求され、その後でエンティティBにより状態14での停止を要求された場合、オブジェクトは状態14に移行し、状態12は記憶されません。エンティティBがエンティティAより前にオブジェクトを再開させても、オブジェクトはすべての停止リクエストが再開されるまで状態14に維持されます。
最後の2つのパラメータidとpriorityはオプションで、前の段落に記載された問題を修正するために最近追加されたものです。これらのパラメータが指定されると、要求された停止の回数を増やすだけでなく、停止リクエストのレコードが保存されます。idは停止リクエストのキーと同様に扱われます。priorityは、オブジェクトが停止リクエストを優先度付けするために使用されます。たとえば、スケジュールされた停止状態用の停止リクエストと、故障状態用の停止リクエストが同時に存在する場合、オブジェクトは理論的には同時に2つの状態に置かれるべきですが、FlexSimのオブジェクトは同時に1つの状態しかとれないため、優先度の値で判断され、優先度が最も高い停止リクエストの状態に移行します。
id値は、後でresumeobject()コマンドに追加されるid値と一致する必要があります。この値は、停止リクエストと、対応する再開リクエストを一致するために使用されます。たとえば、オブジェクトをスケジュールされた保守のため、id値1で停止した場合、スケジュールされた保守が完了したら、同じ1のid値でオブジェクトを再開する必要があります。
オブジェクトに対して、現在行っている動作を停止し、指定された状態に移行して(指定されているなら状態プロファイルの状態に)、resumeobject()が呼び出されるまで待つように通知します。stopobjectコマンドは累積されます。すなわち、同じオブジェクトに対してstopobjectが2回呼び出されると、そのオブジェクトはresumeobjectが同様に2回呼び出されるまで動作を再開しません。オブジェクトの停止は、停止されるオブジェクトのタイプによって異なります。
FixedResourcesの場合、一般にイベントが無期限に遅延され、入力と出力が停止され、オブジェクトへ、およびオブジェクトからのあらゆる動作は停止されます。このため、TaskExecutersがオブジェクトへのロードやオブジェクトからのアンロードを試みるには、オブジェクトの再開まで待つ必要があります。
TaskExecutersの場合、イベントは遅延されませんが、TaskExecuter用に優先度100,000のプリエンプトのタスクシーケンスが作成され、その中に1つのTE_STOPタスクが含まれます。
同じオブジェクトに複数の停止リクエストが存在する場合、それぞれの停止リクエストの状態は記憶されないことに注意してください。オブジェクトがエンティティAにより状態12での停止を要求され、その後でエンティティBにより状態14での停止を要求された場合、オブジェクトは状態14に移行し、状態12は記憶されません。エンティティBがエンティティAより前にオブジェクトを再開させても、オブジェクトはすべての停止リクエストが再開されるまで状態14に維持されます。
最後の2つのパラメータidとpriorityはオプションで、前の段落に記載された問題を修正するために最近追加されたものです。これらのパラメータが指定されると、要求された停止の回数を増やすだけでなく、停止リクエストのレコードが保存されます。idは停止リクエストのキーと同様に扱われます。priorityは、オブジェクトが停止リクエストを優先度付けするために使用されます。たとえば、スケジュールされた停止状態用の停止リクエストと、故障状態用の停止リクエストが同時に存在する場合、オブジェクトは理論的には同時に2つの状態に置かれるべきですが、FlexSimのオブジェクトは同時に1つの状態しかとれないため、優先度の値で判断され、優先度が最も高い停止リクエストの状態に移行します。
id値は、後でresumeobject()コマンドに追加されるid値と一致する必要があります。この値は、停止リクエストと、対応する再開リクエストを一致するために使用されます。たとえば、オブジェクトをスケジュールされた保守のため、id値1で停止した場合、スケジュールされた保守が完了したら、同じ1のid値でオブジェクトを再開する必要があります。
例
stopobject(current.centerObjects[1], STATE_BLOCKED);
stopoutput (obj object)
store ()
説明
このコマンドは廃止されました。このコマンドを使用しない、より高速で軽量な取り消し機能の実装が開発されたため、このコマンドは現在では廃止されています。
現在のモデルのアーカイブされたコピーを、メインツリーの取り消しフォルダに明示的に保存します。詳細については、undos()コマンドのドキュメントを参照してください。
現在のモデルのアーカイブされたコピーを、メインツリーの取り消しフォルダに明示的に保存します。詳細については、undos()コマンドのドキュメントを参照してください。
例
store();
stringcopy (str string, num start, num length)
stringlen (str string)
stringpart (str string, num start, num length)
stringreplace (str stringtosearch, str searchfor, str replacewith)
stringreturn (str returnstring, ptr callpoint)
説明
このコマンドは廃止されました。returnステートメントを使用して、C++のユーザーコマンドから簡単に文字列を返すことができます。
FlexSim 7.7より以前では、ユーザーコマンドのC++実装から文字列を返すために、このコマンドが使用されていました。このコマンドはC++でのみ必要でした。FlexScriptのユーザーコマンドでは、returnステートメントで簡単に文字列を返すことができます。
FlexSim 7.7より以前では、ユーザーコマンドのC++実装から文字列を返すために、このコマンドが使用されていました。このコマンドはC++でのみ必要でした。FlexScriptのユーザーコマンドでは、returnステートメントで簡単に文字列を返すことができます。
例
C++: stringreturn(result, callpoint); return 0;
stringsearch (str stringtosearch, str searchfor, int startindex[, int flags])
stringtonum (str string)
stringtopchar (str string)
廃止、apchar()を使用すること
説明
このコマンドは廃止されました。代わりにapchar()を使用してください。
このコマンドは、C++文字へのポインタとしして文字列を返します。char*のみを受け付ける一部のC++コマンド用に、stringタイプの変数をchar*タイプに変換するため使用されます。Flexscriptでは必要ありません。
このコマンドは、C++文字へのポインタとしして文字列を返します。char*のみを受け付ける一部のC++コマンド用に、stringタイプの変数をchar*タイプに変換するため使用されます。Flexscriptでは必要ありません。
例
setname(current,stringtopchar("ThisObjectName"));
currentで参照されるオブジェクトの名前を「ThisObjectName」に設定します。ここでstringtopchar()コマンドは必須ではありませんが、正当です。
currentで参照されるオブジェクトの名前を「ThisObjectName」に設定します。ここでstringtopchar()コマンドは必須ではありませんが、正当です。
strquote (str string)
廃止、\"を使用すること
説明
このコマンドは廃止されました。文字列に引用符を含めるには、代わりに\"を使用してください。
例
strquote("hello")
sub (num value1, num value2)
廃止、-オペレーターを使用すること
説明
このコマンドは廃止されました。代わりに-オペレーターを使用してください。
value1とvalue2の代わりにオペレーターを使用してください。数値演算式value1-value2の結果を返します。
value1とvalue2の代わりにオペレーターを使用してください。数値演算式value1-value2の結果を返します。
例
代わりにdoubleオペレーターを使用してください。 = sub(10,4);
swaptablecols (str/num/node table, num column, num column2)
swaptablerows (str/num/node table, num row, num row2)
switch_hidebase (obj object[, num off/on])
廃止、使用しないこと
説明
このコマンドは廃止されました。使用してはいけません。オブジェクトの「2D形状を表示」フラグを取得または設定します。値が1なら非表示、0なら表示、-1なら現在の値を取得します。オブジェクトの2D形状(ベース)は、平面ビューウィンドウに表示されます。ビューウィンドウにはhideallbasesという名前の属性もあり、ビュー内のすべてのオブジェクトについて2D形状(ベース)の表示をコントロールしていることに注意してください。
例
switch_hidebase(so(),1)
tan (num angle)
time ()
trackedvariable (str name)
廃止、追跡変数クラスを使用すること
説明
このコマンドは廃止されました。代わりにTrackedVariableクラスを使用してください。
例
transfernode (node movenode, node container)
travelto (obj object, obj spline, num x, num y, num z, num vmax, num acc, num dec)
廃止、キネマティクスを使用すること
説明
このコマンドは廃止されました。代わりにキネマティクスを使用してください。
オブジェクトの現在の移動パラメータを計算します。移動パスが計算されます。設定されると、このコマンドにより定義された移動パスに基づいてオブジェクトの位置が計算されます。この関数は、移動の終了時間を返します。この関数をスプラインと組み合わせて使用し、曲線の移動パスを作成できます。
オブジェクトの現在の移動パラメータを計算します。移動パスが計算されます。設定されると、このコマンドにより定義された移動パスに基づいてオブジェクトの位置が計算されます。この関数は、移動の終了時間を返します。この関数をスプラインと組み合わせて使用し、曲線の移動パスを作成できます。
例
travelto(traveler,NULL,100,100,0,5,1,6)
traveltoupdate (obj object [, obj spline])
廃止、キネマティクスを使用すること
説明
このコマンドは廃止されました。代わりにキネマティクスを使用してください。
現在の移動パラメータに基づいてオブジェクトの位置を更新します。オブジェクトに対して実行されたtravelto()コマンドで計算された時間および移動パスのパラメータに基づいて、オブジェクトの位置を明示的に設定します。必要なら、パスのジオメトリとしてスプラインを使用します。
現在の移動パラメータに基づいてオブジェクトの位置を更新します。オブジェクトに対して実行されたtravelto()コマンドで計算された時間および移動パスのパラメータに基づいて、オブジェクトの位置を明示的に設定します。必要なら、パスのジオメトリとしてスプラインを使用します。
例
traveltoupdate(current)
以前のtraveto()コマンドで設定された移動パラメータに基づいて、currentオブジェクトの位置を更新します。このコマンドは通常、[カスタム描画コード]フィールドから実行されます。
以前のtraveto()コマンドで設定された移動パラメータに基づいて、currentオブジェクトの位置を更新します。このコマンドは通常、[カスタム描画コード]フィールドから実行されます。
undos (num off/on)
説明
このコマンドは廃止されました。このコマンドを使用しない、より高速で軽量な取り消し機能の実装が開発されたため、このコマンドは現在では廃止されています。
このコマンドは、マウスがクリック、またはキーが押されるごとにモデルのコピーを自動的に保存するか(1)、しないか(0)を設定するため使用されます。setundosコマンドを使用して、取り消し用に記憶されるモデルのコピーの最大数を指定できます。このコマンドが正しく機能するには、最初にメインツリーにundoという名前のノードを作成し、数値データを与える必要があります。
このコマンドは、マウスがクリック、またはキーが押されるごとにモデルのコピーを自動的に保存するか(1)、しないか(0)を設定するため使用されます。setundosコマンドを使用して、取り消し用に記憶されるモデルのコピーの最大数を指定できます。このコマンドが正しく機能するには、最初にメインツリーにundoという名前のノードを作成し、数値データを与える必要があります。
例
undos(1);
updateanimation (obj object [, num updatetime, num animationnr])
廃止、Animationクラスを使用すること
説明
このコマンドは廃止されました。代わりにAnimationクラスを使用してください。
オブジェクトのアニメーションを更新します。
オブジェクトのアニメーションを更新します。
例
updateanimation(current);
userfunction_n (obj object, num index [, num param_a,...])
廃止、nodefunction()を使用すること
説明
このコマンドは廃止されました。nodefunction()はどのノードにも使用できるため、こちらを使用してください。
オブジェクトのuserfunctionsグループにある、指定されたランクのindexを持つノードと関連付けられているコードを実行します。呼び出された関数ノードの中でparam()を使用し、関数に渡された引数を取得してください。
オブジェクトのuserfunctionsグループにある、指定されたランクのindexを持つノードと関連付けられているコードを実行します。呼び出された関数ノードの中でparam()を使用し、関数に渡された引数を取得してください。
例
userfunction_s(current,4,1,2,3)
currentオブジェクトのuserfunctionsグループ内で4番目にランクされているノードと関連付けられているコードを実行します。
currentオブジェクトのuserfunctionsグループ内で4番目にランクされているノードと関連付けられているコードを実行します。
userfunction_s (obj object, str name [, num param_a,...])
廃止、nodefunction()を使用すること
説明
このコマンドは廃止されました。nodefunction()はどのノードにも使用できるため、こちらを使用してください。
オブジェクトのuserfunctionsグループにある、指定された名前を持つノードと関連付けられているコードを実行します。呼び出された関数ノードの中でparam()を使用し、関数に渡された引数を取得してください。
オブジェクトのuserfunctionsグループにある、指定された名前を持つノードと関連付けられているコードを実行します。呼び出された関数ノードの中でparam()を使用し、関数に渡された引数を取得してください。
例
userfunction_s(current,"myfunc",1,2,3)
currentオブジェクトのuserfunctionsグループ内の、「myfunc」という名前のノードと関連付けられているコードを実行します。
currentオブジェクトのuserfunctionsグループ内の、「myfunc」という名前のノードと関連付けられているコードを実行します。
var (obj object, num index)
廃止、getvarnode()を使用すること
説明
このコマンドは廃止されました。代わりにgetvarnode()を使用してください。
「variables」内のオブジェクトのノードをインデックスで取得します。
「variables」内のオブジェクトのノードをインデックスで取得します。
例
var(so(),1)
var_s (obj object, str name)
廃止、getvarnode()を使用すること
説明
このコマンドは廃止されました。代わりにgetvarnode()を使用してください。
「variables」内のオブジェクトのノードを名前で取得します。
「variables」内のオブジェクトのノードを名前で取得します。
例
var_s(current,"myatt")
vectorprojectx (obj projectfrom, num fromx, num fromy, num fromz, obj projectonto)
vectorprojecty (obj projectfrom, num fromx, num fromy, num fromz, obj projectonto)
vectorprojectz (obj projectfrom, num fromx, num fromy, num fromz, obj projectonto)
xcenter (obj object)
廃止、Object.getLocation()を使用すること
説明
例
xloc (obj object)
廃止、Object.locationまたはObject.getLocation()を使用すること
説明
例
xrot (obj object)
廃止、Object.rotationまたはObject.setRotation()を使用すること
説明
例
xsize (obj object)
ycenter (obj object)
廃止、Object.getLocation()を使用すること
説明
例
yloc (obj object)
廃止、Object.locationまたはObject.getLocation()を使用すること
説明
例
yrot (obj object)
ysize (obj object)
zcenter (obj object)
廃止、Object.getLocation()を使用すること
説明
例
zloc (obj object)
廃止、Object.locationまたはObject.getLocation()を使用すること
説明
例
zrot (obj object)
zsize (obj object)
開発
高レベルの開発コマンドで、一般にエンドユーザー向けではありません。
addcommand (obj codenode, str commandname, str description, str parameters, str example [, str cppprefix, str shortdescription])
説明
開発者向けです。現在利用可能なコマンドのリストにFlexscriptコマンドを追加します。新しいコマンドは、次にコンパイルを行うときまで利用可能です。エンドユーザーが独自のコマンドを作成するには、[ツール]|[ユーザーコマンド]メニューを使用できます。
例
addcommand(...)
backupfile (str filepath)
説明
開発者向けです。指定されたファイルの名前に!を追加し、ファイルをバックアップします。ファイルのコピーは行われないことに注意してください。ファイルを上書きする前に使用します。
例
backupfile(modeldir() + "mydocument.htm");
buildall ()
説明
開発者向けです。このコマンドは、Flexscriptノードとして割り当てられているツリー内のすべてのノードについて、Flexscriptツリーを構築します。Flexscriptノードを実行する前に、Flexscriptツリーを作成する必要があります。このオプションは、メインメニューの[構築]->[すべてのFlexScriptを構築]で使用できます。モデルのどこかにFlexscriptが記述されている場合、そのモデルを実行する前にこの操作を行う必要があります。また、GUIに変更を加えた後もこの操作を行います。
例
buildall();
ツリー内のすべてのFlexscriptノードにFlexscriptツリーを構築します。
ツリー内のすべてのFlexscriptノードにFlexscriptツリーを構築します。
buildnodeflexscript (node codenode)
説明
開発者向けです。このコマンドは、ノードとして指定されたノードがFlexscriptノードとして割り当てられているなら、そのノード用のFlexscriptツリーを構築します。Flexscriptノードを実行する前に、Flexscriptツリーを作成する必要があります。
例
buildnodeflexscript(Table("mytable").cell(1,2));
「mytable」という名前のGlobalTableの行1、列2にあるノードがFlexscriptノードなら、そのノード用のFlexscriptツリーを構築します。
「mytable」という名前のGlobalTableの行1、列2にあるノードがFlexscriptノードなら、そのノード用のFlexscriptツリーを構築します。
changedisplay (num width, num height, num depth, num fullscreen, num test)
解像度を変更する
説明
解像度を変更します。
例
changedisplay(1024,768,0,0,0)
cleannodeflexscript (node startnode)
説明
開発者向けです。このコマンドは、指定されたノードから始めて、Flexscriptツリーを再帰的に削除します。
例
cleannodeflexscript(model());
モデル内のすべてのFlexscriptノードを削除します。
モデル内のすべてのFlexscriptノードを削除します。
cmdcompile ()
説明
開発者向けです。
プロジェクトをコンパイルします。
プロジェクトをコンパイルします。
例
cmdcompile()
cmddelete (node thenode)
説明
開発者向けです。destroyobject()を使用してください。
thenodeを削除します。
thenodeを削除します。
例
cmddelete(model().subnodes[4]))
cmdexit ()
説明
開発者向けです。
FlexSimを閉じます。
FlexSimを閉じます。
例
cmdexit()
cmdloadbyextension (str filename, num silent)
説明
開発者向けです。
名前と拡張子により指定されるファイルをロードします。次のファイルが認識されます:プロジェクト(fsp)、セッション(fss)、モデル(fsm)、ビューレイアウト(fsv)。silentが0なら、ユーザーは開くファイルが正しいことを確認するよう求められます。
名前と拡張子により指定されるファイルをロードします。次のファイルが認識されます:プロジェクト(fsp)、セッション(fss)、モデル(fsm)、ビューレイアウト(fsv)。silentが0なら、ユーザーは開くファイルが正しいことを確認するよう求められます。
例
cmdloadbyextension("c:/mysession.fss",0)
cmdloadsession (str filename)
説明
開発者向けです。
名前で指定されたセッションをロードします。
名前で指定されたセッションをロードします。
例
cmdloadsession("c:/mysession.fss")
cmdloadtree (obj desttree, str filename [, num nobuild])
説明
開発者向けです。
ファイルパスで指定されたツリーをdesttreeにロードします。デフォルトでは、ロード後にすべてのflexscriptが構築されます。nobuildが1なら、flexscriptは構築されません。flexscriptとして切り替えられるスクリプトノードからこのコマンドを実行する場合、nobuildに1を設定します。これを行わない場合、スクリプトは正常に終了しません。
ファイルパスで指定されたツリーをdesttreeにロードします。デフォルトでは、ロード後にすべてのflexscriptが構築されます。nobuildが1なら、flexscriptは構築されません。flexscriptとして切り替えられるスクリプトノードからこのコマンドを実行する場合、nobuildに1を設定します。これを行わない場合、スクリプトは正常に終了しません。
例
cmdloadtree(node("MAIN:/project/model/2"),"c:/mytree.t"))
cmdnew ()
説明
開発者向けです。
新しいモデルを開始します。このコマンドは、モデルのすべてのオブジェクトを削除し、モデルの内容をクリアします。
新しいモデルを開始します。このコマンドは、モデルのすべてのオブジェクトを削除し、モデルの内容をクリアします。
例
cmdnew()
cmdopen ()
説明
開発者向けです。
新しいモデルを開きます。このコマンドにより[モデルを開く]ダイアログボックスが表示され、開くモデルファイルを選択できます。
新しいモデルを開きます。このコマンドにより[モデルを開く]ダイアログボックスが表示され、開くモデルファイルを選択できます。
例
cmdopen()
cmdsaveas ()
説明
開発者向けです。
モデルを保存します。このコマンドにより[名前を付けてモデルを保存]ダイアログボックスが表示され、保存するモデルのファイル名を指定できます。
モデルを保存します。このコマンドにより[名前を付けてモデルを保存]ダイアログボックスが表示され、保存するモデルのファイル名を指定できます。
例
cmdsaveas()
cmdsavesession (str filename)
説明
開発者向けです。
名前を指定してセッションを保存します。
名前を指定してセッションを保存します。
例
cmdsavesession("c:/mysession.fss")
cmdsavetree (obj tree, str filename)
名前を指定してツリーを保存する
説明
名前を指定してツリーを保存します。
例
cmdsavetree(node("MAIN:/project/library/1"),"c:\\mytree.t"))
consoleexecutefs (HWND input, HWND output)
説明
開発者向けです。
コンソールコードをFlexscriptとして実行します。
コンソールコードをFlexscriptとして実行します。
例
copyattributes (obj destination, obj source, num mask)
説明
開発者向けです。オブジェクトから別のオブジェクトに属性をコピーします。maskパラメータを使用して、特定のグループを有効にできます(最下位ビットから)。
ATTCOPY_ALL
ATTCOPY_SPATIAL
ATTCOPY_OFFSETS
ATTCOPY_VISUAL
ATTCOPY_MEDIA ATTCOPY_LABELS
ATTCOPY_VARIABLES
ATTCOPY_DESCRIPTIVE
ATTCOPY_TABLES
ORオペレーター(|)を使用すると、これらの値をmaskパラメータの1つの値として組み合わせできます。
ATTCOPY_ALL
ATTCOPY_SPATIAL
ATTCOPY_OFFSETS
ATTCOPY_VISUAL
ATTCOPY_MEDIA ATTCOPY_LABELS
ATTCOPY_VARIABLES
ATTCOPY_DESCRIPTIVE
ATTCOPY_TABLES
ORオペレーター(|)を使用すると、これらの値をmaskパラメータの1つの値として組み合わせできます。
例
copyattributes(library().subnodes[1],model().subnodes[1],ATTCOPY_SPATIAL | ATTCOPY_VISUAL)
copycolor (obj highlightedobj)
説明
開発者向けです。強調表示されたオブジェクトの色を、選択したオブジェクトすべてにコピーします。
例
copycolor(current)
copylabel (obj highlightedobject, str/obj labelnamenode)
説明
開発者向けです。パラメータ2で指定された名前、またはパラメータ2のノードの文字列データに保存されている名前のラベルを、パラメータ1のオブジェクトから、モデルで選択されたすべてのオブジェクトにコピーします。
例
copylabel(selectedobject(ownerview(c)), c.find(">labelname"))
copylabels (obj highlightedobj[, num mode])
説明
開発者向けです。パラメータ1のオブジェクトから、すべてのラベルを、モデルで選択されているすべてのオブジェクトにコピーします。デフォルトでは既存のラベルがすべてクリアされ、パラメータ1のオブジェクトのラベルで置き換えられます。modeが1なら、既存のラベルと同じ名前のラベルがコピーされた場合、既存のラベルが上書きされますが、それ以外の場合は変更されません。modeが2なら、選択されたオブジェクトに存在しないラベルのみがコピーされます。
例
copylabels(selectedobject(ownerview(c)), c.find(">labelname"))
copyvariable (obj fromobject, obj variablenamenode)
説明
開発者向けです。パラメータ2で指定されたノードに保持されている名前の変数を、パラメータ1のオブジェクトから、モデルで選択されているすべてのオブジェクトにコピーします。
例
copyvariable(selectedobject(ownerview(c)), c.find(">variablename"))
copyvariables (obj fromobject)
説明
開発者向けです。パラメータ1のオブジェクトから、すべての変数を、モデルで選択されているすべてのオブジェクトにコピーします。
例
copyvariables(selectedobject(ownerview(c)))
copyvisuals (obj highlightedobj [, num copyshapefactorsalso])
説明
開発者向けです。パラメータ1のオブジェクトから、すべてのビジュアルを、モデルで選択されているすべてのオブジェクトにコピーします。
例
copyvisuals(selectedobject(ownerview(c)),1)
daemonstate (num thing)
説明
開発者向けです。
次の状態を返します。
1 - クロック
2 - フライスルー
3 - ティッカー
次の状態を返します。
1 - クロック
2 - フライスルー
3 - ティッカー
例
daemonstate(1)
documentusercommands ()
説明
開発者向けです。現在のモデルのコマンドドキュメントにアクセスし、ユーザーコマンドがコマンドのドキュメントに含まれるよう、usercommands.xmlという名前のファイルを更新します。
例
documentusercommands();
excelupdatepreferences ()
システム使用のみ
説明
システム使用のみ - ユーザー設定と一致するよう、グローバル変数を更新します。startupRT.txt、およびExcelユーザー設定GUIのOnSelectで呼び出されます。
例
excelupdatepreferences()
fgldebuglevel (num level [0-3])
説明
開発者向けです。OpenGLのデバッグレベルを設定します。数値が大きいほどシステムが精密に調査され、多くの報告が行われます。0は調査なし、3は最大の精査です。
例
fgldebuglevel(3)
fileisreadonly (str filename)
説明
開発者向けです(Dynamo)。指定されたファイルのPROPERTY_COMMENTSから、「READONLY」という文字列を探します。
例
fileisreadonly(pdir() + "\\flexsim.exe")
fillwithatts (obj object, num attgroup)
説明
開発者向けです。属性グループからの属性をobjectに入力します。
例
fillwithatts(so(),1)
fscheckall (node startingnode)
説明
開発者向けです。このコマンドは、指定されたstartingnodeより下(それ自体も含む)にあるすべてのflexscriptノードのエラーをチェックし、最低1つのエラーが見つかればコンパイラーコンソールに結果を出力します。
例
fscheckall(main());
function_n (obj object, num index [, num param_a,...])
説明
開発者向けです。指定されたイベントコードを持つオブジェクトのeventfunctionsグループにあるノードと関連付けられているコードを実行します。イベントコードはeventfunctionsグループのノードのランクではなく、次に示す定義済みFlexSimイベントのいずれかに対応します:
OnReset 1
OnMessage 2
OnEvent 3
OnDraw 4
OnInopen 5
OnOutopen 6
OnReceive 7
OnSend 8
OnEntering 9
OnExiting 10
OnCompile 11
OnCreate 12
OnDestroy 13
OnLoad 14
OnCollision 15
OnClick 16
OnRunend 17
OnRunstart 18
OnInterrupted 19
OnCaptured 20
OnListen 21
OnPredraw 22
OnDrawplanar 23
OnPredrawplanar 24
OnPreListen 25
OnReset 1
OnMessage 2
OnEvent 3
OnDraw 4
OnInopen 5
OnOutopen 6
OnReceive 7
OnSend 8
OnEntering 9
OnExiting 10
OnCompile 11
OnCreate 12
OnDestroy 13
OnLoad 14
OnCollision 15
OnClick 16
OnRunend 17
OnRunstart 18
OnInterrupted 19
OnCaptured 20
OnListen 21
OnPredraw 22
OnDrawplanar 23
OnPredrawplanar 24
OnPreListen 25
例
function_n(current,1,1,2,3)
currentオブジェクトに定義されているOnResetイベント関数を実行します。
currentオブジェクトに定義されているOnResetイベント関数を実行します。
function_s (obj object, str name [, num param_a,...])
説明
開発者向けです。指定された名前を持つオブジェクトのeventfunctionsグループにあるノードと関連付けられているコードを実行します。FlexSimで定義済みのシステムレベルイベントのリストについては、function_n()コマンドのドキュメントを参照してください。
例
function_s(current,"OnReset",1,2,3)
currentオブジェクトに定義されているOnResetイベント関数を実行します。
currentオブジェクトに定義されているOnResetイベント関数を実行します。
getapplicationtitle ()
説明
開発者向けです。現在のアプリケーションのタイトルを文字列として返します。
例
msg(getapplicationtitle(),"Hello world.");
getnextparametersobject (obj startobject, str guifocus, num doguifocusclass, num searchforward)
説明
開発者向けです。パラメータウィンドウで、[次へ]ボタンが押されたとき、次のオブジェクトにアクセスするため使用されます。
例
ビューツリーのオブジェクトパラメータプロパティのウィンドウを参照します。
getproperty (str filename, num property)
説明
開発者向けです。指定されたファイルの、指定されたプロパティの値を取得します。
例
getproperty(modeldir() + "MyModel.fsm",1);
gettreedrawposition (node destnode, node roottree)
説明
開発者向けです。
例
groupconnectfrom (obj object, str character)
説明
開発者向けです。param(1)で渡されたオブジェクトを、param(2)で渡された文字を使用して、モデル内で選択されているすべてのオブジェクトと接続します。
一般にGUIで使用されます。
一般にGUIで使用されます。
例
groupconnectfrom(selectedobject(ownerview(c)),"A");
groupconnectto (obj object, str character)
説明
開発者向けです。モデル内で選択されているすべてのオブジェクトを、param(2)で渡された文字を使用して、param(1)で渡されたオブジェクトと接続します。
一般にGUIで使用されます。
一般にGUIで使用されます。
例
groupconnectto(selectedobject(ownerview(c)),"A");
groupcopyconnections (obj object)
説明
開発者向けです。param(1)で渡されたオブジェクトの接続を、モデル内で選択されているすべてのオブジェクトにコピーします。
一般にGUIで使用されます。
一般にGUIで使用されます。
例
groupcopyconnections(selectedobject(ownerview(c)));
help ()
説明
開発者向けです。ヘルプシステムのウィンドウを表示します。
例
help()
howmanyattributes ()
説明
開発者向けです。属性の数を返します。
例
howmanyattributes()
howmanycommands ()
説明
開発者向けです。コマンドの数を返します。
例
howmanycommands()
license ()
現在のライセンスタイプを取得する
説明
現在のライセンスタイプを取得します。
例
licenseactivation (num operation[, str buffer, var p1, node callback])
説明
開発者向けです。各種のライセンス操作を行います。
例
licenseactivation(LA_SET_ACTIVATION_SERVER_PARAMS,"@localhost",0);
maintenance (num command[, num state, str strparam])
説明
開発者向けです。保守スイッチを設定します。
最初のパラメータはオペレーションを割り当てます。2番目のパラメータは、設定する状態を割り当てます。
保守スイッチには次のものがあります。
0. このリストを出力する
1. デッドリンク
2. 属性のバインド方法(0=名前、1=インデックス、2=ブートストラップ)
3. numberprecision
4. バインディングレポートの表示
5. usercollisions
6. post-onsend
7. loadsavemode
8. disablefscheck
9. disablefspreprocess
10. splinetension
11. streamalizer
12. 拡張ドキュメントをただちにロード
13. 実験終了時にレポートを保存
14. オブジェクトライブラリのコンパイルを抑制
15. グローバルコンパイルを抑制
16. ランタイム情報の設定
17. ランタイム情報の取得
18. c++関数のバインド
19. c++関数の自動再バインドのオン/オフ
20. プレゼンテーションモードの取得
21. メインメニューの更新
22. optquestが有効か
23. flypathsの単位(秒)
24. chachedポートのオン/オフ
25. リセット時バインドのオン/オフ
26. カテゴリ名の設定(ユーザーコマンドグループは22、他のものは23、24以降は利用可能)
27. オブジェクトのsizermode 0、デフォルトは1。3軸
28. 非表示ノードをツリーに表示
29. 3dカーソルの非表示
30. simclock再描画の抑制
31. パーサー2の使用
32. グリッド描画の設定:ビット単位フィールド:0x1-グリッドを自動展開、0x2-グリッドの軸を表示、0x4-グリッドの原点を表示
1000. DDE
最初のパラメータはオペレーションを割り当てます。2番目のパラメータは、設定する状態を割り当てます。
保守スイッチには次のものがあります。
0. このリストを出力する
1. デッドリンク
2. 属性のバインド方法(0=名前、1=インデックス、2=ブートストラップ)
3. numberprecision
4. バインディングレポートの表示
5. usercollisions
6. post-onsend
7. loadsavemode
8. disablefscheck
9. disablefspreprocess
10. splinetension
11. streamalizer
12. 拡張ドキュメントをただちにロード
13. 実験終了時にレポートを保存
14. オブジェクトライブラリのコンパイルを抑制
15. グローバルコンパイルを抑制
16. ランタイム情報の設定
17. ランタイム情報の取得
18. c++関数のバインド
19. c++関数の自動再バインドのオン/オフ
20. プレゼンテーションモードの取得
21. メインメニューの更新
22. optquestが有効か
23. flypathsの単位(秒)
24. chachedポートのオン/オフ
25. リセット時バインドのオン/オフ
26. カテゴリ名の設定(ユーザーコマンドグループは22、他のものは23、24以降は利用可能)
27. オブジェクトのsizermode 0、デフォルトは1。3軸
28. 非表示ノードをツリーに表示
29. 3dカーソルの非表示
30. simclock再描画の抑制
31. パーサー2の使用
32. グリッド描画の設定:ビット単位フィールド:0x1-グリッドを自動展開、0x2-グリッドの軸を表示、0x4-グリッドの原点を表示
1000. DDE
例
maintenance(0)
modeleditmode (num/str mode)
説明
開発者向けです。現在のモデル編集モードを設定します。現在のモードは-1で照会できます。
例
modeleditmode("AConnect");
optquest (num command[, num action, num/str p1, num/str p2, num p3, num p4, num p5, num p6])
説明
開発者向けです。この単一のコマンドは、OptQuest DLLに定義されているすべての関数を呼び出します。
例
optquest(...)
postclosewindowmessage (obj view)
ウィンドウを閉じるWindowsメッセージをポストする
説明
ウィンドウを閉じるメッセージをWindowsメッセージキューにポストします。これにより、ウィンドウが実際に閉じる前にスクリプトコードを完了できます。
例
postclosewindowmessage(ownerview(c));
postmovewindowupdate (obj view)
説明
開発者向けです。使用してはいけません。
例
postwindowmessage (HWND window, num msg[, num/str/node wParam, num/str/node lParam])
説明
開発者向けです。メッセージをウィンドウにポストし、Windows APIのPostMessage()コマンドに直接アクセスします。ウィンドウハンドルにアクセスするには、windowfromnode()またはgetviewhwnd()を使用してください。詳細については、Windows APIのドキュメントを参照してください。[out]パラメータとしてlParamまたはwParamを使用するメッセージ、または構造体へのポインターを渡すメッセージは使用できないことに注意してください。lParamまたはwParamに文字列を渡すことが可能ですが、これらを[out]パラメータには使用できません。FlexSimのflexscriptマクロには、可能なすべてのWM_メッセージが含まれているわけではないため、flexscriptでこれらのメッセージを使用するには、Windowsのヘッダーファイルでその定義を見つけ、flexscriptコードに定義を追加する必要があります。
例
postwindowmessage(windowfromnode(view), WM_COPY, 0,0);
rebindobjectattributes (node thenode)
オブジェクトの属性を再バインドする
説明
与えられたノードのオブジェクト属性を再バインドします。オブジェクトの属性を削除または追加するとき、オブジェクトの属性キャッシュはその変更をすぐには反映しないため、rebindobjectattributesを呼び出してオブジェクトの属性キャッシュを更新できます。これは、オブジェクトを右クリックして[編集]|[オブジェクトの属性を再バインドする]を選択するのと同じです。
例
rebindobjectattributes(c)
recover (num phase)
復旧ファイルをロードする
説明
復旧ファイルをロードします。フェーズは1または2です。
例
recover(1)
refreshcommandlist ()
説明
開発者向けです。コマンドリストを更新します。
例
refreshcommandlist()
refreshglobalvariables ()
説明
開発者向けです。すべてのグローバル変数を初期値に更新します。
例
refreshglobalvariables()
refreshmodelcommands ()
説明
システムコマンド。使用してはいけません。
例
runexpertfit ()
説明
開発者向けです。ライセンスが存在すれば、エキスパートフィットプログラムを自動的に開始します。
例
runexpertfit()
sendwindowmessage (HWND window, num msg[, num/str/node wParam, num/str/node lParam])
説明
開発者向けです。Windows APIのSendMessage() コマンドに直接アクセスし、メッセージをウィンドウに送信します。ウィンドウハンドルにアクセスするには、windowfromnode()またはgetviewhwnd()を使用してください。詳細については、Windows APIのドキュメントを参照してください。[out]パラメータとしてlParamまたはwParamを使用するメッセージ、または構造体へのポインターを渡すメッセージは使用できないことに注意してください。lParamまたはwParamに文字列を渡すことが可能ですが、これらを[out]パラメータには使用できません。FlexSimのflexscriptマクロには、可能なすべてのWM_メッセージが含まれているわけではないため、flexscriptでこれらのメッセージを使用するには、Windowsのヘッダーファイルでその定義を見つけ、flexscriptコードに定義を追加する必要があります。
例
sendwindowmessage(windowfromnode(view), WM_COPY, 0,0);
setapplicationtitle (str title)
説明
開発者向けです。現在のアプリケーションのタイトルを設定します。
例
setapplicationtitle("Custom Application Title");
setmessageloopsleep (num interval, num sleeptime)
説明
開発者向けです。メッセージループの各サイクルについてスリープ時間を設定し、cpu負荷を減らします。この値が大きいとFlexSimがユーザー入力に応答しなくなる可能性があるため、使用には注意してください。intervalで指定されたミリ秒ごとに、FlexSimはsleeptimeで指定されたミリ秒だけ一時停止します。このコマンドは、過剰なcpu使用によって過熱する傾向がある、一部のラップトップで役立つことがあります。
例
setmessageloopsleep(1)
setproperty (str filename, num property, str newvalue)
説明
開発者向けです。指定されたファイルの、指定されたプロパティの値をnewvalueに設定します。
例
setproperty(modeldir() + "MyModel.fsm",1,"Custom Title");
setticker (node thenode[, num tickspersecond])
説明
開発者向けです。ティッカースクリプトノードを設定します。tickspersecondが指定された場合、コードは1秒ごとにその回数だけ実行されます。指定されない場合、ノードに関連付けられているコードはWindowsのイベントループの繰り返しごとに実行されます。ノードはFlexScriptまたはC++で切り替える必要があります。ティッカーノードの実行に関連してモデルイベントが作成されることはありません。ティッカー実行をオフにするには、setticker(0)を使用します。
例
setticker(so())
statsenablemask (num mask)
説明
開発者向けです。統計収集の要素を有効または無効にします。32ビットのイネーブルマスクとして、フラグの合計を設定します。ビット:0 = 状態、1 = フロー、2 = ポート内部。
例
statsenablemask(add(1,2))
stick (num stickno, num command [, HWND/num win, var/num p])
説明
開発者向けです。このコマンドは、ジョイスティックやコントローラーの状態を照会するか、機能を設定します。
sticknoは、照会するジョイスティックやゲームパッドのidを定義します。0から32までの数値です。通常は、コンピュータに接続されているジョイスティックは1つだけなので、sticknoの値には1を使用します。ゲームパッドを使用する場合、sticknoに2を使用することが必要な場合もあります。Xboxコントローラーの場合、sticknoの値は0から3までです。VRコントローラーの場合、sticknoは0または1です。Oculusタッチコントローラーの場合、sticknoの0は左手、1は右手です。sticknoに-1を使用すると、接続されているVRヘッドセットのステータス、位置、回転を取得できます。
commandは、このコマンドで実行する動作を定義します。次のマクロのいずれかを使用します。
STICK_JOY_STATUS - ジョイスティックの接続性を照会します。ジョイスティックが正しく接続されていれば、このコマンドは0を返します。戻り値が0以外の場合、ジョイスティックの接続性に何らかのエラーがあり、どのようなエラーなのかをシステムコンソールで確認できます。次のエラーが発生する可能性があります。
MMSYSERR_NODRIVER - ジョイスティックのドライバーが存在しません。
MMSYSERR_INVALPARAM - ジョイスティックのIDが無効か、hwndがNULLです。
JOYERR_NOCANDO - 必要なサービス(Windowsタイマーなど)が使用できないため、ジョイスティックの入力をキャプチャーできません。
JOYERR_UNPLUGGED - 指定されたジョイスティックはシステムに接続されていません。
JOYERR_PARMS - ジョイスティックのIDが無効か、hwndがNULLです。
STICK_JOY_XPOS - ジョイスティックの現在のX座標。0から65535までの数値です。0はジョイスティックが左へいっぱいまで押されていることを、65535は右へいっぱいまで押されていることを、32768は正確に中央の位置にあることを示します。ゲームパッドを使用している場合、左側のジョイスティックのx位置です。
STICK_JOY_YPOS - ジョイスティックの現在のY座標。この値も、0から65535までの数値です。0は上方向、65535は下方向を意味します。ゲームパッドを使用している場合、ゲームパッドの左側にあるジョイスティックの位置です。
STICK_JOY_ZPOS - ジョイスティックの現在のZ座標。ジョイスティックを使用している場合、これは通常、ジョイスティックのスロットルの現在の設定です。この値も、0から65535までの数値です。ゲームパッドを使用している場合、右側のジョイスティックのy位置を表します。
STICK_JOY_BUTTONS - ジョイスティックの32のボタンの現在の状態。ビット単位の整数で、各ビットは与えられたボタンの現在の状態を表します。ジョイスティックの場合、メインのトリガーボタンは通常0x00000001ビット、スティックの他のボタンは0x00000002および0x00000004、ジョイスティックのベースにあるボタンはより上位のビットで表されます。ジョイスティックごとに多少異なるので、自分でテストすることが必要です。
STICK_JOY_SET_CAPTURE - このコマンドは、ジョイスティックのキャプチャーを、指定したFlexSimウィンドウに設定します。このコマンドにはwinとpのパラメータを渡す必要があります。このコマンドを実行すると、ビューのOnStick属性にジョイスティックのメッセージが送信されます。たとえば、正投影ビューでジョイスティックのイベントをリッスンする場合、このコマンドを呼び出し、正投影ビューのHWNDハンドル(windowfromnode()を使用します)とポーリング期間を渡します。この期間は、OnStickイベントを繰り返し呼び出す時間間隔をミリ秒単位で指定します。pが0なら、ジョイスティックの状態が変化したときのみOnStickイベントが呼び出されます。pが0より大きい場合、サンプル時間間隔の終わりごとにOnStickイベントが呼び出されます。例:stick(1,5, windowfromnode(sv()), 200); は、200ミリ秒ごとにOnStickイベントが呼び出されるように設定します。このコマンドが動作するには、ビューにOnStick属性を追加する必要があります(ビューに属性を追加した後で、右クリック -> [編集]|[オブジェクトの属性を再バインドする]を使用して再バインドが必要な場合もあります)。
STICK_JOY_RELEASE_CAPTURE - このコマンドは、以前に5コマンドでキャプチャーしたウィンドウから、ジョイスティックのキャプチャーをリリースします。コマンド5と同様にwinパラメータを渡す必要があります。
STICK_JOY_RPOS - ジョイスティックのラダーまたは4番目の軸の現在の位置。ジョイスティックがz軸の周囲で回転できる場合、これは通常はジョイスティックの回転を示します。この値も、0から65535までの数値です。ゲームパッドを使用している場合、右側のジョイスティックのx位置です。
STICK_JOY_UPOS - ジョイスティックの5番目の軸の現在の位置。
STICK_JOY_VPOS - ジョイスティックの6番目の軸の現在の位置。
STICK_JOY_POV - ジョイスティックの視点コントロールの現在の位置。この値は0から35900までの数値で、度を100倍した数値を表します。ゲームパッドの場合、ゲームパッドの左側にある方向パッドを表します。上は0、右は9000、下は18000、左は27000です。方向パッドが押されていない場合、値は65535です。ジョイスティックを使用している場合、スティック自体に方向性サムコントローラがあり、上下左右に押せることがあります。このコマンドは、そのコントローラーの設定を取得します。
STICK_JOY_CURRENT_BUTTON - 現在押されているボタンの番号。
STICK_JOY_FLAGS - ジョイスティックについて有効な情報が返されていることを示すフラグ。
STICK_XBOX_STATUS - Xboxコントローラーの接続性を照会します。コントローラーが正しく接続されていれば、0を返します。
STICK_XBOX_BUTTONS - デバイスのデジタルボタンを示すビットマスク。セットされているビットは、対応するボタンが押されていることを意味します。
STICK_XBOX_LEFT_THUMB_X - 左側にあるサムスティックのx軸の値。サムスティックのそれぞれの軸メンバーは、-32768から32767までの符号付き数値で、サムスティックの位置を示します。値0は中央を示します。負の値は下または左を示します。正の値は上または右を示します。
STICK_XBOX_LEFT_THUMB_Y - 左側のサムスティックのy軸の値。値は-32768から32767までです。
STICK_XBOX_RIGHT_THUMB_X - 右側のサムスティックのx軸の値。値は-32768から32767までです。
STICK_XBOX_RIGHT_THUMB_Y - 右側のサムスティックのy軸の値。値は-32768から32767までです。
STICK_XBOX_LEFT_TRIGGER - 左側のトリガーアナログコントロールの現在の値。値は0から255までです。
STICK_XBOX_RIGHT_TRIGGER - 右側のトリガーアナログコントロールの現在の値。値は0から255までです。
STICK_VR_STATUS - Oculus Riftコントローラーがアクティブなら1を返します。HTC Viveコントローラーがアクティブなら2を返します。コントローラーが非アクティブなら0を返します。コントローラーがアタッチされていなければ、nullvarを返します。
STICK_VR_THUMB_X - サムスティックまたはトラックパッドのx軸の値で、-1から1までです。
STICK_VR_THUMB_Y - サムスティックまたはトラックパッドのy軸の値で、-1から1までです。
STICK_VR_INDEX_TRIGGER - インデックストリガーの値で、0から1までです。
STICK_VR_GRIP_TRIGGER - グリップトリガーの値で、0から1までです。HTC Viveでは、グリップボタンが押されています。
STICK_VR_BUTTON_1 - 最初のボタンが押されています。Oculus RiftではAまたはXです。HTC Viveでは使用されません。
STICK_VR_BUTTON_2 - 2番目のボタンが押されています。Oculus RiftではBまたはYです。HTC Viveでは使用されません。
STICK_VR_BUTTON_3 - 3番目のボタンが押されています。Oculus RiftではEnterまたはHomeです。HTC ViveではMenuです。
STICK_VR_BUTTON_4 - 4番目のボタンが押されています。Oculus Riftではサムスティックです。HTC Viveではトラックパッドです。
STICK_VR_TOUCH_BUTTON_1 - 最初のボタンがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_BUTTON_2 - 2番目のボタンがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_BUTTON_3 - 3番目のボタンがタッチされています。Oculus Riftでは使用されません。
STICK_VR_TOUCH_BUTTON_4 - 4番目のボタンがタッチされています。
STICK_VR_TOUCH_THUMB_REST - Oculus Riftのサムレストセンサーがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_INDEX_TRIGGER - インデックストリガーセンサーがタッチされています。
STICK_VR_TOUCH_POINTING - Oculus Riftでハンドジェスチャがポイントされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_THUMB_UP - Oculus Riftでハンドジェスチャがサムズアップされています。HTC Viveでは使用されません。
STICK_VR_HAND_POSITION - VR空間でのコントローラーの位置。
STICK_VR_HAND_ROTATION - VR回転座標でのコントローラーの回転。
STICK_VR_HAND_WORLD_POSITION - FlexSimのワールド空間でのコントローラーの位置。
STICK_VR_HAND_WORLD_ROTATION - FlexSim回転座標でのコントローラーの回転。
STICK_VR_HAND_OFFSET_POSITION - FlexSimのワールド空間でのコントローラーの位置ですが、コントローラーの回転に基づいてオフセットが適用されます。pパラメータには、オフセットベクトルとして配列を渡します。このオプションを使用して、コントローラーに対する相対ポイント、たとえば指の位置や、コントローラーのポイント先を取得できます。
STICK_VR_TARGET_FLOOR_POSITION - 床の上でコントローラーがポイントしている先の位置。pパラメータの値には、コントローラーからの最大距離を渡します。
STICK_VR_SET_VIBRATION - コントローラーを振動させます。Oculus Riftでは、pパラメータに配列を渡します。最初の要素は0から1までの値で、周波数を表します。2番目の要素は0から1までの値で、振幅を表します。HTC Viveでは、期間をミリ秒単位でpパラメータとして渡します。
STICK_VR_SUBMIT_VIBRATION - コントローラーを微振動させます。最初のOculus Touchコントローラーでは、pパラメータに振幅(0~255)の配列を渡し、この値がキューに入れられて実行されます。HTC ViveやOculus Rift Sコントローラーでは使用されません。
sticknoは、照会するジョイスティックやゲームパッドのidを定義します。0から32までの数値です。通常は、コンピュータに接続されているジョイスティックは1つだけなので、sticknoの値には1を使用します。ゲームパッドを使用する場合、sticknoに2を使用することが必要な場合もあります。Xboxコントローラーの場合、sticknoの値は0から3までです。VRコントローラーの場合、sticknoは0または1です。Oculusタッチコントローラーの場合、sticknoの0は左手、1は右手です。sticknoに-1を使用すると、接続されているVRヘッドセットのステータス、位置、回転を取得できます。
commandは、このコマンドで実行する動作を定義します。次のマクロのいずれかを使用します。
STICK_JOY_STATUS - ジョイスティックの接続性を照会します。ジョイスティックが正しく接続されていれば、このコマンドは0を返します。戻り値が0以外の場合、ジョイスティックの接続性に何らかのエラーがあり、どのようなエラーなのかをシステムコンソールで確認できます。次のエラーが発生する可能性があります。
MMSYSERR_NODRIVER - ジョイスティックのドライバーが存在しません。
MMSYSERR_INVALPARAM - ジョイスティックのIDが無効か、hwndがNULLです。
JOYERR_NOCANDO - 必要なサービス(Windowsタイマーなど)が使用できないため、ジョイスティックの入力をキャプチャーできません。
JOYERR_UNPLUGGED - 指定されたジョイスティックはシステムに接続されていません。
JOYERR_PARMS - ジョイスティックのIDが無効か、hwndがNULLです。
STICK_JOY_XPOS - ジョイスティックの現在のX座標。0から65535までの数値です。0はジョイスティックが左へいっぱいまで押されていることを、65535は右へいっぱいまで押されていることを、32768は正確に中央の位置にあることを示します。ゲームパッドを使用している場合、左側のジョイスティックのx位置です。
STICK_JOY_YPOS - ジョイスティックの現在のY座標。この値も、0から65535までの数値です。0は上方向、65535は下方向を意味します。ゲームパッドを使用している場合、ゲームパッドの左側にあるジョイスティックの位置です。
STICK_JOY_ZPOS - ジョイスティックの現在のZ座標。ジョイスティックを使用している場合、これは通常、ジョイスティックのスロットルの現在の設定です。この値も、0から65535までの数値です。ゲームパッドを使用している場合、右側のジョイスティックのy位置を表します。
STICK_JOY_BUTTONS - ジョイスティックの32のボタンの現在の状態。ビット単位の整数で、各ビットは与えられたボタンの現在の状態を表します。ジョイスティックの場合、メインのトリガーボタンは通常0x00000001ビット、スティックの他のボタンは0x00000002および0x00000004、ジョイスティックのベースにあるボタンはより上位のビットで表されます。ジョイスティックごとに多少異なるので、自分でテストすることが必要です。
STICK_JOY_SET_CAPTURE - このコマンドは、ジョイスティックのキャプチャーを、指定したFlexSimウィンドウに設定します。このコマンドにはwinとpのパラメータを渡す必要があります。このコマンドを実行すると、ビューのOnStick属性にジョイスティックのメッセージが送信されます。たとえば、正投影ビューでジョイスティックのイベントをリッスンする場合、このコマンドを呼び出し、正投影ビューのHWNDハンドル(windowfromnode()を使用します)とポーリング期間を渡します。この期間は、OnStickイベントを繰り返し呼び出す時間間隔をミリ秒単位で指定します。pが0なら、ジョイスティックの状態が変化したときのみOnStickイベントが呼び出されます。pが0より大きい場合、サンプル時間間隔の終わりごとにOnStickイベントが呼び出されます。例:stick(1,5, windowfromnode(sv()), 200); は、200ミリ秒ごとにOnStickイベントが呼び出されるように設定します。このコマンドが動作するには、ビューにOnStick属性を追加する必要があります(ビューに属性を追加した後で、右クリック -> [編集]|[オブジェクトの属性を再バインドする]を使用して再バインドが必要な場合もあります)。
STICK_JOY_RELEASE_CAPTURE - このコマンドは、以前に5コマンドでキャプチャーしたウィンドウから、ジョイスティックのキャプチャーをリリースします。コマンド5と同様にwinパラメータを渡す必要があります。
STICK_JOY_RPOS - ジョイスティックのラダーまたは4番目の軸の現在の位置。ジョイスティックがz軸の周囲で回転できる場合、これは通常はジョイスティックの回転を示します。この値も、0から65535までの数値です。ゲームパッドを使用している場合、右側のジョイスティックのx位置です。
STICK_JOY_UPOS - ジョイスティックの5番目の軸の現在の位置。
STICK_JOY_VPOS - ジョイスティックの6番目の軸の現在の位置。
STICK_JOY_POV - ジョイスティックの視点コントロールの現在の位置。この値は0から35900までの数値で、度を100倍した数値を表します。ゲームパッドの場合、ゲームパッドの左側にある方向パッドを表します。上は0、右は9000、下は18000、左は27000です。方向パッドが押されていない場合、値は65535です。ジョイスティックを使用している場合、スティック自体に方向性サムコントローラがあり、上下左右に押せることがあります。このコマンドは、そのコントローラーの設定を取得します。
STICK_JOY_CURRENT_BUTTON - 現在押されているボタンの番号。
STICK_JOY_FLAGS - ジョイスティックについて有効な情報が返されていることを示すフラグ。
STICK_XBOX_STATUS - Xboxコントローラーの接続性を照会します。コントローラーが正しく接続されていれば、0を返します。
STICK_XBOX_BUTTONS - デバイスのデジタルボタンを示すビットマスク。セットされているビットは、対応するボタンが押されていることを意味します。
STICK_XBOX_LEFT_THUMB_X - 左側にあるサムスティックのx軸の値。サムスティックのそれぞれの軸メンバーは、-32768から32767までの符号付き数値で、サムスティックの位置を示します。値0は中央を示します。負の値は下または左を示します。正の値は上または右を示します。
STICK_XBOX_LEFT_THUMB_Y - 左側のサムスティックのy軸の値。値は-32768から32767までです。
STICK_XBOX_RIGHT_THUMB_X - 右側のサムスティックのx軸の値。値は-32768から32767までです。
STICK_XBOX_RIGHT_THUMB_Y - 右側のサムスティックのy軸の値。値は-32768から32767までです。
STICK_XBOX_LEFT_TRIGGER - 左側のトリガーアナログコントロールの現在の値。値は0から255までです。
STICK_XBOX_RIGHT_TRIGGER - 右側のトリガーアナログコントロールの現在の値。値は0から255までです。
STICK_VR_STATUS - Oculus Riftコントローラーがアクティブなら1を返します。HTC Viveコントローラーがアクティブなら2を返します。コントローラーが非アクティブなら0を返します。コントローラーがアタッチされていなければ、nullvarを返します。
STICK_VR_THUMB_X - サムスティックまたはトラックパッドのx軸の値で、-1から1までです。
STICK_VR_THUMB_Y - サムスティックまたはトラックパッドのy軸の値で、-1から1までです。
STICK_VR_INDEX_TRIGGER - インデックストリガーの値で、0から1までです。
STICK_VR_GRIP_TRIGGER - グリップトリガーの値で、0から1までです。HTC Viveでは、グリップボタンが押されています。
STICK_VR_BUTTON_1 - 最初のボタンが押されています。Oculus RiftではAまたはXです。HTC Viveでは使用されません。
STICK_VR_BUTTON_2 - 2番目のボタンが押されています。Oculus RiftではBまたはYです。HTC Viveでは使用されません。
STICK_VR_BUTTON_3 - 3番目のボタンが押されています。Oculus RiftではEnterまたはHomeです。HTC ViveではMenuです。
STICK_VR_BUTTON_4 - 4番目のボタンが押されています。Oculus Riftではサムスティックです。HTC Viveではトラックパッドです。
STICK_VR_TOUCH_BUTTON_1 - 最初のボタンがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_BUTTON_2 - 2番目のボタンがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_BUTTON_3 - 3番目のボタンがタッチされています。Oculus Riftでは使用されません。
STICK_VR_TOUCH_BUTTON_4 - 4番目のボタンがタッチされています。
STICK_VR_TOUCH_THUMB_REST - Oculus Riftのサムレストセンサーがタッチされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_INDEX_TRIGGER - インデックストリガーセンサーがタッチされています。
STICK_VR_TOUCH_POINTING - Oculus Riftでハンドジェスチャがポイントされています。HTC Viveでは使用されません。
STICK_VR_TOUCH_THUMB_UP - Oculus Riftでハンドジェスチャがサムズアップされています。HTC Viveでは使用されません。
STICK_VR_HAND_POSITION - VR空間でのコントローラーの位置。
STICK_VR_HAND_ROTATION - VR回転座標でのコントローラーの回転。
STICK_VR_HAND_WORLD_POSITION - FlexSimのワールド空間でのコントローラーの位置。
STICK_VR_HAND_WORLD_ROTATION - FlexSim回転座標でのコントローラーの回転。
STICK_VR_HAND_OFFSET_POSITION - FlexSimのワールド空間でのコントローラーの位置ですが、コントローラーの回転に基づいてオフセットが適用されます。pパラメータには、オフセットベクトルとして配列を渡します。このオプションを使用して、コントローラーに対する相対ポイント、たとえば指の位置や、コントローラーのポイント先を取得できます。
STICK_VR_TARGET_FLOOR_POSITION - 床の上でコントローラーがポイントしている先の位置。pパラメータの値には、コントローラーからの最大距離を渡します。
STICK_VR_SET_VIBRATION - コントローラーを振動させます。Oculus Riftでは、pパラメータに配列を渡します。最初の要素は0から1までの値で、周波数を表します。2番目の要素は0から1までの値で、振幅を表します。HTC Viveでは、期間をミリ秒単位でpパラメータとして渡します。
STICK_VR_SUBMIT_VIBRATION - コントローラーを微振動させます。最初のOculus Touchコントローラーでは、pパラメータに振幅(0~255)の配列を渡し、この値がキューに入れられて実行されます。HTC ViveやOculus Rift Sコントローラーでは使用されません。
例
stick(1, STICK_JOY_YPOS); ジョイスティックid 1のy位置を取得します。
suspenddraw (num bitmask)
説明
開発者向けです。ビットマスク。ウィンドウタイプの描画を無効にします。ビット:0 - TREE、1 - PLANAR、2 - SPATIAL
例
suspenddraw(1)
switch_variable (obj object, str var[, num off/on])
説明
開発者向けです。動的スイッチ変数をオブジェクトに追加および設定、またはオブジェクトから削除します。onに設定するとき、varで指定される名前のノードがオブジェクトの構造体に追加され、数値1が割り当てられます。offに設定するとき、varで指定される名前のノードが存在すれば、オブジェクトの構造体から削除されます。モデル更新のコードで使用されます。
例
switch_variable(so(),"arrivalmode",1);
toggleallcodestates (node startpoint, num ascpp)
startpointの下にあるすべてのコードノードを、C++またはflexscriptとして切り替える
説明
startpointから開始してツリーを走査し、すべてのコードノードをc++またはflexscriptに切り替えます。1からc++に、0ならflexscriptに切り替えます。現在のコード状態にロックされていないノードのみが変更されます。メニューオプションの[構築]|[すべてのコードをC++にする]、または[構築]|[すべてのコードをFlexScriptにする]と同じ操作です。
例
toggleallcodestates(model(), 1);
tracemaskevents (num mask)
説明
開発者向けです。32ビットのトレースマスクとしてMath.pow(2,N1)+Math.pow(2,N2) の合計を設定します。ここでNxは、トレースで報告するイベント番号です。[表示]|[トレースデバッガー]を参照してください。
例
tracemaskevents(listsum(Math.pow(2,1),Math.pow(2,2),Math.pow(2,3)))
tracemaskobject (obj object)
説明
開発者向けです。トレースデバッガーのイベント報告に含めるオブジェクトを設定します。[表示]|[トレースデバッガー]を参照してください。
例
tracemaskobject(Model.find("Processor3"))
tracemasktime (num start, num end)
説明
開発者向けです。トレースデバッガーでのイベント報告の開始時間と終了時間を定義します。[表示]|[トレースデバッガー]を参照してください。
例
tracemasktime(100,200)
uselisteners (num mask)
説明
リスニングを有効または無効にします。
例
uselisteners(1)
描画
平面、正投影、または透視投影ビューでのグラフィックス描画に関連するコマンドです。描画コマンドは、オブジェクトの[プロパティ]ウィンドウにある[カスタム描画コード]フィールドなど、OnDrawイベントで使用するよう設計されています。
bindtexture (num textureid)
説明
この関数は、OpenGL呼び出しシーケンスで使用されます。シーンを描画するためOpenGLコマンドが使用されるとき、このコマンドはFlexSimにロードされるテクスチャをインデックスtextureidとバインドします。バインドされたテクスチャは、以後に描画されるポリゴンをレンダリングするため使用されます。テクスチャマッピングは、画像(またはテクスチャ)から、ポリゴンや他のグラフィックスプリミティブの表面への適用(またはマッピング)です。
例
bindtexture(10)
以後のポリゴンをレンダリングするため、インデックス番号10のロード済みテクスチャを使用します。
以後のポリゴンをレンダリングするため、インデックス番号10のロード済みテクスチャを使用します。
draw3dtext (str text[, num asBitmap])
3dビューにテキストを描画する
説明
このコマンドはdrawtext()と似ていますが、3Dビューでのみ使用でき、テキストのレンダリングプロシージャに直接アクセスできるようパラメータセットが削られています。drawtext()では現在のオブジェクトや、一部のOpenGL状態の変化に基づいて多少の自動スケーリングが行われるのに対して、draw3dtext()はテキスト描画プロシージャを直接呼び出すため、位置設定、スケーリング、色設定などはすべて、glTranslated()、glScaled()、glColor3d()などのOpenGLコマンドで行います。
例
draw3dtext(current.name);
drawbox (num x, num y, num z, num sx, num sy, num sz, num glbegin)
単純なボックスを描画する
説明
単純なボックスを描画します。glbeginが1なら、描画前にglBeginを呼び出します。このコマンドは、OpenGLタイプの立方体を描画するための早い方法で、ライティング、色、テクスチャをdrawcube()コマンドより細かく指定できます。
例
drawbox(5,0,0, 2,1,3, 1);
drawcolumn (num x, num y, num z, num totalsides, num baseradius, num topradius, num height, num rx, num ry, num rz, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex, num textureXrepeat, num textureYrepeat])
3Dの列を描画する
説明
複数の辺と高さを持つ、正方形、五角形、ピラミッドなど任意の形状を描画できる非常に多用途なコマンドで、円筒(辺の総数が多い場合)も描画できます。
x、y、zの位置を原点(基部の中央)として、列を描画します。この列は、辺の数、下端の半径、上端の半径、高さで定義されます。列はrx、ry、rzにより各軸の周囲で度単位に回転できます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、列は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が列の各面に沿ってtextureXrepeatおよびtextureYrepeat回だけ繰り返されます。
列の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
x、y、zの位置を原点(基部の中央)として、列を描画します。この列は、辺の数、下端の半径、上端の半径、高さで定義されます。列はrx、ry、rzにより各軸の周囲で度単位に回転できます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、列は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が列の各面に沿ってtextureXrepeatおよびtextureYrepeat回だけ繰り返されます。
列の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawcolumn(0,0,0, 5 ,4,2, 6 ,0,0,0, 175,175,175, .6, 3, 5,1);
drawcube (num x, num y, num z, num sx, num sy, num sz, num rx, num ry, num rz, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex, num textureXrepeat, num textureYrepeat])
3D立方体を描画する
説明
x、y、zの位置を原点(左下コーナー)として、立方体を描画します。長さ、幅、高さはそれぞれsx、sy、szで定義されます。rx、ry、rzを使用して、それぞれx、y、z軸の周囲に度単位で回転できます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、立方体は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が立方体の各面に沿ってtextureXrepeatおよびtextureYrepeat回だけ繰り返されます。
立方体の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか[ツール]|[メディアファイル]メニューを使用して得られる数値です。
オプションのopacityパラメータにより、立方体は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が立方体の各面に沿ってtextureXrepeatおよびtextureYrepeat回だけ繰り返されます。
立方体の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawcube(0,0,0, 5,3,2, 0,0,0, 175,175,175, .6, 3, 1,1);
drawcylinder (num x, num y, num z, num baseradius, num topradius, num height, num rx, num ry, num rz, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex])
3Dの円柱を描画する
説明
このコマンドは、x、y、zの位置を原点(基部の中央)として、中空の円柱を描画します。円柱の寸法は、基部の半径、上端の半径、高さで定義されます。円筒の先端を飾るには、drawdisk()コマンドを使用します。円柱は、rx、ry、rzを使用して、それぞれx、y、z軸の周囲に度単位で回転できます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、円柱は透明(0)から不透明(1)まで変化します。有効なtextureindexの数値が入力された場合、関連付けられている画像が円柱の外周に沿ったテクスチャとして使用されます。
円柱の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
オプションのopacityパラメータにより、円柱は透明(0)から不透明(1)まで変化します。有効なtextureindexの数値が入力された場合、関連付けられている画像が円柱の外周に沿ったテクスチャとして使用されます。
円柱の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawcylinder(0,0,0, 1,1, 5, 0,0,0, 175,175,175, .6,3);
drawdisk (num x, num y, num z, num innerradius, num outerradius, num startangle, num sweepangle, num rx, num ry, num rz, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex])
3Dの円盤を描画する
説明
x、y、zの位置を原点(半径の中央)として、平坦な円盤を描画します。円盤の寸法は内側の半径、外側の半径、開始角度、掃引角度で定義されます。掃引角度が360なら、完全な円が描画されます。innerradiusが0より大きいなら、円盤の中央に穴が開けられます。円盤は、rx、ry、rzを使用して、それぞれx、y、z軸の周囲に度単位で回転できます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、円盤は透明(0)から不透明(1)まで変化します。有効なtextureindexの数値が入力された場合、関連付けられている画像が円盤の表面に沿ったテクスチャとして使用されます。
円盤の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
オプションのopacityパラメータにより、円盤は透明(0)から不透明(1)まで変化します。有効なtextureindexの数値が入力された場合、関連付けられている画像が円盤の表面に沿ったテクスチャとして使用されます。
円盤の位置、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawdisk(0,0,0, .5,2, 90,270, 0,0,0, 175,175,175, 1,3);
drawflattext (str text)
説明
このコマンドは、3Dビューでのみ使用できます。テクスチャマッピングされたテキスト文字列を描画します。下のオブジェクトの名前と統計情報を描画するのと同じ機能が使用されます。正しくスケーリングされれば、非常に鮮明で読み取りやすいテキストが描画されます。このコマンドをsetdrawnamefunction()と組み合わせて使用すると、オブジェクトの下のボックスに描画されるデータをカスタマイズできます。drawtext()とは異なり、このコマンドのパラメータセットは大幅に削られているため、テキストを描画する前に場所、サイズ、レンダリング設定をセットアップするにはglコマンド(fglTranslate()、fglScale()、fglColor()など)を使用します。
例
オブジェクトのカスタム描画コードトリガーに、次のコードを追加します。
if(!param(2)) {
setdrawnamefunction(80, 15, c, param(1), 1);
} else {
fglTranslate(-40, -15, 0);
drawflattext("Hello World");
}
drawfont (num font)
drawtext()で使用するフォントを指定する
説明
drawtextを呼び出す前に、描画するフォントを定義します。drawtextを呼び出した後で、フォントはデフォルトにリセットされます。現在使用できるフォントタイプは12(番号0から11まで)です。
例
drawfont(2)
drawimage (obj view, str imagepath, num x, num y, num width, num height, num scaling)
画像を描画する
説明
ビューのimagepathに画像を描画します。scalingの値は、画像をどのように配置およびスケーリングするかを指定します。
NO_SCALE(または0):画像のサイズと同じ幅と高さで、場所x、yに画像を描画します。
SCALE_DOWN:x、y、width、heightにより作成される長方形に画像を描画します。必要なら、この長方形に収まるように比率を維持して画像を縮小します。
SCALE_UP_DOWN:x、y、width、heightにより作成される長方形に画像を描画します。必要なら、この長方形に収まるように比率を維持して画像を拡大縮小します。
SCALE_INDEPENDENT:x、yの場所に、widthとheightのサイズの画像を描画します。
NO_SCALE(または0):画像のサイズと同じ幅と高さで、場所x、yに画像を描画します。
SCALE_DOWN:x、y、width、heightにより作成される長方形に画像を描画します。必要なら、この長方形に収まるように比率を維持して画像を縮小します。
SCALE_UP_DOWN:x、y、width、heightにより作成される長方形に画像を描画します。必要なら、この長方形に収まるように比率を維持して画像を拡大縮小します。
SCALE_INDEPENDENT:x、yの場所に、widthとheightのサイズの画像を描画します。
例
drawimage(c, "buttons\\visible_eye.png", 0, 10, 0, 0, 0);
drawline (obj view, num x1, num y1, num z1, num x2, num y2, num z2, num red {0-1}, num green {0-1}, num blue {0-1})
平面ラインを描画する
説明
このコマンドは、開始位置がxloc1、yloc1、zloc1で、終了位置がxloc2、yloc2、zloc2の平面ラインを描画します。色は赤、緑、青の色コンポーネント(0~1)で定義されます。
例
drawline(view, 0, 0, 0, 2, 2, 2, 1, 0, 0);
この例は、ポイント(0,0,0)からポイント(2,2,2)にラインを描画します。ラインの色は赤です。
この例は、ポイント(0,0,0)からポイント(2,2,2)にラインを描画します。ラインの色は赤です。
drawobject (obj view, num shapeindex, num textureindex[, num animation, treenode shapedata])
3D形状を描画する
説明
指定された形状とテクスチャインデックスを使用して3dオブジェクトを描画します。
例
drawtomodelscale(current);
drawobject(view,getshapeindex("fs3d//texturebox.wrl"),gettextureindex("flexsim.bmp"));
描画スケールをモデルのものに設定してから、flexsim.bmpをテクスチャとして使用し、texturebox.wrl形状を描画します。
drawobject(view,getshapeindex("fs3d//texturebox.wrl"),gettextureindex("flexsim.bmp"));
描画スケールをモデルのものに設定してから、flexsim.bmpをテクスチャとして使用し、texturebox.wrl形状を描画します。
drawpie (obj view, num x, num y, num z, num x2, num y2, num z2, num startangle, num endangle, num red {0-1}, num green {0-1}, num blue {0-1})
平坦な扇形を描画する
説明
[x1,y1,z1]と[x2,y2,z2]の中点を原点(半径の中心)として、平坦な扇形を描画します。角度は正のx軸から反時計回りに、度単位で測定されます。負の角度は時計回りに測定されます。扇形は、開始角度から反時計回りに終了角度までを占めます。色は赤、緑、青の色コンポーネント(0~1)で定義されます。
例
drawpie(view,3,3,0,0,0,0,45,90,0.5,0,0);
drawquad (obj view, num x1, num y1, num z1, num x2, num y2, num z2, num x3, num y3, num z3, num x4, num y4, num z4, num red {0-1}, num green {0-1}, num blue {0-1})
平坦な四辺形を描画する
説明
このコマンドは、x1、y1、z1、x2、y2、z2、x3、y3、z3、x4、y4、z4により定義される頂点を持つ平坦な四辺形を描画します。色は赤、緑、青の色コンポーネント(0~1)で定義されます。結果として得られる形状と照明は、頂点が定義される順序やシーケンスによって異なります。頂点がすべて同じ平面に属する場合、drawrectangle()コマンドの使用を検討してください。
例
drawquad(view, 0, 0, 1, 0, 0, 0, 2, 2, 2, 4, 5, 6, 1, 0, 0);
この例は、(0,0,0)、(1,0,0)、(2,2,2)、(4,5,6)の4つのポイントで定義された頂点を持つ四辺形を描画します。四辺形の色は赤です。
この例は、(0,0,0)、(1,0,0)、(2,2,2)、(4,5,6)の4つのポイントで定義された頂点を持つ四辺形を描画します。四辺形の色は赤です。
drawrect (obj view, num x1, num y1, num z1, num x2, num y2, num z2, num red {0-1}, num green {0-1}, num blue {0-1})
平坦な長方形を描画する
説明
このコマンドは、x1、y1、z1およびx2、y2、z2で定義された対角のコーナーを持つ、平坦な長方形を描画します。どちらのポイントも、xy平面と平行な平面に存在する必要があります。色は赤、緑、青の色コンポーネント(0~1)で定義されます。このコマンドは、平面、3D、グラフ、パネルのビューから呼び出すことができます。drawquad()も参照してください。
例
drawrect(view, 0, 0, .5, 1, 1, .5, 1, 0, 0);
対角コーナー(0,0,.5)および(1,1,.5)を使用して赤色の長方形を描画します。
対角コーナー(0,0,.5)および(1,1,.5)を使用して赤色の長方形を描画します。
drawrectangle (num x, num y, num z, num length, num width, num rx, num ry, num rz, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex, num textureXrepeat, num textureYrepeat])
3Dの長方形を描画する
説明
ユーザー定義の場所、長さ、幅、回転、色を使用して、平坦な長方形を描画します。x、y、z平面と並行でない長方形を描画するには、drawquad()コマンドを使用する必要があります。
オプションのopacityパラメータにより、長方形は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が長方形の表面にテクスチャとして、textureXrepeatおよびtextureYrepeat回だけ繰り返されます。
長方形の場所、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
オプションのopacityパラメータにより、長方形は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が長方形の表面にテクスチャとして、textureXrepeatおよびtextureYrepeat回だけ繰り返されます。
長方形の場所、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawrectangle(0,0,0, 2,3, 0,0,0, 175,175,175, .6, 1, 2,3);
drawshadow (num phase (1,2,3))
OnDraw内でシャドーボリュームを描画する
説明
OnDraw内でシャドーボリュームを描画します。
例
drawshadow(1);
drawsphere (num x, num y, num z, num radius, num red {0-255}, num green {0-255}, num blue {0-255} [, num opacity {0-1}, num textureindex])
3Dの球を描画する
説明
x、y、zの場所を原点(球の中央)として、中空の球を描画します。球の寸法は、単一の半径により定義されます。色は赤、緑、青の色コンポーネント(0~255)で定義されます。
オプションのopacityパラメータにより、球は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が球の表面にテクスチャとして貼り付けられます。
球の場所、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
オプションのopacityパラメータにより、球は透明(0)から不透明(1)まで変化します。有効なtextureindex番号が入力された場合、関連付けられている画像が球の表面にテクスチャとして貼り付けられます。
球の場所、サイズ、回転はデフォルトで、描画の基礎となるオブジェクトに相対です。角括弧[]内に示されているオプションパラメータは、すべて使用するか、どれも使用しないか、どちらかにする必要があります。textureindexは、gettextureindex()コマンドか、[ツール]|[メディアファイル]メニューを使用して得られる数値です。
例
drawsphere(0,0,0,5,175,175,175,1,3);
drawtext (obj view, str text, num x, num y, num z [, num width, num height, num thickness, num rx, num ry, num rz, num red {0-1}, num green {0-1}, num blue {0-1} , num opacity {0-1}, num flags])
テキストを描画する
説明
このコマンドは、x、y、zにより定義される場所にテキストを描画します。widthパラメータは使用されません。テキストの幅と高さは、heightパラメータにより決定されます。回転はrx、ry、rzにより定義されます。色は赤、緑、青の色コンポーネント(0~1)で定義されます。flagsパラメータは次のように定義できます:0x1 = 太字、0x2 = 斜体、0x4 = 下線。flagsパラメータは3d以外のビューにのみ適用されます。opacityが使用される場合、0(完全に透明)から1(不透明)までの数値です。必要なら、drawtext()の前にdrawfont()コマンドを呼び出してフォントタイプを変更できます。このコマンドは、平面、3D、グラフ、パネルのビューで使用できます。
例
drawtext(view, "Hello", 0,0,0, 0,.3,.1, 90,0,0, 1,0,0, .8);
この例は、場所(0,0,0)にサイズ0.3、太さ0.1、回転(90,0,0)、rgb色(1,0,0)、不透明度0.8で「Hello」と描画します。
この例は、場所(0,0,0)にサイズ0.3、太さ0.1、回転(90,0,0)、rgb色(1,0,0)、不透明度0.8で「Hello」と描画します。
drawtomodelscale (obj object)
モデルの現在の描画スケールを取得する
説明
以前にdrawtoobjectscale()を呼び出してモデルに設定された、現在の描画スケールを返します。これは、次のOpenGL関数と同じです。
glScalef(1/object.location.x,1/object.location.y,1/object.location.z);
glScalef(1/object.location.x,1/object.location.y,1/object.location.z);
例
drawtomodelscale(current);
drawtoobjectscale (obj object)
以後の描画コマンドをオブジェクトのサイズに応じてスケーリングする
説明
このコマンドを使用すると、以後のすべての描画コマンドは、オブジェクトのサイズに応じてスケーリングされます。これは、次のOpenGL関数と同じです。
glScalef(object.location.x,object.location.y,object.location.z);
デフォルトでは、最初はオブジェクトのスケールに設定されます。
glScalef(object.location.x,object.location.y,object.location.z);
デフォルトでは、最初はオブジェクトのスケールに設定されます。
例
drawtoobjectscale(current);
drawtriangle (obj view, num x1, num y1, num z1, num x2, num y2, num z2, num x3, num y3, num z3, num red {0-1}, num green {0-1}, num blue {0-1})
平坦な三角形を描画する
説明
このコマンドは、xloc1、yloc1、zloc1、xloc2、yloc2、zloc2、xloc3、yloc3、zloc3により定義される頂点を持つ平坦な三角形を描画します。色は赤、緑、青の色コンポーネント(0~1)で定義されます。
例
drawtriangle(view, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0);
この例は、(0,0,0)、(1,0,0)、(0,1,0)の3つのポイントで定義された頂点を持つ三角形を描画します。 三角形の色は赤です。
この例は、(0,0,0)、(1,0,0)、(0,1,0)の3つのポイントで定義された頂点を持つ三角形を描画します。 三角形の色は赤です。
fglColor (num red {0-1}, num green {0-1}, num blue {0-1}[, num alpha {0-1}])
OpenGLでグリッドを描画する色を設定する
説明
OpenGLでグリッドを描画する色を設定します。rgbの色コンポーネントは0~1です。オプションのalphaコンポーネントは、0(透明)から1(不透明)までです。
例
fglDisable (num setting)
OpenGLの描画設定を無効にする
説明
OpenGLの描画設定を無効にします。描画設定のリストについては、glEnable()を参照してください。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglDisable(GL_LIGHTING);
fglEnable (num setting)
OpenGLの描画設定を有効にする
説明
OpenGLの描画設定を有効にします。FlexSimの描画エンジンは最適化のため、与えられた設定の有効/無効の状態を自動的に復元しないので、描画機能を実行した後でこのコマンドを使用し、設定をデフォルトに戻す必要があることに注意してください。設定をデフォルトに戻さないと、モデルの他のオブジェクトが正常にレンダリングされません。
OpenGLの一般的な描画設定には次のものがあります。
GL_LIGHTING
照明をオン/オフにします。
ポリゴンがビューアから離れても色が変わらない場合は、オンにします。
デフォルトは有効です。
GL_CULL_FACE
背面の除外をオン/オフにします。
ポリゴンの両面(前面と背面)を描画する場合はオフにします。
デフォルトは無効です。
GL_TEXTURE_2D
テクスチャ処理をオン/オフにします。
テクスチャが必要ない場所に表示されている場合はオフにします。
デフォルトは有効です。
さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントでglEnable()を参照してください。
OpenGLの一般的な描画設定には次のものがあります。
GL_LIGHTING
照明をオン/オフにします。
ポリゴンがビューアから離れても色が変わらない場合は、オンにします。
デフォルトは有効です。
GL_CULL_FACE
背面の除外をオン/オフにします。
ポリゴンの両面(前面と背面)を描画する場合はオフにします。
デフォルトは無効です。
GL_TEXTURE_2D
テクスチャ処理をオン/オフにします。
テクスチャが必要ない場所に表示されている場合はオフにします。
デフォルトは有効です。
さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントでglEnable()を参照してください。
例
fglEnable(GL_LIGHTING);
fglinfo (num operation, obj view)
3Dビューの描画状態についての情報を取得する
説明
このコマンドを使用して、3dビューの描画状態について各種の情報にアクセスできます。実行されるロジックや、返されるデータは、動作パラメータに基づき、次のように決定されます。
FGL_INFO_SHADERTYPE - 描画パスのどの部分が実行されているか、たとえばシャドーマップのレンダリング(SHADERTYPE_RENDER_SHADOWS)、シャドーマップのぼかし処理(SHADERTYPE_BLUR)、オブジェクトの画面へのレンダリング(SHADERTYPE_DEFAULT)などを返します。
FGL_INFO_SHADERTYPE - 描画パスのどの部分が実行されているか、たとえばシャドーマップのレンダリング(SHADERTYPE_RENDER_SHADOWS)、シャドーマップのぼかし処理(SHADERTYPE_BLUR)、オブジェクトの画面へのレンダリング(SHADERTYPE_DEFAULT)などを返します。
例
/*シャドーマップをレンダリングするときはこのオブジェクトを描画しないこと*/
if (fglinfo(FGL_INFO_SHADERTYPE, view) == SHADERTYPE_RENDER_SHADOWS)
return 0;
if (fglinfo(FGL_INFO_SHADERTYPE, view) == SHADERTYPE_RENDER_SHADOWS)
return 0;
fglLoadIdentity ()
説明
現在のOpenGL描画コンテキストに識別マトリクスをロードします。言い換えると、現在のマトリクスを識別マトリクスに置き換えます。マトリクスは、n次元変換を1つのパッケージで指定する方法です。識別マトリクスをロードすることで、指定を原点にリセットし、回転、平行移動、スケーリングを解除できます。デフォルトの位置は(0,0,0)で、デフォルトの方向はz軸の負の方向です。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglLoadIdentity()
fglMatrixMode (num mode)
以後のマトリクス演算について、どのマトリクススタックが対象かを指定する
説明
以後のマトリクス演算について、どのマトリクススタックが対象かを指定します。マトリクスは、n次元変換を1つのパッケージで指定する方法です。受け付けられる値は、GL_MODELVIEW、GL_PROJECTION、GL_TEXTUREの3つです。初期値はGL_MODELVIEWで、シーン内でオブジェクトを移動するとき使用されます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglMatrixMode(GL_MODELVIEW);
fglNormal (num x, num y, num z)
OpenGLで以後の頂点のシェーディングを行うための法線ベクトルを設定する
説明
OpenGL描画で以後の頂点のシェーディングを行うための法線ベクトルを設定します。ポリゴンは、法線が適用されない限りフラットシェーディングされます。法線はポリゴンに対して垂直なベクトルで、ポリゴンの向いている方向を指すものです。頂点が反時計回りの順序で定義されているポリゴンは、「右手の法則」に従って前方を指すことに注意してください。ポリゴンのシェーディングは、法線と光源の間の角度に基づいて行われます。法線はそれぞれの頂点に対して、色と同様な方法で適用されますが、通常は単に各ポリゴンの定義の最初で定義されます。ポリゴンの法線が光源に直接向いている場合は明るくシェーディングされ、角度が傾斜している場合は暗くシェーディングされます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglNormal(1,0,0);
fglPopMatrix ()
マトリクススタックから現在のOpenGL描画コンテキストをポップする
説明
マトリクススタックから現在のOpenGL描画コンテキストをポップします。すなわち、スタックの一番上にある空間に戻ります。OpenGLスタックでは、空間マトリクスがLIFOの順序で保存されます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglPopMatrix();
fglPushMatrix ()
現在のOpenGL描画コンテキストをマトリクススタックにプッシュする
説明
現在のOpenGL描画コンテキストをマトリクススタックにプッシュします。プッシュしたコンテキストは、後でglPopMatrix()を使用して取得できます。複数のオブジェクトを描画するとき、glTranslated、glRotated、glScaledが次のオブジェクトに影響することが望ましくない場合は、glPushMatrixとglPopMatrixを使用します。OpenGLスタックでは、空間マトリクスがLIFOの順序で保存されます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglPushMatrix();
fglRotate (num degrees, num x, num y, num z)
現在のOpenGL描画コンテキストを、x、y、z軸の周囲でdegreesだけ回転する
説明
現在のOpenGL描画コンテキストを、頂点(x,y,z)により定義される軸の周囲でdegreesだけ回転します。回転後は、すべてが軸の新しい回転に基づいて描画されます。OpenGLのxyz座標系の定義については、glVertex3dを参照してください。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglRotate(90,1,0,0);
fglScale (num x, num y, num z)
現在のOpenGL描画コンテキストをx、y、z方向にスケーリングする
説明
現在のOpenGL描画コンテキストを、与えられたスケールパラメータに従ってスケーリングします。OpenGLのxyz座標系の定義については、glVertex3dを参照してください。このコマンドの後では、すべてが変更後の軸のスケールに基づいて描画されます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglScale(2,4,1);
fglTranslate (num x, num y, num z)
現在のOpenGL描画コンテキストをx、y、zだけ平行移動する
説明
現在のOpenGL描画コンテキストを、与えられた平行移動パラメータに従って変更移動します。OpenGLのxyz座標系の定義については、glVertex3dを参照してください。平行移動後は、すべてが軸の新しい場所に基づいて描画されます。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
fglTranslate(15, 4, 0);
getdrawtextmetric (str text, num fontsize, num metric[, num a])
説明
テキストについての情報を返します。metricが1なら、テキストの幅が返されます。metricが2なら、テキストの高さが返されます。metricが3なら、「a」を最大範囲として、収められるテキストの最大の長さが返されます。
例
getdrawtextmetric("Hello",12,1,0);
glIsEnabled (num setting)
OpenGL設定が有効なら1を、そうでなければ0を返す
説明
OpenGL設定が有効なら1を、そうでなければ0を返します。描画設定のリストについては、fglEnable()を参照してください。この操作は非常に低速で、推奨されないことに注意してください。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
glIsEnabled(GL_LIGHTING)
glLineWidth (num linewidth)
OpenGLで以後に描画されるラインの線幅を指定する
説明
OpenGLで以後に描画されるラインの線幅を指定します。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
glLineWidth(3);
glPointSize (num pointsize)
OpenGLで以後に描画される頂点のポイントサイズをピクセル単位で指定する
説明
OpenGLで以後に描画される頂点のポイントサイズを、ピクセル単位で指定します。さらに詳細な情報が必要な場合は、標準のOpenGLドキュメントを参照してください。
例
glPointSize(5);
mesh (node meshnode, int pervertexattribs, int flags)
空白のグリッドを作成してmeshnodeに割り当てる
説明
空白のグリッドを作成してmeshnodeに割り当てます。pervertexattribsは、次の属性をビット単位でORした値です。
MESH_POSITION(デフォルトで追加されます)
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
flagsは次のいずれかです。
MESH_STATIC_DRAW
MESH_DYNAMIC_DRAW
MESH_INDEXED
MESH_POSITION(デフォルトで追加されます)
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
flagsは次のいずれかです。
MESH_STATIC_DRAW
MESH_DYNAMIC_DRAW
MESH_INDEXED
例
mesh(Model.find("mesh"), MESH_NORMAL | MESH_DIFFUSE, MESH_STATIC_DRAW)
meshaddindex (node meshnode, int index)
インデックス付き頂点をグリッドに追加する
説明
インデックス付き頂点を、meshnodeに関連付けられているグリッドに追加します。グリッドにMESH_INDEXEDフラグがない場合、このコマンドは無視されます。
例
int newindex = meshaddindex(node("/mesh",model()), 4)
meshaddvertex (node meshnode)
頂点をグリッドに追加する
説明
頂点を、meshnodeに関連付けられているグリッドに追加します。
追加された頂点のインデックスを返します。
追加された頂点のインデックスを返します。
例
meshaddvertex(Model.find("mesh"))
meshdraw (node meshnode, int drawmode, int offset, int count [, int stride])
グリッドを描画する
説明
meshnodeに関連付けられているグリッドを描画します。drawmodeの値は次のいずれかです。
GL_POINTS
GL_LINES
GL_LINE_LOOP
GL_TRIANGLES
GL_TRIANGLE_STRIP
GL_TRIANGLE_FAN
offsetは、頂点インデックスの開始番号を示します。countは、いくつの頂点にdrawmodeを設定するかを指定します。strideは、いくつの頂点インデックスを中間でスキップするかを指定します。
インデックス付きグリッドの場合、strideは無視されます。
GL_POINTS
GL_LINES
GL_LINE_LOOP
GL_TRIANGLES
GL_TRIANGLE_STRIP
GL_TRIANGLE_FAN
offsetは、頂点インデックスの開始番号を示します。countは、いくつの頂点にdrawmodeを設定するかを指定します。strideは、いくつの頂点インデックスを中間でスキップするかを指定します。
インデックス付きグリッドの場合、strideは無視されます。
例
meshdraw(node("/mesh",model()), GLTRIANGLES, 0, 3, 0)
meshinfo (node meshnode, int type[,int index, int param])
グリッドから指定の情報を取得する
説明
meshnodeに関連付けられているグリッドから、指定の情報を取得します。indexは、要求される頂点のインデックスです(0から開始)。typeは、グリッドについて次のいずれかを指定します(indexとparamは無視されます)。
MESH_PER_VERTEX_ATTRIBS
MESH_PER_MESH_ATTRIBS
MESH_FLAGS
MESH_NR_VERTS
MESH_GET_INDEX - 与えられたインデックスについて頂点インデックスを返します(MESH_INDEXEDフラグと併用した場合のみ有効)。
次に示すのは頂点に固有のタイプです。
MESH_POSITION
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
頂点を指定する場合、paramに次のものが有効です。
MESH_COLOR_RED
MESH_COLOR_GREEN
MESH_COLOR_BLUE
MESH_COLOR_ALPHA
MESH_POS_X
MESH_POS_Y
MESH_POS_Z
MESH_TEX_S
MESH_TEX_T
MESH_PER_VERTEX_ATTRIBS
MESH_PER_MESH_ATTRIBS
MESH_FLAGS
MESH_NR_VERTS
MESH_GET_INDEX - 与えられたインデックスについて頂点インデックスを返します(MESH_INDEXEDフラグと併用した場合のみ有効)。
次に示すのは頂点に固有のタイプです。
MESH_POSITION
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
頂点を指定する場合、paramに次のものが有効です。
MESH_COLOR_RED
MESH_COLOR_GREEN
MESH_COLOR_BLUE
MESH_COLOR_ALPHA
MESH_POS_X
MESH_POS_Y
MESH_POS_Z
MESH_TEX_S
MESH_TEX_T
例
double xposition = meshinfo(Model.find("mesh"), MESH_POSITION, 6, MESH_POS_X)
meshsetattrib (node meshnode, int attribid, double param1 [, double param2, double param3, double param4])
attribidの値をグリッドのvertindexに追加/設定する
説明
attribidの値を、meshnodeに関連付けられているグリッド全体に適用します。attribidには次の属性を使用できます。
MESH_NORMAL
MESH_AMBIENT
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
MESH_SPECULAR
MESH_SHININESS
MESH_EMISSIVE
MESH_NORMAL
MESH_AMBIENT
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
MESH_SPECULAR
MESH_SHININESS
MESH_EMISSIVE
例
meshsetattrib(Model.find("mesh"), 1, MESH_DIFFUSE4, 1, 0, 0, 1)
meshsetvertexattrib (node meshnode, int vertindex, int attribid, double param1 [, double param2, double param3, double param4])
attribidの値をグリッドのvertindexに設定する
説明
attribidの値を、meshnodeに関連付けられているグリッドのvertindexに設定します。attribidには次の属性を使用できます。
MESH_POSITION
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
注意:attribidは、グリッドを作成するより前に定義されている必要があります。
MESH_POSITION
MESH_TEX_COORD2
MESH_NORMAL
MESH_DIFFUSE
MESH_DIFFUSE4
MESH_AMBIENT_AND_DIFFUSE
MESH_AMBIENT_AND_DIFFUSE4
注意:attribidは、グリッドを作成するより前に定義されている必要があります。
例
mesh(Model.find("mesh"), MESH_NORMAL | MESH_DIFFUSE4, MESH_STATIC_DRAW)
meshsetvertexattrib(Model.find("mesh"), 1, MESH_DIFFUSE4, 1, 0, 0, 1)
meshsetvertexattrib(Model.find("mesh"), 1, MESH_DIFFUSE4, 1, 0, 0, 1)
setdrawnamefunction (num boxwidth, num boxheight, node nodefunction[, num pval1, num pval2, num pval3])
説明
このコマンドを使用して、モデルでオブジェクトの下のボックスに情報を表示する機能に直接アクセスできます。FlexSimの3D表示メカニズムでは、モデル内のオブジェクトに対して複数の描画パスを実行します。最初に、描画が必要なデータを収集してキャッシュします。次に、各オブジェクトについてオブジェクトの形状を描画し、オブジェクトのカスタム描画機能を呼び出します。最後に、コネクターや情報ボックスなどのオーバーレイを描画します。オブジェクトのカスタム描画機能の一部、すなわちOnDrawイベントやオブジェクトのカスタム描画コードトリガーとしてsetdrawnamefunction()コマンドが呼び出された場合、そのオブジェクトの情報ボックスのステップに描画シーケンスが到達したときにコールバックが起動されます。このためには、コマンドを呼び出して描画するボックスのサイズを指定し、ボックス情報を描画するため起動されるコードを保持しているノードへの参照をnodefunctionパラメータとして渡し、最大3つのパラメータをparam(1)、param(2)、param(3)としてnodefunctionに渡します。その後で、drawflattext()コマンド、または他の任意のOpenGL描画コマンドを使用して、必要な情報を描画するnodefunctionコードを実装します。nodefunctionが呼び出されるとき、OpenGLのモデルビューマトリクスは、(0,0,0)のポイントが表示ボックスの上端中央で、長さの1単位が画面の1ピクセルに相当するよう設定されることに注意してください。
例
オブジェクトのカスタム描画コードトリガーに、次のコードを追加します。
if(!param(2)) {
setdrawnamefunction(80, 15, c, param(1), 1);
} else {
fglTranslate(-40, -15, 0);
drawflattext("Hello World");
}
spacebase ([num view/object])
説明
OpenGLマトリクスを、現在のobject/viewのスケーリングされた空間に設定します。パラメータが0なら、オブジェクトのベース空間マトリクスがロードされます。パラメータが1なら、ビューの空間がロードされ、以後のすべての描画コマンドは直接ビューアの方角を向き、スケールは変更されません。このコマンドは、OnDrawイベントとカスタム描画コードトリガーでのみ使用できます。OpenGL空間をオブジェクトのサイズでスケーリングするには、drawtoobjectscale()を参照してください。
例
spacebase(0);
spacerotate (num x, num y, num z)
説明
OpenGL空間に回転を適用します。これは、次のOpenGLコードに相当します(OpenGLの座標系ではyがFlexSimのz軸の方向、zはFlexSimのy軸の方向を指すことに留意してください)。
glRotatef( z, 0.0f, 1.0f, 0.0f);
glRotatef(-y, 0.0f, 0.0f, 1.0f);
glRotatef( x, 1.0f, 0.0f, 0.0f);
glRotatef( z, 0.0f, 1.0f, 0.0f);
glRotatef(-y, 0.0f, 0.0f, 1.0f);
glRotatef( x, 1.0f, 0.0f, 0.0f);
例
spacerotate(90, 0, 0)
現在の座標空間を、FlexSimのx軸の周囲で90度回転します。以後の描画コマンドは、新しい回転に合わせて実行されます。
現在の座標空間を、FlexSimのx軸の周囲で90度回転します。以後の描画コマンドは、新しい回転に合わせて実行されます。
spacescale (num x, num y, num z)
説明
OpenGL空間にスケール変換を適用します。これは、次のOpenGLコードに相当します(OpenGLの座標系ではyがFlexSimのz軸の方向、zはFlexSimのy軸の方向を指すことに留意してください)。
glScalef(x,z,y);
glScalef(x,z,y);
例
spacescale(2, 1, 1)
現在の座標空間を、FlexSimのx方向に2倍にスケーリングします。以後の描画コマンドは、新しいスケールに合わせて実行されます。
現在の座標空間を、FlexSimのx方向に2倍にスケーリングします。以後の描画コマンドは、新しいスケールに合わせて実行されます。
spacetranslate (num x, num y, num z)
説明
OpenGL空間に平行移動を適用します。これは、次のOpenGLコードに相当します(OpenGLの座標系ではyがFlexSimのz軸の方向、zはFlexSimのy軸の方向を指すことに留意してください)。
glTranslatef(x,z,-y);
glTranslatef(x,z,-y);
例
spacetranslate(current.size.x, -current.size.y, 0)
以前に平行移動が適用されていなければ、オブジェクトの左下コーナーに平行移動します。以後の描画コマンドは、新しい場所に合わせて実行されます。
以前に平行移動が適用されていなければ、オブジェクトの左下コーナーに平行移動します。以後の描画コマンドは、新しい場所に合わせて実行されます。
textureaxis_s (num x, num y, num z, num a)
説明
OpenGLの呼び出しシーケンスでテクスチャをバインドした後で、テクスチャの座標を指定できます。OpenGLは、マッピングにテクスチャ座標の概念を使用します。この関数は、テクスチャのS軸を設定するため使用されます。設定されたテクスチャの軸は、以後に描画されるすべてのポリゴンをレンダリングするため使用されます。
例
textureaxis_s(1,0,0,0)
textureaxis_t (num x, num y, num z, num a)
説明
OpenGLの呼び出しシーケンスでテクスチャをバインドした後で、テクスチャの座標を指定できます。OpenGLは、マッピングにテクスチャ座標の概念を使用します。この関数は、テクスチャのT軸を設定するため使用されます。設定されたテクスチャの軸は、以後に描画されるすべてのポリゴンをレンダリングするため使用されます。
例
textureaxis_t(0,0,1,0)
イベント
イベントの作成、検索、操作に使用されるコマンド。
addtoeventtypelegend (str name, num parameter, num value, str legendname)
説明
eventtypeの凡例では、そのeventtypeで特定のパラメータに与えられた値と、文字列とを関連付けできます。「parameter」に負の数値を渡すと、パラメータの説明として、前に指定した文字列を追加できます。「parameter」が負の値で「value」が-1なら、その数値はノードへのポインターと見なされ、ノードのパスが文字列として表示されます。
例
addtoeventtypelegend(index,-1,-1,"resource: "); // p1について「resource: 」というテキストを表示し、オブジェクトのパスを表示する
addtoeventtypelegend(index,-2,0,"covermode: "); // p2について、「covermode: 」というテキストを表示する
addtoeventtypelegend(index,2,1,"YellowToGreen"); // p2について、値が1なら数値の1ではなく「YellowToGreen」と表示される
addtoeventtypelegend(index,2,2,"RedToGreen"); // p2について、値が2なら数値の2ではなく「RedToGreen」と表示される
addtoeventtypelegend(index,3,0,""); // p3について、0を空白にする
addtoeventtypelegend(index,4,0,""); // p4について、0を空白にする
addtoeventtypelegend(index,-2,0,"covermode: "); // p2について、「covermode: 」というテキストを表示する
addtoeventtypelegend(index,2,1,"YellowToGreen"); // p2について、値が1なら数値の1ではなく「YellowToGreen」と表示される
addtoeventtypelegend(index,2,2,"RedToGreen"); // p2について、値が2なら数値の2ではなく「RedToGreen」と表示される
addtoeventtypelegend(index,3,0,""); // p3について、0を空白にする
addtoeventtypelegend(index,4,0,""); // p4について、0を空白にする
createevent (obj object, num time, num code[, str data, node involved])
説明
開発者向けです。このコマンドは、以後のモデルの実行中に発生するイベントを作成します。このイベントは、objectで指定されるオブジェクト用に作成されます。イベントは、このコマンドが呼び出されてからtime秒後に発生します。イベントが、作成されたのと同じシミュレーション時間で発生する必要がある場合、timeを0にします。イベントが発生すると、オブジェクトのクラスのOnTimerEventイベント関数が呼び出されます。この関数にはcode、data、involvedが渡されます。これらの値は、OnTimerEventでeventcode、eventdata、iとしてアクセスできます。一般に、作成または実行されたイベントのタイプを判定するにはeventcodeが使用されます。eventdataはイベントの説明で、ユーザーの利便性のため使用されます。通常、OnTimerEventの実行には重要でありません。イベントに関係するオブジェクト、たとえば進入や退出を行うフローアイテムなどはinvolvedとして渡され、OnTimerEventでiとして参照されます。コード用に次の値が定義済みで、ユーザーが使用できます。
1 - EVENT_OPENINPUTS
2 - EVENT_OPENOUTPUTS
3 - EVENT_PROCESSFINISH
4 - EVENT_CREATEPART
5 - EVENT_DESTROYPRODUCT
6 - EVENT_CONVEYEND
7 - EVENT_BEGINLOADTIME
8 - EVENT_BEGINUNLOADTIME
9 - EVENT_ENDLOADTIME
10 - EVENT_ENDUNLOADTIME
11 - EVENT_ENDDELAYTIME
12 - EVENT_BEGINDOWNTIME
13 - EVENT_ENDDOWNTIME
14 - EVENT_ENDWAITTIME
15 - EVENT_MEETBATCHQTY
16 - EVENT_ENDTRAVELTIME
17 - EVENT_ENDSETUP
ユーザーが独自のイベントタイプを作成する場合、100より大きな値をコードとして使用します。eventcodeとeventdataも参照してください。
1 - EVENT_OPENINPUTS
2 - EVENT_OPENOUTPUTS
3 - EVENT_PROCESSFINISH
4 - EVENT_CREATEPART
5 - EVENT_DESTROYPRODUCT
6 - EVENT_CONVEYEND
7 - EVENT_BEGINLOADTIME
8 - EVENT_BEGINUNLOADTIME
9 - EVENT_ENDLOADTIME
10 - EVENT_ENDUNLOADTIME
11 - EVENT_ENDDELAYTIME
12 - EVENT_BEGINDOWNTIME
13 - EVENT_ENDDOWNTIME
14 - EVENT_ENDWAITTIME
15 - EVENT_MEETBATCHQTY
16 - EVENT_ENDTRAVELTIME
17 - EVENT_ENDSETUP
ユーザーが独自のイベントタイプを作成する場合、100より大きな値をコードとして使用します。eventcodeとeventdataも参照してください。
例
if (current.subnodes.length >= current.mincontent)
{
createevent(current,5,EVENT_OPENOUTPUTS,"openoutputs",involved);
}
シミュレーションで5秒後に、currentのコンテンツがcurrentで参照されるオブジェクトのmincontentという名前のラベルより少なければ、currentとして指定されたオブジェクトの出力ポートを、involvedで指定されたフローアイテム用に開きます。
{
createevent(current,5,EVENT_OPENOUTPUTS,"openoutputs",involved);
}
シミュレーションで5秒後に、currentのコンテンツがcurrentで参照されるオブジェクトのmincontentという名前のラベルより少なければ、currentとして指定されたオブジェクトの出力ポートを、involvedで指定されたフローアイテム用に開きます。
createtickevent (obj fluidobject)
fluidobject、およびそのティッカーに割り当てられたすべてのオブジェクト用のティックイベントを作成する
説明
渡された流体オブジェクト、および同じティッカーでコントロールされる他のすべての流体オブジェクト用に、ティックイベントを作成します。これによりユーザーは、ティッカーの通常のティック時間とは異なる時間に流体物質を移動できます。ユーザーは、特定のティッカーをパラメータとしてこのコマンドに渡すこともできます。
例
createtickevent(current);
delayevents (num value)
説明
開発者向けです。eventlistのすべてのイベントを遅延させます。eventlistのすべてのイベントについて、時間がvalueだけ増やされます。
例
delayevents(20)
delayeventsofobject (obj object, num value)
説明
開発者向けです。オブジェクトのイベントを遅延させます。オブジェクトの時間付きイベントがvalueだけ増やされ、eventlistが並べ替えされます。valueには正と負のどちらも使用できます。
例
delayeventsofobject(model().subnodes[2],20)
destroyevent (node event)
説明
開発者向けです。イベントリストの特定のイベントを破棄します。
例
destroyevent(node("MAIN:/1/exec/events").last)
destroyeventsofobject (obj object [, num simtime, num code, str data, node involved])
オブジェクトに関連付けられているイベントを破棄する
説明
与えられたオブジェクトに関連付けらわれているイベントを破棄します。必須パラメータは、最初のパラメータobjectのみです。他のパラメータはオプションで、次に示すように、破棄するイベントを選択するフィルタとなります。
time:コマンドが呼び出された時間と等しいか、より大きければ、このパラメータはイベントを時間でフィルタリングします。イベントの時間が渡されたtimeと等しくなければ、イベントは破棄されません。フィルタとして使用しない場合、-1を渡します。
code:このパラメータが0より大きい場合、イベントコードでイベントをフィルタリングします。イベントのコードが渡されたcodeと等しくなければ、イベントは破棄されません。
data:NULL以外なら、このパラメータを使用し、イベントに関連付けられているデータ文字列でイベントがフィルタリングされます。イベントのデータ文字列が渡された文字列と等しくなければ、イベントは破棄されません。
involved:NULL以外なら、このパラメータにより、関係するノードやオブジェクトでイベントがフィルタリングされます。イベントの関連ノードが渡されたノードと等しくなければ、イベントは破棄されません。
time:コマンドが呼び出された時間と等しいか、より大きければ、このパラメータはイベントを時間でフィルタリングします。イベントの時間が渡されたtimeと等しくなければ、イベントは破棄されません。フィルタとして使用しない場合、-1を渡します。
code:このパラメータが0より大きい場合、イベントコードでイベントをフィルタリングします。イベントのコードが渡されたcodeと等しくなければ、イベントは破棄されません。
data:NULL以外なら、このパラメータを使用し、イベントに関連付けられているデータ文字列でイベントがフィルタリングされます。イベントのデータ文字列が渡された文字列と等しくなければ、イベントは破棄されません。
involved:NULL以外なら、このパラメータにより、関係するノードやオブジェクトでイベントがフィルタリングされます。イベントの関連ノードが渡されたノードと等しくなければ、イベントは破棄されません。
例
destroyeventsofobject(model().subnodes[2])
destroymessageevents (obj object, num time, obj fromobj[, num param1, num param2, num param3])
オブジェクトに関連付けらわれているメッセージイベントを破棄する
説明
与えられたオブジェクトに関連付けられているメッセージイベントを破棄します。
メッセージパラメータが含まれていなければ、すべてのメッセージイベントが破棄されます。
メッセージパラメータが含まれていなければ、すべてのメッセージイベントが破棄されます。
例
destroymessageevents(current, time(), NULL, 8)
eventcode <no parentheses>
説明
開発者向けです。このコマンドは、createevent()コマンドにコードとして渡された数値を返します。ライブラリオブジェクトのOnTimerEvent関数でのみ使用されます。通常は、発生しているイベントのタイプを識別するために使用されます。このコマンドを呼び出すときは括弧を付けません。createevent()とeventdataも参照してください。
例
if (eventcode == EVENT_OPENINPUTS)
thisobjectdata->openinputs();
createevent()関数にEVENT_OPENINPUTSという値が渡された場合、thisobjectdataで参照されるオブジェクトのopeninputs()というメソッドを呼び出します。
thisobjectdata->openinputs();
createevent()関数にEVENT_OPENINPUTSという値が渡された場合、thisobjectdataで参照されるオブジェクトのopeninputs()というメソッドを呼び出します。
eventdata <no parentheses>
説明
開発者向けです。このコマンドは、createevent()コマンドにデータとして渡された文字列値を返します。ライブラリオブジェクトのOnTimerEvent関数でのみ使用されます。通常は、発生しているイベントタイプのユーザー向け説明として使用されます。速度の理由から、OnTimerEvent関数の実行時には一般に使用されません。このコマンドを呼び出すときは括弧を付けません。createevent()とeventcodeも参照してください。
例
if (comparetext(eventdata,"openinputs"))
{
thisobjectdata->openinputs();
}
createevent()に渡された文字列値が「openinputs」と等しい場合、thisobjectdataで参照されるオブジェクトのopeninputsというメソッドを呼び出します。
{
thisobjectdata->openinputs();
}
createevent()に渡された文字列値が「openinputs」と等しい場合、thisobjectdataで参照されるオブジェクトのopeninputsというメソッドを呼び出します。
eventget (num index, num thing)
インデックスのイベントのイベント属性
説明
MAIN:/project/exec/eventsの指定されたインデックスにあるイベント属性を返します。
thingは次のいずれかです。
1 = クライアント
2 = 時間
3 = コード
4 = データ
5 = 関係
6 = イベントノード
thingは次のいずれかです。
1 = クライアント
2 = 時間
3 = コード
4 = データ
5 = 関係
6 = イベントノード
例
eventget(2,3)
eventloginfo (num operation, num n1)
説明
開発者向けです。イベントログに関係する何かを記述する文字列値を返します。
動作は次のいずれかです。
ELI_GET_OBJECTPATH 1 - objectpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_GET_INVOLVEDPATH 2 - involvedpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_GET_OTHERPATH 3 - objectpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_EVENTTYPE_NAME 4 - eventtypes配列から、インデックスn1にあるeventtypeの名前を返します。
ELI_LOGGEDEVENTTYPE_NAME 5 - loggedeventtypes配列から、インデックスn1にあるlogged eventtypeの名前を返します。
イベントログに関係し、数値を返す他のオペレーションには、applicationcommand()関数でアクセスできます。
「seteventlogging」- eventtype n1のログ記録を有効または無効にします。
「geteventlogging」- eventtype n1についてログ記録が有効かどうかを返します。
「getobjectpathslistsize」- objectpaths配列のサイズを返します。
「getinvolvedpathslistsize」- involvedpaths配列のサイズを返します。
「getotherpathslistsize」- objectpaths配列のサイズを返します。
「geteventtypeslistsize」- eventtypes配列のサイズを返します。
「getloggedeventtypeslistsize」- loggedeventtypes配列のサイズを返します。
「geteventtypecode」- n1として渡された名前のeventtypeのインデックスを返します。
動作は次のいずれかです。
ELI_GET_OBJECTPATH 1 - objectpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_GET_INVOLVEDPATH 2 - involvedpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_GET_OTHERPATH 3 - objectpaths配列から、インデックスn1にあるオブジェクトのパスを返します。
ELI_EVENTTYPE_NAME 4 - eventtypes配列から、インデックスn1にあるeventtypeの名前を返します。
ELI_LOGGEDEVENTTYPE_NAME 5 - loggedeventtypes配列から、インデックスn1にあるlogged eventtypeの名前を返します。
イベントログに関係し、数値を返す他のオペレーションには、applicationcommand()関数でアクセスできます。
「seteventlogging」- eventtype n1のログ記録を有効または無効にします。
「geteventlogging」- eventtype n1についてログ記録が有効かどうかを返します。
「getobjectpathslistsize」- objectpaths配列のサイズを返します。
「getinvolvedpathslistsize」- involvedpaths配列のサイズを返します。
「getotherpathslistsize」- objectpaths配列のサイズを返します。
「geteventtypeslistsize」- eventtypes配列のサイズを返します。
「getloggedeventtypeslistsize」- loggedeventtypes配列のサイズを返します。
「geteventtypecode」- n1として渡された名前のeventtypeのインデックスを返します。
例
string objectpath = eventloginfo(ELI_GET_OBJECTPATH,1);
eventqty ()
現在保留中のイベントの番号を取得する
説明
現在保留中のイベントの番号を返します。
例
eventqty()
listenerinfo (int info)
説明
開発者向けです。このコマンドは、OnListenおよびOnPreListenイベント関数内で使用するための情報を返します。
返される情報は、リッスンしているイベントに渡された情報です。
infoが1なら、エンジンイベントコードを返します。エンジンイベントコードには、SM_MESSAGEやSM_DRAWなどのマクロがあります。
infoが2および3なら、関連付けられているツリーノードへのポインターを返します。
リスニングを設定するには、リッスン先のオブジェクト(オブジェクトA)に「listeners」属性を追加します。listeners属性は、リッスン元のオブジェクト(オブジェクトB)に結合されているサブノードを持つ必要があります。オブジェクトAでイベントが起動する前に、オブジェクトBのOnPreListenイベント関数が起動します。オブジェクトAの最初のイベントの後、オブジェクトBのOnListenイベント関数が起動します。また、オブジェクトBの結合ノードの下に数値データを持つサブノードを追加し、イベントをフィルタリングすることもできます。数値データには、リッスンするビットシフトされたイベントコードの、ビット単位の合計を使用します。結合にサブノードがない場合、オブジェクトはデフォルトですべてのイベントをリッスンします。
返される情報は、リッスンしているイベントに渡された情報です。
infoが1なら、エンジンイベントコードを返します。エンジンイベントコードには、SM_MESSAGEやSM_DRAWなどのマクロがあります。
infoが2および3なら、関連付けられているツリーノードへのポインターを返します。
リスニングを設定するには、リッスン先のオブジェクト(オブジェクトA)に「listeners」属性を追加します。listeners属性は、リッスン元のオブジェクト(オブジェクトB)に結合されているサブノードを持つ必要があります。オブジェクトAでイベントが起動する前に、オブジェクトBのOnPreListenイベント関数が起動します。オブジェクトAの最初のイベントの後、オブジェクトBのOnListenイベント関数が起動します。また、オブジェクトBの結合ノードの下に数値データを持つサブノードを追加し、イベントをフィルタリングすることもできます。数値データには、リッスンするビットシフトされたイベントコードの、ビット単位の合計を使用します。結合にサブノードがない場合、オブジェクトはデフォルトですべてのイベントをリッスンします。
例
treenode current = c;
treenode involved = i;
int code = listenerinfo(1);
treenode associated = tonode(listenerinfo(2));
treenode coupling = tonode(listenerinfo(3));
print("OnListen");
print("current: ", current);
print("involved: ", involved);
print("code: ", code);
print("associated: ", associated);
print("coupling: ", coupling); logevent (num/str index/name[, obj object, obj involved, num p1, num p2, num p3, num p4])
説明
イベントログのエントリとしてイベントをログ記録します。registereventtype()に渡された名前、またはregistereventtype()により返されたインデックスが使用されます。
例
logevent("MyEventType",current,item,port);
registereventtype (str name)
説明
イベントログで使用するカスタムイベントタイプを登録します。eventtypeのインデックスが返され、このインデックスは後でlogevent()など他のコマンドで使用できます。
例
int index = registereventtype("MyEventType");
startlisten (obj listener)
説明
開発者向けです。実行ファイルに対して、オブジェクトがリスナーであることを通知します。これはセッション間で継続されません。このコマンドは、実行ファイルのリスナーリストに、リスナーをポイントするノードを追加します。セッションが再ロードされるか、コンパイル後には、リスナーをリセットする必要があります。リスニングメカニズムは実行ファイルに大きな負荷をかける可能性があるため、使用は最小限にしてください。リスナーは、モデルのいずれかのオブジェクトにイベント(OnTimerEvent)がディスパッチされたとき、OnListenメッセージを受け取ります。リスナーはメッセージをフィルタリングし、OnListenメッセージに応答するかどうかを決定する必要があります。OnListenメッセージに渡されるパラメータについては、「オンラインリファレンスガイド」を参照してください。
例
startlisten(so())
stoplisten (obj listener)
説明
開発者向けです。実行ファイルに対して、このオブジェクトがリスナーでなくなったことを通知します。このコマンドは、リスナーへのポインターが以前にstartlisten()コマンドでリスナーリストに追加されていれば、リストからポインターを削除します。リスナーは、モデルのいずれかのオブジェクトにイベント(OnTimerEvent)がディスパッチされたとき、OnListenメッセージを受け取ります。
例
stoplisten(so())
FixedResources
FixedResourceオブジェクトに関連付けられているコマンド。これらのコマンドのほとんどは、BasicConveyorまたはBasicFRオブジェクトのカスタム動作を開発するとき使用されます。
evaluatepullcriteria (obj fixedresource, obj item, num portnr[, num bypassflags])
FixedResourceオブジェクトのプル要件を再起動する
説明
FixedResourceに対して、入力ポートportnr経由で渡されたオブジェクトのアイテムのプル要件を評価するよう通知します。このコマンドは、アイテムがプル可能な場合、プル要件のフィールドにより返される値を返します。理由にかかわらずアイテムをプルできない場合(ポートが閉じている、アイテムがリリースされていないなど)、このコマンドは0を返します。bypassflagsパラメータは、BYPASS_で始まるマクロのビット単位の組み合わせで、アイテムが利用可能かどうかを判定するときに特定の基準を無視するよう指定します。
例
evaluatepullcriteria(current, item, 1); // [ベストアイテムからプル]ピックリストオプションも参照
getiteminvolved (obj item)
アイテムのFixedResource関連の変数に保存されているオブジェクト参照を取得する
説明
アイテムのFixedResource関連の変数に保存されているオブジェクト参照を返します。
FixedResourceクラスでは、各フローアイテムに関連する1つの変数をサブクラスに保存できます。これらの変数の意味は、クラスのタイプによって異なります。
たとえば、プロセッサがプロセスまたは設定時間にオペレーターを使用するよう設定されている場合、プロセッサは関連変数を使用して、フローアイテム用に呼び出されるディスパッチャーへの参照を保存します。
モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをsetitemvar、getitemvar、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
FixedResourceクラスでは、各フローアイテムに関連する1つの変数をサブクラスに保存できます。これらの変数の意味は、クラスのタイプによって異なります。
たとえば、プロセッサがプロセスまたは設定時間にオペレーターを使用するよう設定されている場合、プロセッサは関連変数を使用して、フローアイテム用に呼び出されるディスパッチャーへの参照を保存します。
モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをsetitemvar、getitemvar、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
例
getiteminvolved(current.first)
getitemsendto (obj item)
アイテムについて評価されたsendtoの値を取得する
説明
itemがFixedResource内に存在し、リリースされていれば、そのアイテムについて評価されたsendtoの値を返します。
例
getitemsendto(item)
getitemstate (obj item)
フローアイテムのFixedResource状態を取得する
説明
フローアイテムのFixedResource状態を返します。これは、次に示す3つの値のいずれかです。
FRSTATE_INQUEUE:フローアイテムは処理中で、まだリリースされていません。
FRSTATE_READY:フローアイテムはリリース済みですが、それを受け取る準備の整った下流オブジェクトが見つかっていません。
FRSTATE_MOVEREQUESTED:フローアイテムはリリース済みで、下流オブジェクトの受け取り準備が整っていますが、アイテムは輸送によるピックアップ待ちです。
詳細については、FixedResourceのドキュメントを参照してください。
FRSTATE_INQUEUE:フローアイテムは処理中で、まだリリースされていません。
FRSTATE_READY:フローアイテムはリリース済みですが、それを受け取る準備の整った下流オブジェクトが見つかっていません。
FRSTATE_MOVEREQUESTED:フローアイテムはリリース済みで、下流オブジェクトの受け取り準備が整っていますが、アイテムは輸送によるピックアップ待ちです。
詳細については、FixedResourceのドキュメントを参照してください。
例
getitemstate(so())
getitemvar (obj item, num var)
アイテム用のFixedResource変数の値を取得する
説明
アイテム用のFixedResource変数の値を返します。varパラメータは1、2、3のいずれかです。FixedResourceクラスでは、各フローアイテムについて3つの数値変数をサブクラスに保存できます。これらの変数の意味は、クラスのタイプによって異なります。
たとえば、プロセッサは変数1にアイテムの処理開始時間を、変数2にアイテムの処理時間を保存できます。
モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをsetitemvar、getiteminvolved、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
たとえば、プロセッサは変数1にアイテムの処理開始時間を、変数2にアイテムの処理時間を保存できます。
モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをsetitemvar、getiteminvolved、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
例
getitemvar(current.first, 3)
holditem (obj item)
アイテムがリリース済みなら保持する
説明
指定されたアイテムがリリース済みなら、それを保持します。このコマンドは実質的にアイテムを「リリース取り消し」し、退出を防止します。アイテムがFixedResource内に存在し、リリース済みで、下流オブジェクトに「割り当て」されていない(輸送待ちでない)場合のみ適用されます。
例
holditem(item)
inititem (obj item)
フローアイテムのFixedResource変数を初期化する
説明
フローアイテムのFixedResource変数を初期化します。通常は、フローアイテムが初めて固定リソースに進入したときに行われます。この動作は通常は自動的に行われますが、独自のBasicFRオブジェクト動作を開発するとき、例外的なケースで使用できます。
例
inititem(item)
pullitem (obj fixedresource, obj item, num portnr[, num bypassflags])
説明
fixedresourceに対して、入力ポートportnr経由で渡されたオブジェクトのアイテムのプル要件を評価するよう通知します。プル評価が真なら、このコマンドはただちにアイテムをプルします。このコマンドは、アイテムが正常にプルされれば1を、そうでなければ0を返します。理由にかかわらずアイテムをプルできない場合(ポートが閉じている、アイテムがリリースされていないなど)、このコマンドは0を返します。bypassflagsパラメータは、BYPASS_で始まるマクロのビット単位の組み合わせで、アイテムが利用可能かどうかを判定するときに特定の基準を無視するよう指定します。BYPASS_ALLを指定すると、利用可能性にかかわらずただちにアイテムがプルされます。
例
pullitem(current, item, 1); // [ベストアイテムからプル]ピックリストオプションも参照
receiveitem (obj station [, num port ] )
FixedResourceに対して、入力を開きフローアイテムを受け付けるよう通知する
説明
FixedResourceステーションに対して、入力を開きフローアイテムを受け付けるよう通知します。
portパラメータはオプションで、どのポートから受信すべきかが正確に判明している場合のみ使用します。portパラメータが指定されている場合、このオブジェクトは上流オブジェクトの対応する出力ポートが開いていれば、そのオブジェクトからアイテムの受け付けを試み、アイテムの以前のsend-to戻り値を無視します(プルロジックの動作と同様です)。この関数は、アイテムを受け付けるため1回、アイテムの受け付け後に(または受け付けの確認後に)1回だけ実行します。
releaseitem()コマンドも参照してください。この関数は、BasicFRまたはBasicConveyorのコードフィールド内でのみ使用します。他のオブジェクトには独自のreceiveitem()が実装されています。
portパラメータはオプションで、どのポートから受信すべきかが正確に判明している場合のみ使用します。portパラメータが指定されている場合、このオブジェクトは上流オブジェクトの対応する出力ポートが開いていれば、そのオブジェクトからアイテムの受け付けを試み、アイテムの以前のsend-to戻り値を無視します(プルロジックの動作と同様です)。この関数は、アイテムを受け付けるため1回、アイテムの受け付け後に(または受け付けの確認後に)1回だけ実行します。
releaseitem()コマンドも参照してください。この関数は、BasicFRまたはBasicConveyorのコードフィールド内でのみ使用します。他のオブジェクトには独自のreceiveitem()が実装されています。
例
receiveitem(current)
recycleitem (obj item , num binrank )
フローアイテムをflowItem binにリサイクルする
説明
指定されたフローアイテムをflowitem binにリサイクルします。binrankは、flowitem binをリサイクルする先のランクです(texturedcoloredbox = 5など)。
例
recycleitem(item, 5);
releaseitem (obj flowitem [, num port ])
フローアイテムを現在のオブジェクトからリリースする
説明
指定されたフローアイテムをリリースします。フローアイテムは、現在そのアイテムが含まれているオブジェクトから自由に退出可能な時にリリースされ、その時点で[ポートに送信]が評価されます。このコマンドは、フローアイテムがBasicFRオブジェクト内にあり、フローアイテムがまだリリースされていない、またはいずれかのFixedResourceでholditem()により保持されている場合のみ使用します。
2番目のパラメータportはオプションです。このパラメータが渡された場合、sendtoは評価されず、アイテムは指定のポートからリリースされます。フローアイテムが存在する場合、releaseitemは1を返します。それ以外の場合、0を返します。
receiveitem()コマンドも参照してください。
2番目のパラメータportはオプションです。このパラメータが渡された場合、sendtoは評価されず、アイテムは指定のポートからリリースされます。フローアイテムが存在する場合、releaseitemは1を返します。それ以外の場合、0を返します。
receiveitem()コマンドも参照してください。
例
releaseitem(item)
resetuniqueid (obj flowitem)
フローアイテムのuniqueid属性を、他のフローアイテムに割り当てられていない値にリセットします。
説明
このコマンドは、フローアイテムのuniqueid属性を、他のフローアイテムに既に割り当てられていない値にリセットします。この属性は、フルレポート用の全履歴情報を収集するために必要です。このコマンドは、フローアイテムが破棄されていないが、データ取集上の目的から新規アイテムと見なす必要がある場合に使用します。たとえば、フローアイテムがモデラーによりリサイクルされる(内蔵のリサイクリング機能を使用せず)場合、フローアイテムが循環に戻されたときにこのコマンドを呼び出します。フローアイテムは通常、全履歴収集が有効なときのみuniqueid属性を持ちます。
例
resetuniqueid(item);
resumetransportsin (obj fixedresource [, num saverank])
説明
BasicFRオブジェクトのトリガーからのみ実行し、通常は[オブジェクトを再開]フィールドからのみ実行します。このコマンドは、savestoppedtransportinコマンドを使用して保存されたtaskexecutersへの参照を探し、アンロード操作を再開できることをtaskexecutersに通知します。saverankパラメータは、特定の保存済み参照のツリー内でのランクを指します。saverankパラメータが指定されていない場合、すべての保存済み参照が再開されます。このパラメータが指定されている場合、指定されたランクに関連付けられているtaskexecuterのみが再開を許可されます。保存済み参照は、BasicFRのnroftransportsin変数のサブノードとして格納されます。特定の保存済みtaskexecutersへの参照は、nroftransportsinnode.subnodes[saverank].valueで参照できます。
例
resumetransportsin(current);
resumetransportsout (obj fixedresource [, num saverank])
説明
BasicFRオブジェクトのトリガーからのみ実行し、通常は[オブジェクトを再開]フィールドからのみ実行します。このコマンドは、savestoppedtransportoutコマンドを使用して保存されたtaskexecutersへの参照を探し、ロード操作を再開できることをtaskexecutersに通知します。saverankパラメータは、特定の保存済み参照のツリー内でのランクを指します。saverankパラメータが指定されていない場合、すべての保存済み参照が再開されます。このパラメータが指定されている場合、指定されたランクに関連付けられているtaskexecuterのみが再開を許可されます。保存済み参照は、BasicFRのnroftransportsout変数のサブノードとして格納されます。特定の保存済みtaskexecutersへの参照は、nroftransportsoutnode.subnodes[saverank].valueで参照できます。
例
resumetransportsout(current);
savestoppedtransportin (obj fixedresource, obj taskexecuter)
説明
BasicFRオブジェクトの完全なトリガーの輸送からのみ実行します。
taskexecuterがアンロードしようとしているアイテムについて、BasicFRで受け付け準備が整っていない場合、BasicFRはtaskexecuterへの参照を保存してから値-1を返す必要があります。
その後でtaskexecuterはブロック状態に移行し、BasicFRで受け付け準備が整うまで待ちます。BasicFRは、アイテムの受け付け準備が整ったときresumetransportsin()コマンドを呼び出します。
これにより保存済みの参照が調べられ、対応するtaskexecutersに対して、アンロードオペレーションをすぐに再開可能であると通知されます。
taskexecuterがアンロードしようとしているアイテムについて、BasicFRで受け付け準備が整っていない場合、BasicFRはtaskexecuterへの参照を保存してから値-1を返す必要があります。
その後でtaskexecuterはブロック状態に移行し、BasicFRで受け付け準備が整うまで待ちます。BasicFRは、アイテムの受け付け準備が整ったときresumetransportsin()コマンドを呼び出します。
これにより保存済みの参照が調べられ、対応するtaskexecutersに対して、アンロードオペレーションをすぐに再開可能であると通知されます。
例
if(getvarnum(current, "nrofstops") > 0)
{
savestoppedtransportin(current, transporter);
return -1;
}
{
savestoppedtransportin(current, transporter);
return -1;
}
savestoppedtransportout (obj fixedresource, obj taskexecuter)
説明
BasicFRオブジェクトから外への完全なトリガー輸送からのみ実行します。
taskexecuterがロードしようとしているアイテムについて、BasicFRで送る準備が整っていない場合、BasicFRはtaskexecuterへの参照を保存してから値-1を返す必要があります。
その後でtaskexecuterはブロック状態に移行し、BasicFRで送出準備が整うまで待ちます。BasicFRは、アイテムの送出準備が整ったときresumetransportsoutコマンドを呼び出します。
これにより保存済みの参照が調べられ、対応するtaskexecutersに対して、ロードオペレーションをすぐに再開可能であると通知されます。
taskexecuterがロードしようとしているアイテムについて、BasicFRで送る準備が整っていない場合、BasicFRはtaskexecuterへの参照を保存してから値-1を返す必要があります。
その後でtaskexecuterはブロック状態に移行し、BasicFRで送出準備が整うまで待ちます。BasicFRは、アイテムの送出準備が整ったときresumetransportsoutコマンドを呼び出します。
これにより保存済みの参照が調べられ、対応するtaskexecutersに対して、ロードオペレーションをすぐに再開可能であると通知されます。
例
if(getvarnum(current, "nrofstops") > 0)
{
savestoppedtransportout(current, transporter);
return -1;
}
{
savestoppedtransportout(current, transporter);
return -1;
}
setiteminvolved (obj item, obj involved)
説明
アイテムのFixedResource関連の変数に保存されているオブジェクト参照を設定します。FixedResourceクラスでは、各フローアイテムに関連する1つの変数をサブクラスに保存できます。これらの変数の意味は、クラスのタイプによって異なります。たとえば、プロセッサがプロセスまたは設定時間にオペレーターを使用するよう設定されている場合、プロセッサは関連変数を使用して、フローアイテム用に呼び出されるディスパッチャーへの参照を保存します。このコマンドは、モデルで明示的なFixedResourceクラスをandオブジェクトとして使う場合のみ使用します。このコマンドとsetitemvar、getitemvar、getiteminvolvedコマンドを併用して、オブジェクトが受け付けるアイテムに変数を保存できます。
例
setiteminvolved(current.first, current.centerObjects[1])
setitemsendto (obj item, num value)
説明
アイテムがFixedResource内に存在するなら、そのアイテムのsendtoの値を設定します。このコマンドは、明示的なFixedResourceクラスのオブジェクトを使用しており、アイテムをリリースする前にsendto値を保存し、後でreleaseitem()コマンドを使用してポートを渡すときのみ使用します。リリース済みのアイテムの評価済みsendtoを変更する場合は、このコマンドを使用する代わりに、holditem()を実行してからreleaseitem()を再実行してください。
例
setitemsendto(item, current.currentsendto)
setitemvar (obj item, num var, num value)
説明
アイテム用のFixedResource変数の値を設定します。varパラメータは1、2、3のいずれかで、valueパラメータには設定する値を指定します。FixedResourceクラスでは、各フローアイテムについて3つの数値変数をサブクラスに保存できます。これらの変数の意味は、クラスのタイプによって異なります。
たとえば、プロセッサは変数1にアイテムの処理開始時間を、変数2にアイテムの処理時間を保存できます。モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをgetitemvar、getiteminvolved、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
たとえば、プロセッサは変数1にアイテムの処理開始時間を、変数2にアイテムの処理時間を保存できます。モデルのオブジェクトとして明示的なFixedResourceクラスを使用している場合、このコマンドをgetitemvar、getiteminvolved、setiteminvolvedコマンドとともに使用して、オブジェクトが受け取るアイテムの変数を保存できます。
例
setitemvar(current.first, 3, time())
transportincomplete (obj object, obj item [, num inport, obj transporter])
FixedResourceオブジェクトに、アイテムが運び込まれることを通知する
説明
このコマンドは、下流のFixedResourceオブジェクトに対して、指定されたアイテムが上流のオブジェクトから運び込まれることを通知します。このコマンドは、上流オブジェクトの[輸送を使用]フィールドがチェックされており、FRLOADタスクを使用する代わりにアイテムを明示的に移動する場合のみ使用します。これにより下流のFixedResourceは、オブジェクトに進入することが予定されているが、まだ到着していないアイテムがいくつ存在するかのデータを管理できます。このコマンドは、moveobjectコマンドでアイテムを移動する直前に実行します。詳細については、FixedResourceのドキュメントを参照してください。このコマンドが0を返した場合、オブジェクトはstopobjectコマンドで停止されており、アイテムを運び込むにはアイテムが再開されるまで待つ必要があります。
例
transportincomplete(current.outObjects[port], item, opipno(current, port));
この例は、輸送を使用せずフローアイテムをただちに移動するとき、moveobjectコマンドの前に[輸送の要求元]フィールドから実行します。
この例は、輸送を使用せずフローアイテムをただちに移動するとき、moveobjectコマンドの前に[輸送の要求元]フィールドから実行します。
transportoutcomplete (obj object, obj item [, num outport, obj transporter])
FixedResourceオブジェクトに、アイテムが運び出されることを通知する
説明
このコマンドは、FixedResourceオブジェクトに対して、指定されたアイテムが運び出されることを通知します。このコマンドは、オブジェクトの[輸送を使用]フィールドがチェックされており、FRLOADタスクを使用する代わりにアイテムを明示的に移動する場合のみ使用します。これによりFixedResourceは、オブジェクトから退出する準備が整っているが、まだオブジェクトに存在するアイテムがいくつ存在するかのデータを管理できます。このコマンドは、moveobjectコマンドでアイテムを移動する直前に実行します。詳細については、FixedResourceのドキュメントを参照してください。このコマンドが0を返した場合、オブジェクトはstopobjectコマンドで停止されており、アイテムを運び込むにはアイテムが再開されるまで待つ必要があります。
例
transportoutcomplete(current, item, port);
この例は、輸送を使用せずフローアイテムをただちに移動するとき、moveobjectコマンドの前に[輸送の要求元]フィールドから実行します。
この例は、輸送を使用せずフローアイテムをただちに移動するとき、moveobjectコマンドの前に[輸送の要求元]フィールドから実行します。
キネマティクスとスプライン
キネマティクスとスプラインの数学演算に関連するコマンド。
addkinematic (node infonode, num x, num y, num z, num targetspeed, num acc, num dec, num startspeed, num endspeed, num starttime, num type )
キネマティクスの組に1つのキネマティクス演算を追加する
説明
キネマティクスの組に1つのキネマティクス演算を追加します。詳細については、キネマティクスのユーザーマニュアルのドキュメントを参照してください。
例
addkinematic(current.labels["kinematics"], 1, 0, 0, 5,0,0, 0,0, time(), KINEMATIC_TRAVEL);
deactivatekinematics (node kinematicsnode)
updatekinematics()が呼び出されたときキネマティクスが何も行わないようにする
説明
以後にupdatekinematics()が呼び出されたとき、キネマティクスがオブジェクトを更新する代わりに、何も行わないようにします。オブジェクトのリセットトリガーでこのコマンドを呼び出すと、オブジェクトは正投影ビューで自由に移動できるようになります。
例
deactivatekinematics(current.labels["kinLabel"]);
dynamicsplineall (node starttree)
説明
開発者向けです。starttreeの下のオブジェクトについて、すべてのスプラインをキャッシュから消去します。モデル内のスプラインはすべて、編集可能または「ロック解除」になります。編集可能モードでは、スプラインのレンダリングが遅くなります。編集可能モードでは、スプラインを動的に編集できます。
例
dynamicsplineall(model())
fastspline (obj spline, num perc [0-1])
説明
開発者向けです。キャッシュされているスプラインからスプラインマッピングを取得します。このコマンドは、以後のsplinex()、spliney()、splinez()、splinerx()、splinery()、splinerz()、splinelength()、splineposobject()コマンドへの呼び出しにより返される値を設定します。splineで与えられるスプラインオブジェクトについて、事前に計算された値を使用します。パラメータpercは、対象のスプラインに沿った場所です。事前に計算された値は、fastsplineall()またはfastsplineupdate()コマンドが使用されたとき評価されます。
例
fastspline(splinestartnode,1)
最も離れたポイント(スプラインに沿って100%)でsplinestartnodeを指すスプラインをアクティブにします。
最も離れたポイント(スプラインに沿って100%)でsplinestartnodeを指すスプラインをアクティブにします。
fastsplineall (obj starttree {model}, num res)
説明
開発者向けです。すべてのスプラインを同時にキャッシュします。スプラインジオメトリのレンダリングと評価を高速化するため、モデルのすべてのスプラインについて、ジオメトリが評価され「ロック」されます。このコマンドは、fastspline()を呼び出したとき、以後のsplinex()、spliney()、splinez()、splinery()、splinery()、splinery()、splinelength()、splineposobject()コマンドへの呼び出しにより返される値を設定します。
例
fastsplineall(model(),20)
fastsplineupdate (obj spline, num res)
説明
開発者向けです。高速化のため、スプラインの形状をキャッシュします。スプラインジオメトリのレンダリングと評価を高速化するため、モデルのすべてのスプラインについて、ジオメトリが再評価され「ロック」されます。このコマンドは、fastspline()を呼び出したとき、以後のsplinex()、spliney()、splinez()、splinery()、splinery()、splinery()、splinelength()、splineposobject()コマンドへの呼び出しにより返される値を設定します。
例
fastsplineupdate(so(),20)
getkinematics (node infonode, num querytype[, num kinematicindex, num updatetime/traveldist])
指定されたキネマティクス演算から情報を取得する
説明
指定されたキネマティクス演算から情報を取得します。詳細については、キネマティクスのヘルプドキュメントを参照してください。
例
getkinematics(current.labels["kinematics"], KINEMATIC_ARRIVALTIME, 1, current.size.x);
initkinematics (node infonode, obj/num object/x[, num flags/y, num z, num rx, num ry, num rz, num flags, num unused])
キネマティクス演算を初期化する
説明
キネマティクス演算を初期化します。
infonodeは、キネマティクス情報を保持できる空白のノードです。
objectは、キネマティクスを実行する対象のオブジェクトです。
flagsは、動作を定義する各種のフラグです。
unusedパラメータは廃止されました。これはflagsパラメータで定義できます。
詳細については、ユーザーマニュアルにあるキネマティクスのドキュメントを参照してください。
infonodeは、キネマティクス情報を保持できる空白のノードです。
objectは、キネマティクスを実行する対象のオブジェクトです。
flagsは、動作を定義する各種のフラグです。
unusedパラメータは廃止されました。これはflagsパラメータで定義できます。
詳細については、ユーザーマニュアルにあるキネマティクスのドキュメントを参照してください。
例
initkinematics(current.labels["kinematics"], current)
profilekinematics (node infonode, num kinematicindex)
指定されたキネマティクス演算についての情報を出力コンソールに表示する
説明
指定されたキネマティクス演算についての情報を出力コンソールに表示します。詳細については、キネマティクスのヘルプドキュメントを参照してください。
例
printkinematics(current.labels["kinematics"], 0);
scalekinematicstotime (node kinematics, int kinematicnr, double scaletotime)
キネマティクスを定義した時間にスケーリングする
説明
キネマティクスを定義した時間にスケーリングします。このコマンドを使用して、キネマティクスの特性(加速->ピーク速度->減速)を保持しながら、キネマティクスの実行に要する合計時間を、分布など他のメカニズムで定義できます。kinematicnrが0なら、キネマティクスの組の全体が、与えられた時間にスケーリングされます。Kinematicnrが0より大きければ、そのキネマティクスのみがスケーリングされます。戻り値は、キネマティクスの新しい終了時間です。
例
scalekinematicstotime(kinematics, 0, exponential(0, 10));
setkinematicsrotoffset (node infonode, num rx, num ry, num rz)
説明
キネマティクス演算の最初のキネマティクス回転オフセットを設定します。詳細については、キネマティクスのヘルプドキュメントを参照してください。
例
setkinematicsrotoffset(current.labels["kinematics"], 0, 0, 180);
spline (obj spline, num perc)
説明
開発者向けです。スプラインマッピングを計算し、スプラインオブジェクトsplineを使用して、現在のスプラインパラメータを設定します。このコマンドは、以後のsplinex()、spliney()、splinez()、splinerx()、splinery()、splinerz()、splinelength()、splineposobject()コマンドへの呼び出しにより返される値を設定します。fastspline()とは異なり、splineで与えられたスプラインオブジェクトの事前に計算された値を設定しません。パラメータpercは、対象のスプラインに沿った場所です。このコマンドは、fastsplineall()やfastsplineupdate()コマンドが使用されたときのように、事前に計算された値をロックしません。スプラインは、出力ポートから入力ポートに接続された、オブジェクトの任意のチェーンとして定義できます。出力ポートから入力ポートへのチェーンで最初のオブジェクトを、パラメータ1として渡します。
例
spline(splinestartobject,0.6)
splinedraw (obj object)
説明
開発者向けです。spline()で計算された現在のスプラインジオメトリに基づいて、スプラインに沿ったラインを描画します。
例
splinedraw()
splinedrawextrusion (obj object, num step, num wide, num high, num top, num side)
説明
開発者向けです。長方形の押し出し付きのspline()で計算された現在のスプラインジオメトリに基づいて、スプラインを描画します。スプラインオブジェクトのパラメータを使用します。
例
splinedrawextrusion(current,20,1,2,1,1)
splinelength ()
説明
開発者向けです。現在のスプラインのパラメータ。現在のスプラインの長さを返します。
例
splinelength()
splineposobject (obj object)
説明
開発者向けです。現在のスプラインのパラメータに従ってオブジェクトを配置します。
例
splineposobject(current)
splinerx ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上にオブジェクトが配置された場合の、オブジェクトの方向を返します。
例
splinerx()
splinery ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上にオブジェクトが配置された場合の、オブジェクトの方向を返します。
例
splinery()
splinerz ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上にオブジェクトが配置された場合の、オブジェクトの方向を返します。
例
splinerz()
splinex ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上の位置を返します。
例
splinex()
spliney ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上の位置を返します。
例
spliney()
splinez ()
説明
開発者向けです。現在のスプラインのパラメータ。spline()への最後の呼び出しで与えられたパラメータpのスプライン上の位置を返します。
例
splinez()
updatekinematics (node infonode, obj object [, num updatetime])
オブジェクトのキネマティクスに基づいて、オブジェクトの場所を更新する
説明
キネマティクス演算と現在の時間に基づいて、オブジェクトの場所を更新します。詳細については、キネマティクスのヘルプドキュメントを参照してください。
例
updatekinematics(current.labels["kinematics"], current, time());
言語
FlexscriptまたはC++のキーワードと構造体。
a <括弧なし>
説明
このコマンドは、forobjectlayerunder()やforobjecttreeunder()など特定のflexscriptコマンドの繰り返しにおいて、オブジェクトを参照するため使用されます。このコマンドには括弧は必要なく、C++でのみ使用できます。
例
forobjecttreeunder()を参照してください。
break
説明
switchステートメント{}のループまたはcaseを抜け出す
例
break;
case value:
説明
switchステートメント{}のcaseの1つ。
例
case 5: { msg("case statement",""); }
continue
説明
forまたはwhileループについて、現在のループにおける残りのコードを実行せず、ただちに次の繰り返しに移行します。
例
if(thisloopnotneeded) continue;
default :
説明
switchステートメントのデフォルトのcase。
例
default: { msg("case statement",""); }
else { }
説明
「if」ステートメントと組み合わせて使用され、「if」の条件が偽のときに実行すべきコードを(存在するなら)宣言します。
例
if( item.Weight < 100 )
{
msg("TRUE","");
}
else
{
msg("FALSE","");
}
この例は、アイテムのWeightラベルの値が100よりも小さい場合はTRUEのメッセージを、それ以外の場合はFALSEのメッセージを表示します。
{
msg("TRUE","");
}
else
{
msg("FALSE","");
}
この例は、アイテムのWeightラベルの値が100よりも小さい場合はTRUEのメッセージを、それ以外の場合はFALSEのメッセージを表示します。
for (initalstatement; whiletrueexpression ; countstatement)
説明
多くの回数のループを実行します。initialstatementは、ループの開始前に1回実行されます。whiletrueexpressionは各ループの実行前に評価され、この式が真になるとループは停止します。countstatementは各ループの終了時に実行され、通常はカウンターを増やします。詳細については、「FlexSimでロジックを記述する」の下にあるヘルプマニュアルを参照してください。
例
for(int i = 1; i <= 5; i++)
{
msg("for loop","");
}
{
msg("for loop","");
}
forobjecttreeunder (node container) { }
説明
ツリー内でコンテナとして指定されたノードの下にある各ノードのコードブロックを実行します。サブツリーもすべて含まれます。ループ内で現在アクティブなノードにアクセスするため、「a」コマンドが使用されます。forobjecttreeunder()コマンドはflexscriptでのみ使用でき、C++では使用できません。
例
forobjecttreeunder(model())
{
pt(a.name); pr();
}
モデル内のすべてのオブジェクト(他のオブジェクト内にあるものも含む)の名前を出力コンソールに表示します。
{
pt(a.name); pr();
}
モデル内のすべてのオブジェクト(他のオブジェクト内にあるものも含む)の名前を出力コンソールに表示します。
if (num condition) { }
説明
条件が真(条件式が1を返す)なら、閉じ括弧の直後にあるステートメントが実行されます。閉じ括弧の直後にあるのがブレース({ })なら、条件が真のとき、ブレース内のコードブロックが実行されます。条件が偽(0を返す)なら、「else」が定義されていない限りは何も実行されません。詳細については、ユーザーマニュアルを参照してください。
例
if (item.Weight < 100)
msg("TRUE", "");
この例は、アイテムのWeightラベルの値が100より小さければ、「TRUE」というポップアップメッセージを表示します。
msg("TRUE", "");
この例は、アイテムのWeightラベルの値が100より小さければ、「TRUE」というポップアップメッセージを表示します。
return (num value)
説明
このコマンドは関数の実行を停止し、その関数を呼び出した元の関数に値を戻します。
例
double res = item.rank * 5;
return res;
itemにより参照されるアイテムのランクを5倍した値をresに設定します。その後で、resに格納されている値が、この関数を呼び出した元の関数に返されます。
return res;
itemにより参照されるアイテムのランクを5倍した値をresに設定します。その後で、resに格納されている値が、この関数を呼び出した元の関数に返されます。
stringcompare (str text1, str text2)
文字列をアルファベット順に比較する
説明
文字列をアルファベット順に比較します。文字列が同一のものなら、戻り値は0です。text1がアルファベット順でtext2より前なら、負の数値が返されます。text1がアルファベット順でtext2より後なら、正の数値が返されます。C++のstrcmp()関数と同じものです。
例
stringcompare("zenith","beta")は1を返します。
comparetext("aqua","yellow")は-1を返します。
comparetext("aqua","yellow")は-1を返します。
switch (num value)
説明
valueに基づいて、いくつかの可能なcaseのいずれかを実行します。
例
int msgcase = msgparam(1);
switch(msgcase)
{
case 1:msg("","case 1");break;
case 2:msg("","case 2");break;
default:msg("","case 2");break;
}
switch(msgcase)
{
case 1:msg("","case 1");break;
case 2:msg("","case 2");break;
default:msg("","case 2");break;
}
while (num expression) {}
説明
expressionが0以外の値を返す間、次のブロック{}を繰り返し実行します。値が決して偽にならない場合、FlexSimがフリーズする可能性があるため、この関数の使用には注意してください。
例
while(current.subnodes.length > 4)
{
current.last.destroy();
}
{
current.last.destroy();
}
メディア
画像、サウンド、3D形状、動画、フライパスなど、プレゼンテーションとメディアに関連付けられているコマンド。
applyshapefactors (obj object)
すべての形状係数をオブジェクトに適用する
説明
このコマンドは、オブジェクトに形状係数が存在すれば、そのオブジェクトにすべての形状係数を適用します。
例
applyshapefactors(item);
autoloadallmedia ([node thenode])
説明
開発者向けです。このコマンドは、現在のビュー、ライブラリ、モデルに必要なすべてのメディア(画像と形状)をロードします。画像は.bmpまたは.jpgグラフィックスファイルです。形状は.3dsまたは.wrlファイルです。このコマンドは、多くの画像や形状をロードする必要があると、完了に多少の時間を要することがあります。このコマンドは、C++では使用できません。
例
autoloadallmedia();
現在のモデルに必要なすべてのメディアを再ロードします。
現在のモデルに必要なすべてのメディアを再ロードします。
autoloadimages ()
説明
開発者向けです。このコマンドは、現在のビュー、ライブラリ、モデルに必要なすべての画像をロードします。画像は.bmpまたは.jpgグラフィックスファイルです。このコマンドは、多くの画像をロードする必要があると、完了に多少の時間を要することがあります。このコマンドは、C++では使用できません。
例
autoloadimages();
現在のモデルに必要なすべての画像を再ロードします。
現在のモデルに必要なすべての画像を再ロードします。
autoloadshapes ()
説明
開発者向けです。このコマンドは、現在のビュー、ライブラリ、モデルに必要なすべての3D形状をロードします。形状は.3dsまたは.wrlファイルです。このコマンドは、多くの形状をロードする必要があると、完了に多少の時間を要することがあります。このコマンドは、C++では使用できません。
例
autoloadshapes();
現在のモデルに必要なすべての形状を再ロードします。
現在のモデルに必要なすべての形状を再ロードします。
autoloadsounds ()
説明
開発者向けです。このコマンドは、現在のビュー、ライブラリ、モデルに必要な、オブジェクトの「sound」属性で宣言されているすべてのサウンドをロードします。このコマンドは、多くのサウンドをロードする必要があると、完了に多少の時間を要することがあります。このコマンドは、C++では使用できません。
例
autoloadsounds();
現在のモデルに必要なすべてのサウンドを再ロードします。
現在のモデルに必要なすべてのサウンドを再ロードします。
flyactive ()
フライパスが存在するなら1を、存在しなければ0を返す
説明
現在実行されているフライパスが存在するなら1を、存在しなければ0を返します。
例
flyactive()
flyendnode (node x)
現在のフライパスの停止ポイントを表すノードへの参照を取得する
説明
現在のフライパスの停止ポイントを表す、ツリー内のノードへの参照を返します。
例
プレゼンテーションビルダーGUIで使用されます。
flypath (obj view, num pathno [, num singlerun])
説明
開発者向けです。このコマンドは、viewで指定されたビューの、番号がpathnoの定義済みフライパスを開始します。任意のビューウィンドウをviewとして渡すことができます。
例
flypath(ownerview(c),1);
イベントのコードを含むビューウィンドウで、番号1のフライパスを実行します。
イベントのコードを含むビューウィンドウで、番号1のフライパスを実行します。
flypathadd (obj view, num pathno)
説明
開発者向けです。このコマンドは、viewで指定されたビューの、番号がpathnoのフライパスに、フライパスを追加します。任意のビューウィンドウをviewとして渡すことができます。
例
flypathadd(ownerview(c),1);
イベントのコードを含むビューウィンドウで、フライパス番号1にフライパスを追加します。
イベントのコードを含むビューウィンドウで、フライパス番号1にフライパスを追加します。
flypathreset (obj view, num pathno)
説明
開発者向けです。このコマンドは、viewで指定されたビューの、番号がpathnoのフライパスからポイントをクリアします。ポイントがクリアされると、フライパスポイントの新しいセットを生成できます。
例
flypathreset(ownerview(c),1);
イベントのコードを含むビューで、フライパス1のフライパスポイントをクリアします。
イベントのコードを含むビューで、フライパス1のフライパスポイントをクリアします。
flystart (obj view)
説明
開発者向けです。フライモードを開始します。
例
flystart(ownerview(c))
flystop ()
説明
開発者向けです。このコマンドは、アクティブなフライパスを停止します。
例
flystop();
現在アクティブなすべてのフライパスの移動を停止します。
現在アクティブなすべてのフライパスの移動を停止します。
flyto (obj view, num endtime, num x, num y, num z, num rx, num ry, num rz)
説明
開発者向けです。指定されたビューポイントに時間をかけて移動します。
例
flyto(sv(),10000,0,0,20,-50,0,-30);
flyupdate ()
現在アクティブなフライパスを更新する
説明
現在アクティブなフライパスが存在するなら更新します。
例
getshapeindex (str name)
ロード済み3D形状のインデックスを取得する
説明
ロード済み形状のインデックスを、ファイルのパス名で取得します。このコマンドで使用するファイルパス名は、例に示すように二重のバックスラッシュを使用する必要があります。現在ロード済みの形状と、それぞれに関連付けられているファイルパス名およびインデックスの完全なリストは、[ビュー]->[メディアファイル]で表示できます。
例
getshapeindex("fs3d\\Operator\\BasicOperator\\Chest.3ds");
getsoundindex (str name)
ロード済みサウンドのインデックスを取得する
説明
project/media/soundsフォルダにあり、nameと関連付けられているロード済みサウンドのインデックスを返します。
例
getsoundindex("C:/My Sounds/APPLAUSE.WAV");
gettextureindex (str name)
ロード済み画像のインデックスを取得する
説明
ロード済み画像のインデックスを名前で取得します。FlexSimのメディアリストは、ロードされたすべてのテクスチャ(画像)のリストを保持します。それぞれのテクスチャには、対応する名前とインデックスが存在します。このコマンドは、テクスチャの名前に対応するインデックスを返します。
例
gettextureindex("myimage")
loadimage (str file, str name)
説明
開発者向けです。画像を直接ロードします。ディスク上の画像ファイルがFlexSimにロードされ、メディアリストに記録されます。FlexSimのメディアリストは、ロードされたすべての画像のリストを保持します。それぞれの画像には、対応する名前とインデックスが存在します。このコマンドは、ロードされた画像に対応するインデックスを返します。
例
loadimage("c:/myimage.bmp","myimage")
loadthreedobject (str file, str name)
説明
開発者向けです。3Dモデルを直接ロードします。ディスク上の形状ファイルがFlexSimにロードされ、メディアリストに記録されます。FlexSimのメディアリストは、ロードされたすべての形状のリストを保持します。それぞれの形状には、対応する名前とインデックスが存在します。このコマンドは、ロードされた形状に対応するインデックスを返します。
例
loadthreedobject("c:/myshape.wrl","myshape")
mediareset ()
説明
開発者向けです。すべてのメディアをアンロードします。現在ロードされているメディアすべて(画像、形状、サウンド)がFlexSimからアンロードされます。
例
mediareset()
objectsoundcode (obj object)
オブジェクトのデフォルトサウンドのインデックスを取得する
説明
オブジェクトのデフォルトサウンドのインデックスを取得します。FlexSimのメディアリストは、ロードされたすべてのサウンドのリストを保持します。それぞれのサウンドには、対応する名前とインデックスが存在します。この関数は、オブジェクトにsoundおよびsoundindex属性が存在するなら、オブジェクトのデフォルトサウンドに対応するインデックスを返します(現在のところ、デフォルトオブジェクトにはこれらの属性は存在しません)。
例
objectsoundcode(current)
shapeinfo (num info[, p1, p2, p3])
ロード済みの3D形状についての情報を取得または設定する
説明
ロード済みの3D形状についての情報を取得または設定します。
例
shapeinfo(SHAPEINFO_GET_ANIMATION_COUNT, shapeIndex);
soundchange (obj view, num sound, num volume, num tempo, num repeat, num balance)
現在再生中のサウンドを変更する
説明
現在再生中のサウンドを変更します。サウンドはオペレーティングシステムによってウィンドウに追加されるため、viewパラメータが重要になります。soundindexを取得するにはgetsoundindex()を使用します。volume、tempo、balanceは0~1の数値です。サウンドを繰り返し再生し続けるには、repeatに1を指定します。繰り返さない場合は0を指定します。オブジェクトに相対的な視点に基づいてvolumeやbalanceを変更すると、オブジェクトから音が発せられているような、おもしろい効果が得られます。
例
soundchange(sv(),1,1,1,1,.5)
soundload (str path+filename)
FlexSimにサウンドをロードする
説明
ディスク上のサウンドファイルがFlexSimにロードされ、メディアリストに記録されます。FlexSimのメディアリストは、ロードされたすべてのサウンドのリストを保持します。それぞれのサウンドには、対応する名前とインデックスが存在します。このコマンドは、ロードされたサウンドに対応するインデックスを返します。Microsoft Wave Formatファイル(.wav)をロードして再生できます。サウンドの音量、バランス、周波数は動的に調整可能です。Microsoft DirectSoundインターフェイスを使用して、複数のチャンネルを管理できます。
例
int applauseindex = soundload("c:/My Music/APPLAUSE.WAV");
soundplay (obj view, num soundindex, num volume [, num tempo, num repeat y/n, num balance])
ロード済みのサウンドを再生する
説明
ロード済みのサウンドを再生します。サウンドはオペレーティングシステムによってウィンドウに追加されるため、viewパラメータが重要になります。soundindexを取得するにはgetsoundindex()を使用します。volume、tempo、balanceは0~1の数値です。サウンドを繰り返し再生し続けるには、repeatに1を指定します。繰り返さない場合は0を指定します。
例
soundplay(sv(),3,.75,.25,1,.5)
サウンドインデックス3を選択したビューで、3/4のボリューム、1/4のテンポ、両方のスピーカーに等しいバランスで連続して再生します。
サウンドインデックス3を選択したビューで、3/4のボリューム、1/4のテンポ、両方のスピーカーに等しいバランスで連続して再生します。
soundplayfile (obj view, str path+filename, num volume [, num tempo, num repeat, num balance])
ファイルから直接サウンドを再生する
説明
ファイルから直接サウンドを再生します。サウンドはオペレーティングシステムによってウィンドウに追加されるため、viewパラメータが重要になります。volume、tempo、balanceは0~1の数値です。サウンドを繰り返し再生し続けるには、repeatに1を指定します。繰り返さない場合は0を指定します。
例
soundplayfile(sv(),"C:/My Sounds/APPLAUSE.WAV",1,1,0,.5);
soundstop (obj view, num sound)
再生中のサウンドを停止する
説明
再生中のサウンドを停止します。サウンドはオペレーティングシステムによってウィンドウに追加されるため、viewパラメータが重要になります。
例
soundstop(sv(),1)
unloadimage (int textureid)
説明
開発者向けです。インデックスを使用して画像をメディアリストからアンロードします。
例
treenode view = node("VIEW:/1>Documents/Dashboard/1+/~/GraphPanel/1/1");
repaintview(view);
viewtofile(view, modeldir() + "test.png");
unloadimage(gettextureindex(modeldir() + "test.png"));
int newindex = loadimage(modeldir() + "test.png", modeldir() + "test.png");
setobjecttextureindex(Model.find("Plane1"), newindex);
この例は、ダッシュボードチャートを画像ファイルにレンダリングし、その画像をメディアリストからアンロードして、画像をメディアリストに再ロードし、平面のテクスチャインデックスをその画像に設定します。
repaintview(view);
viewtofile(view, modeldir() + "test.png");
unloadimage(gettextureindex(modeldir() + "test.png"));
int newindex = loadimage(modeldir() + "test.png", modeldir() + "test.png");
setobjecttextureindex(Model.find("Plane1"), newindex);
この例は、ダッシュボードチャートを画像ファイルにレンダリングし、その画像をメディアリストからアンロードして、画像をメディアリストに再ロードし、平面のテクスチャインデックスをその画像に設定します。
viewtofile (obj view, str path[, num width, num height])
指定のビューをビットマップ画像として保存する
説明
指定のビューをビットマップ画像として、指定されたファイルに保存します。
例
viewtofile(node("VIEW:/active/ortho"), modeldir() + "screenshot.bmp"));
その他
カテゴリに属さないその他のコマンド。
addsystemcontrolleritem (obj systemcontroller, num productid, num linenum, num target, num starttime [, num newcolumn1, num newcolum2, num newcolum3, num newcolum4])
Dynamoで使用
説明
Dynamoで使用します。モデルの実行時に、SystemControllerのスケジュールに新しいラインアイテムを追加します。テーブルに実際に新しい行が追加されるわけではありません。パラメータは、SystemControllerのスケジュールに必要なものと同じデータです。各newcolumnパラメータは、SystemControllerのスケジュールテーブルの各行に追加されている数値です。
例
addsystemcontrolleritem(current.centerObjects[1],0,1,1,0);
commandlineparam (str param)
説明
FlexSimがコマンドラインから実行されている場合、渡された指定のコマンドラインパラメータを返します。
例
commandlineparam("nrofops");
この例は、「nrofops」コマンドラインパラメータを返します。
次の行を使用してバッチでFlexSimが開かれた場合
flexsim.exe myfile.fsm -nrofops 8
FlexSim内でcommandlineparam("nrofops")は「8」を返します。コマンドラインパラメータは、unix形式のハイフン(-)、またはWindows形式のスラッシュ(/)を使用して定義できます。
この例は、「nrofops」コマンドラインパラメータを返します。
次の行を使用してバッチでFlexSimが開かれた場合
flexsim.exe myfile.fsm -nrofops 8
FlexSim内でcommandlineparam("nrofops")は「8」を返します。コマンドラインパラメータは、unix形式のハイフン(-)、またはWindows形式のスラッシュ(/)を使用して定義できます。
contextdragconnection (obj fromobject, obj toobject, str/num characterpressed)
オブジェクト間にAまたはS接続を作成する
説明
このコマンドは、キーボードで指定の文字のキーが押されたまま、マウスでfromobjectをクリックしてtoobjectへドラッグする操作を模倣します。
このコマンドが実行されると、実際にキーボードとマウスで操作したときと同じコンテキスト依存のアクションが行われます。
このコマンドは、FlexscriptとC++のどちらでも使用できます。
このコマンドが実行されると、実際にキーボードとマウスで操作したときと同じコンテキスト依存のアクションが行われます。
このコマンドは、FlexscriptとC++のどちらでも使用できます。
例
contextdragconnection(model().subnodes[5], model().subnodes3], "A");
createcopy (node thenode, node container [, num samename, num inobject, num cached, num replace])
thenodeを指定のコンテナにコピーする
説明
containerで指定されるノードにthenodeをコピーします。このコマンドはcreateinstance()と異なり、thenodeとどのクラスとの間にもリンクの確立を試みません。インスタンスの作成が必要な場合は、この代わりにcreateinstance()を使用してください。
samenameが1なら、コピーはthenodeと同じ名前になります。
samenameが0なら、新たに作成されるノードの名前は、thenodeの名前の末尾にランダムな番号を付加したものになります。
inobjectが1なら、コンテナのオブジェクトデータ部分にコピーが作成されます。コンテナにオブジェクトデータが存在しない場合、このコマンドは何もしません。
cachedが1なら、ノードの事前キャッシュされたバージョンがコピーされます。一般に、こちらの方が高速です。
replaceが1なら、コピーはコンテナの内側に配置される代わりに、コンテナを上書きします。
これらのパラメータを指定しない場合、デフォルトは0です。
samenameが1なら、コピーはthenodeと同じ名前になります。
samenameが0なら、新たに作成されるノードの名前は、thenodeの名前の末尾にランダムな番号を付加したものになります。
inobjectが1なら、コンテナのオブジェクトデータ部分にコピーが作成されます。コンテナにオブジェクトデータが存在しない場合、このコマンドは何もしません。
cachedが1なら、ノードの事前キャッシュされたバージョンがコピーされます。一般に、こちらの方が高速です。
replaceが1なら、コピーはコンテナの内側に配置される代わりに、コンテナを上書きします。
これらのパラメータを指定しない場合、デフォルトは0です。
例
createcopy(Model.find("Tools/FlowItemBin/7/1"), current)
createinstance (obj class, obj location)
説明
開発者向けです。
このコマンドは、classで指定されたクラスのインスタンスを作成し、locationで指定されたオブジェクト内に配置します。インスタンスには、クラスの名前の後に番号が続いた名前が付けられます。インスタンスは、クラスおよびそのスーパークラスのすべての変数および属性を持ちます。動作ノード内のノードは、クラスのすべてのインスタンスに適用されるため、インスタンスにコピーされません。クラスとして渡されるオブジェクトは、ライブラリに存在する必要があります。一般に、locationはモデルです。ライブラリとモデルは、library()およびmodel()コマンドを使用して簡単に参照できます。
このコマンドは、classで指定されたクラスのインスタンスを作成し、locationで指定されたオブジェクト内に配置します。インスタンスには、クラスの名前の後に番号が続いた名前が付けられます。インスタンスは、クラスおよびそのスーパークラスのすべての変数および属性を持ちます。動作ノード内のノードは、クラスのすべてのインスタンスに適用されるため、インスタンスにコピーされません。クラスとして渡されるオブジェクトは、ライブラリに存在する必要があります。一般に、locationはモデルです。ライブラリとモデルは、library()およびmodel()コマンドを使用して簡単に参照できます。
例
createinstance(library().find("?Source"), model());
Sourceクラスのインスタンスをモデル内に作成します。
Sourceクラスのインスタンスをモデル内に作成します。
createuserlibrary ()
説明
開発者向けです。このコマンドは、新しいユーザーライブラリを作成します。
例
createuserlibrary();
deleteselected ()
説明
開発者向けです。モデル内で選択されたすべてのオブジェクトを削除します。
例
deleteselected()
dropuserlibraryobject (obj object [, obj ontoobject, num x, num y, num z, obj ontoview, num viewalreadyset])
説明
開発者向けです。指定されたオブジェクトを、ユーザーライブラリからモデルにドラッグされたのと同様にドロップします。
例
dropuserlibraryobject(node("MAIN:/project/userlibrary/1/1"));
duplicateselected ()
説明
開発者向けです。モデル内で選択されたすべてのオブジェクトを複製します。
例
duplicateselected()
executefsfile (str filename, num direct)
説明
開発者向けです。ファイルのFlexscriptコードを実行します。指定されたファイルがロードされ、コンテンツが実行されます。ファイルのコンテンツは有効なFlexscriptコードと見なされます。directが0なら、FlexSimのプログラムディレクトリがファイル名の前に連結されます。0でない場合、ファイル名がそのまま使用されます。
例
executefsfile("c:/myscript.fs",1)
filebrowse (str extension, str description, str startpath)
ファイル選択ダイアログを開く
説明
ファイル選択ダイアログを開き、ユーザーが指定のファイルタイプを選択できるようにします。複数のタイプはセミコロン(;)で区切ります。ダイアログのデフォルトディレクトリは、指定されたパスです。pdir()およびcdir()コマンドは、C++のpathパラメータとしてのみ渡すことができます。
例
string filename = filebrowse("*.fsm; *.fsp; *.fsv; *.fss","FlexSim Files",pdir());
firecreateevent (obj object, num x, num y, num z, num iscopy [, num libraryfunctiononly])
説明
開発者向けです。指定のオブジェクト作成イベントを起動します。x、y、およびzは、オブジェクトがドロップされたrzです。
例
firevalue of 0 islast(model()),0,0,0, 1);
flipselected (num firstX, num firstY, num secondX, num secondY[, node roottree])
選択されたオブジェクトを軸に対して反転する
説明
選択されたオブジェクトを、2つの渡されたxyポイントで定義される軸に対して反転します。
例
flipselected(1, 5, 2, 7)
この例は、選択されたオブジェクトをポイント(1, 5)および(2, 7)で定義される軸に対して反転します。
この例は、選択されたオブジェクトをポイント(1, 5)および(2, 7)で定義される軸に対して反転します。
geteventtime (str EventName, num mode[1/2/3])
UserEventのイベント時間を取得する
説明
UserEventのイベント時間を返します。modeは次の意味です。1 - 繰り返しの時間間隔、2 - イベントの正確な時間、3 - イベントが起動するまでの時間
例
double remainingtime = geteventtime("myevent",3);
getlastfiletype ()
説明
開発者向けです。最後に保存されたファイルのタイプを返します。1 = モデルファイル、2 = プロジェクトファイル、3 = ビューファイル、4 = セッションファイル、0 = その他のファイル
例
if (getlastfiletype()) {pt("Known file type"); pr(); }
getlinecontrollerdata (obj linecontroller, num datatype, num column)
Dynamoで使用
説明
Dynamoで使用します。LineControllerの現在のジョブに関するデータを返します。1 = ProdID、2 = LineNum、3 = Target、4 = StartTime、 5 = Extra Column
例
getlinecontrollerdata(current,1,0);
getmodelunit (num querytype)
説明
モデルの単位設定についての情報を返します。
FlexSimの標準的な単位は、時間 - 1秒、長さ - 1m、容量 - 1リットル、重量 - 1kgです。現在のモデルの単位について名前または略語を返すこともできます。
querytypeは次のいずれかの値です。
TIME_MULTIPLEは、現在のモデルの1時間単位が何秒を表すかを返します。
LENGTH_MULTIPLEは、現在のモデルの長さ単位が何メートルを表すかを返します。
FLUID_MULTIPLEは、現在のモデルの液量単位が何リットルを表すかを返します。
FLUID_TYPEは、液量単位が容積を表す場合は0、質量を表す場合は1を返します。
DATE_TIME_NODEは、モデルの単位ツリーにある日付/時刻ノードへの参照を返します。
START_TIMEは、開始時間を1601年1月1日からの秒数で返します。
START_TIME_NODEは、モデルの単位ツリーにある開始時間ノードへの参照を返します。
CURRENT_TIMEは、現在時間を1601年1月1日からの秒数で返します。
CURRENT_TIME_NODEは、モデルの単位ツリーにある現在時間ノードへの参照を返します。
STOP_TIMEは、停止時間を1601年1月1日からの秒数で返します。
STOP_TIME_NODEは、モデルの単位ツリーにある開始時間ノードへの参照を返します。
START_YEARは、開始時間に関連付けられている年を数値として返します。
START_MONTHは、開始時間に関連付けられている月を1(1月)から12(12月)までの値で返します。
START_DAYは、開始時間に関連付けられている日を返します。1が月の最初の日を示します。
START_DAYOFWEEKは、開始時間に関連付けられている曜日を数値で返します。0が日曜日です。
START_HOURは、開始時間に関連付けられている時間を0~23の数値で返します。
START_MINUTEは、開始時間に関連付けられている分を0~59の数値で返します。
START_SECONDは、開始時間に関連付けられている秒を0~59の数値で返します。
START_MILLISECONDは、開始時間に関連付けられているミリ秒を0~999の数値で返します。
CURRENT_YEARは、モデルの開始時間からの年数を返します。
CURRENT_DAYは、モデルの開始時間からの日数を返します。
CURRENT_HOURは、モデルの開始時間からの時間数を返します。
CURRENT_MINUTEは、モデルの開始時間からの分数を返します。
CURRENT_SECONDは、モデルの開始時間からの秒数を返します。
CURRENT_MILLISECONDは、モデルの開始時間からのミリ秒数を返します。
CURRENT_YEAR_OF_TIMEは、現在の時刻に関連付けられている年を数値として返します。
CURRENT_MONTH_OF_YEARは、現在の時刻に関連付けられている月を1(1月)から12(12月)までの値で返します。
CURRENT_DAY_OF_MONTHは、現在の時刻に関連付けられている日を数値で返します。1が月の最初の日を示します。
CURRENT_DAY_OF_WEEKは、現在の時刻に関連付けられている曜日を数値で返します。0が日曜日です。
CURRENT_HOUR_OF_DAYは、現在の時刻に関連付けられている時間を0~23の数値で返します。
CURRENT_MINUTE_OF_HOURは、現在の時刻に関連付けられている分を0~59の数値で返します。
CURRENT_SECOND_OF_MINUTEは、現在の時刻に関連付けられている秒を0~59の数値で返します。
CURRENT_MILLISECOND_OF_SECONDは、現在の時刻に関連付けられているミリ秒を0~999の数値で返します。
TIME_NAMEは、モデルの時間単位の名前を返します。
TIME_PLURAL_NAMEは、モデルの時間単位の複数名を返します。
TIME_ABBREVIATIONは、モデルの時間単位の略語を返します。
LENGTH_NAMEは、モデルの長さ単位の名前を返します。
LENGTH_PLURAL_NAMEは、モデルの長さ単位の複数名を返します。
LENGTH_ABBREVIATIONは、モデルの長さ単位名の略語を返します。
FLUID_NAMEは、モデルの液量単位の名前を返します。
FLUID_PLURAL_NAMEは、モデルの液量単位の複数名を返します。
FLUID_ABBREVIATIONは、モデルの液量単位名の略語を返します。
START_TIME_STRは、開始時間を日付と時刻の形式で文字列として返します。
CURRENT_TIME_STRは、現在の時刻を日付と時刻の形式で文字列として返します。
STOP_TIME_STRは、停止時間を日付と時刻の形式で文字列として返します。
TIME_FORMATは、日付と時刻の文字列のフォーマットに使用される時間形式を返します。
DATE_FORMATは、日付と時刻の文字列のフォーマットに使用される日付形式を返します。
FlexSimの標準的な単位は、時間 - 1秒、長さ - 1m、容量 - 1リットル、重量 - 1kgです。現在のモデルの単位について名前または略語を返すこともできます。
querytypeは次のいずれかの値です。
TIME_MULTIPLEは、現在のモデルの1時間単位が何秒を表すかを返します。
LENGTH_MULTIPLEは、現在のモデルの長さ単位が何メートルを表すかを返します。
FLUID_MULTIPLEは、現在のモデルの液量単位が何リットルを表すかを返します。
FLUID_TYPEは、液量単位が容積を表す場合は0、質量を表す場合は1を返します。
DATE_TIME_NODEは、モデルの単位ツリーにある日付/時刻ノードへの参照を返します。
START_TIMEは、開始時間を1601年1月1日からの秒数で返します。
START_TIME_NODEは、モデルの単位ツリーにある開始時間ノードへの参照を返します。
CURRENT_TIMEは、現在時間を1601年1月1日からの秒数で返します。
CURRENT_TIME_NODEは、モデルの単位ツリーにある現在時間ノードへの参照を返します。
STOP_TIMEは、停止時間を1601年1月1日からの秒数で返します。
STOP_TIME_NODEは、モデルの単位ツリーにある開始時間ノードへの参照を返します。
START_YEARは、開始時間に関連付けられている年を数値として返します。
START_MONTHは、開始時間に関連付けられている月を1(1月)から12(12月)までの値で返します。
START_DAYは、開始時間に関連付けられている日を返します。1が月の最初の日を示します。
START_DAYOFWEEKは、開始時間に関連付けられている曜日を数値で返します。0が日曜日です。
START_HOURは、開始時間に関連付けられている時間を0~23の数値で返します。
START_MINUTEは、開始時間に関連付けられている分を0~59の数値で返します。
START_SECONDは、開始時間に関連付けられている秒を0~59の数値で返します。
START_MILLISECONDは、開始時間に関連付けられているミリ秒を0~999の数値で返します。
CURRENT_YEARは、モデルの開始時間からの年数を返します。
CURRENT_DAYは、モデルの開始時間からの日数を返します。
CURRENT_HOURは、モデルの開始時間からの時間数を返します。
CURRENT_MINUTEは、モデルの開始時間からの分数を返します。
CURRENT_SECONDは、モデルの開始時間からの秒数を返します。
CURRENT_MILLISECONDは、モデルの開始時間からのミリ秒数を返します。
CURRENT_YEAR_OF_TIMEは、現在の時刻に関連付けられている年を数値として返します。
CURRENT_MONTH_OF_YEARは、現在の時刻に関連付けられている月を1(1月)から12(12月)までの値で返します。
CURRENT_DAY_OF_MONTHは、現在の時刻に関連付けられている日を数値で返します。1が月の最初の日を示します。
CURRENT_DAY_OF_WEEKは、現在の時刻に関連付けられている曜日を数値で返します。0が日曜日です。
CURRENT_HOUR_OF_DAYは、現在の時刻に関連付けられている時間を0~23の数値で返します。
CURRENT_MINUTE_OF_HOURは、現在の時刻に関連付けられている分を0~59の数値で返します。
CURRENT_SECOND_OF_MINUTEは、現在の時刻に関連付けられている秒を0~59の数値で返します。
CURRENT_MILLISECOND_OF_SECONDは、現在の時刻に関連付けられているミリ秒を0~999の数値で返します。
TIME_NAMEは、モデルの時間単位の名前を返します。
TIME_PLURAL_NAMEは、モデルの時間単位の複数名を返します。
TIME_ABBREVIATIONは、モデルの時間単位の略語を返します。
LENGTH_NAMEは、モデルの長さ単位の名前を返します。
LENGTH_PLURAL_NAMEは、モデルの長さ単位の複数名を返します。
LENGTH_ABBREVIATIONは、モデルの長さ単位名の略語を返します。
FLUID_NAMEは、モデルの液量単位の名前を返します。
FLUID_PLURAL_NAMEは、モデルの液量単位の複数名を返します。
FLUID_ABBREVIATIONは、モデルの液量単位名の略語を返します。
START_TIME_STRは、開始時間を日付と時刻の形式で文字列として返します。
CURRENT_TIME_STRは、現在の時刻を日付と時刻の形式で文字列として返します。
STOP_TIME_STRは、停止時間を日付と時刻の形式で文字列として返します。
TIME_FORMATは、日付と時刻の文字列のフォーマットに使用される時間形式を返します。
DATE_FORMATは、日付と時刻の文字列のフォーマットに使用される日付形式を返します。
例
getmodelunit(LENGTH_MULTIPLE)
getreportnum (node report, int column, int rowsback)
Dynamoで使用
説明
Dynamoで使用します。Reportオブジェクトの指定された列にある値を返します。行は、テーブル内の行数からrowsbackパラメータを減算して求められます。
例
double myval = getreportnum(current,3,0);
groupsetnames (node namenode, num startnum, num append)
説明
開発者向けです。モデル内で選択されたすべてのオブジェクトの名前を、namenodeの文字列データに設定します。appendが1なら、それぞれの名前の末尾に数値が付加されます。この数値はstartnumから始まり、オブジェクトごとに1ずつ増やされます。
例
groupsetnames("WeldStation",1,1);
hideprogressbar ()
説明
開発者向けです。進行状況バーを非表示にします。
例
hideprogressbar();
highestconnection ()
番号が最も大きいサーバー接続インデックスを取得する
説明
番号が最も大きいサーバー接続インデックスを返します。
例
int highconn = highestconnection();
insertcopy (obj originalobject, obj containerobject)
フローアイテムのコピーを作成し、コンテナオブジェクトに移動する
説明
フローアイテムのコピーを作成し、コンテナオブジェクトに移動します。これにより、コンテナのOnReceiveイベントが実行されます。
例
insertcopy(item, current);
フローアイテムの複製を作成し、currentオブジェクトに移動します。
フローアイテムの複製を作成し、currentオブジェクトに移動します。
integrityscan (obj class, obj start)
説明
開発者向けです。モデルのオブジェクトから属性が削除されていないかを、クラスオブジェクトに基づいてチェックします。与えられた開始ノードから検索が実行されます。
例
integrityscan(rank(library(1)),model())
isprojectcompiled ()
説明
開発者向けです。プロジェクトがコンパイル済みなら1を返します。
例
isprojectcompiled()
loadselectedfromfile (obj highlightedobj)
説明
開発者向けです。以前に保存されたツリーファイルを、強調表示されているオブジェクトにロードします。
例
loadselectedfromfile(selectedobject(ownerview(c)))
loadstate ()
説明
開発者向けです。プロジェクトの状態をロードします。savestate()がすでに実行されている場合、モデルを再度実行する前にこのコマンドを実行する必要があります。
例
loadstate();
loaduserlibrary (str libfile [, obj libraryview, num reloadmedia, num changeitemcurrent, num autoinstall])
説明
開発者向けです。libfileで指定されたパスからライブラリをロードします。reloadmediaが真のとき、ライブラリのロード後にautoloadallmedia()が呼び出されます。autoinstallが真のとき、ライブラリのロードと新規モデルのautoinstallオブジェクトがモデルに追加されます。libraryviewおよびchangeitemcurrentパラメータは、現在は使用されません。
例
loaduserlibrary(cdir() + "libraries/mylib.fsl");
memberadd (obj childobject, str parentname, num type)
説明
type = 1なら、「parentname」という名前のタイムテーブルにメンバーとしてchildobjectを追加します。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトにメンバーとしてchildobjectを追加します。
このコマンドは、各種のシフトにオペレーターを動的に割り当てるためなどに便利です。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトにメンバーとしてchildobjectを追加します。
このコマンドは、各種のシフトにオペレーターを動的に割り当てるためなどに便利です。
例
memberadd(model().subnodes[2],"TimeTable1",1)
memberremove (obj childobject, str parentname, num type)
説明
type = 1なら、「parentname」という名前のタイムテーブルのメンバーからchildobjectを削除します。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトのメンバーからchildobjectを削除します。
memberadd()を参照してください。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトのメンバーからchildobjectを削除します。
memberadd()を参照してください。
例
memberremove(model().subnodes[2],"TimeTable1",1)
memberremoveall (str parentname, num type)
説明
type = 1なら、「parentname」という名前のタイムテーブルからすべてのメンバーを削除します。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトからすべてのメンバーを削除します。
memberremove()を参照してください。
type = 2なら、「parentname」という名前のMTBFMTTRオブジェクトからすべてのメンバーを削除します。
memberremove()を参照してください。
例
memberremoveall("TimeTable1",1)
moveobject (obj object, obj location[, num outport])
オブジェクトを指定の場所に移動する
説明
このコマンドは、オブジェクトを指定のポート経由で、指定の場所へ移動します。指定されたポートが実際に存在する必要はありません。この値は受信側の場所が、オブジェクトがどのポートから来たのかを参照可能にするためのものです。オブジェクトが場所に移動するとき、その場所のOnReceiveイベント関数が実行されます。これには、OnEntryトリガー関数も含まれます。イベントがキューに置かれた状態で、フローアイテムに対して明示的にこのコマンドを呼び出すと、問題が発生することがあります。移動対象のオブジェクトについて保留中のイベントが存在しないのが明らかな場合のみ使用してください。
例
moveobject(current.first,current.centerObjects[1]);
currentにより参照されるオブジェクト内に存在する最初のオブジェクトを、currentの最初のセンターポートに接続されているオブジェクトに移動します。
currentにより参照されるオブジェクト内に存在する最初のオブジェクトを、currentの最初のセンターポートに接続されているオブジェクトに移動します。
moveselectedintohighlighted (obj highlightedobj [, node selectedcontainer])
説明
開発者向けです。モデル内で選択されたすべてのオブジェクトを、強調表示されているオブジェクトに移動します。
例
moveselectedintohighlighted(selectedobject(ownerview(c)))
nametomodelpath (obj node, obj object)
notifylinecontroller (node object, int controllernum, num output, num sendinglast [0/1])
Dynamoで使用
説明
Dynamoで使用します。オブジェクトに接続されているLineControllerに対して、材料がラインを離れたため、実行が完了したかどうかをControllerが決定できることを通知します。通知を受けるLineControllerの番号は、contollernumパラメータで指定されます。オブジェクトは、モデルが実行を開始した後でどれだけの量の材料(種類を問わず)が退出したのか、および退出した材料がオブジェクトの最後の材料かどうかを報告します。
例
notifylinecontroller(current,1,current.stats.output + 1,(current.subnodes.length == 1));
pickoptiononselect (obj view)
説明
開発者向けです。このコマンドは、ピックリストのguiコントロールで、オプションが選択されたときのコンボボックスのテキストを変更するため使用されます。
例
pickoptiononselect(c);
rotateselected (double angle, double x, double y[, obj roottree])
説明
モデル内の選択されたすべてのオブジェクトを、割り当てられた原点のx/y位置の周囲で回転します。
例
rotateselected(90, 5, 0)
この例は、選択されたオブジェクトを場所(5,0)の周囲で90度回転します。
この例は、選択されたオブジェクトを場所(5,0)の周囲で90度回転します。
savebyname (obj tree, str filename)
説明
開発者向けです。指定されたツリーノードを、与えられた名前のファイルに保存します。
例
savebyname(Model.find("MyProcessor"), "C:\\MyProcessor.t");
savemodelprepare ()
説明
開発者向けです。モデルを保存する準備としてリセットなどの処理を行います。
例
savemodelprepare();
saveselectedtofile ()
説明
開発者向けです。モデル内で選択されたすべてのオブジェクトを、ツリーファイルに保存します。
例
saveselectedtofile()
savestate ()
説明
開発者向けです。プロジェクトの状態を保存します。このコマンドが実行されると、プロジェクト(.fsp)を保存して、後で開いてコンパイル、loadstate()の実行、および以前に開始したスポットからの実行を行えます。
例
savestate();
savetree (node tree, str extension, str description, str startingpath)
説明
開発者向けです。ファイルの保存ダイアログを開き、保存するファイル名の入力をユーザーに求めます。渡されるツリーは、セッションが選択されていない限り、指定の名前で保存されます。その場合、最初のパラメータは無視されます。FlexScriptでは、cdir()およびpdir()をパスとして直接使用できません。
例
savetree(model(),"fsm","FlexSim Model",documentsdir());
searchfornode (str/node searchstr, node startnode, num findnr[, num searchobjects])
説明
開発者向けです。startnodeから、searchstrを含む名前を持つノードを再帰的に検索します。findnrパラメータは、与えられた名前を含むノードが検索により複数見つかった場合に有用です。このパラメータに数値iを指定すると、i番目に見つかったノードが返されます。searchobjectsに1を設定すると、オブジェクトのデータノードが検索されます。
例
seteventtime (str EventName, num time, num timemode[1/2], num createevent[1/0])
グローバルUserEventの「繰り返しのイベント時間」を設定する
説明
指定されたグローバルUserEventの「繰り返しのイベント時間」を設定します。timemode = 1なら、timevalが直接使用されます。それ以外の場合、timeval - time()が使用されます。createevent = 1なら、「繰り返しのイベント時間」の更新に加えて、以前に指定された時間に単一のイベントが作成されます。
例
seteventtime("UserEvent1",20,1,0);
「UserEvent1」という名前のグローバルusereventの「繰り返しのイベント時間」を20に設定します。
「UserEvent1」という名前のグローバルusereventの「繰り返しのイベント時間」を20に設定します。
setprogressbar (num progress)
説明
開発者向けです。進行状況バーを指定された値に設定します。値は0~100の範囲です。
例
setprogressbar((numread / numtotal) * 100);
showprogressbar (str caption)
説明
開発者向けです。指定されたキャプション付きで進行状況バーを開きます。バーの進行状況は0に初期化されます。進行状況の値を更新するにはsetprogressbarを使用します。
例
showprogressbar("Loading data, please wait");
so ()
so()として割り当てられた最後のノードへの参照を取得する
説明
このコマンドは、選択されたオブジェクトを割り当てられた最後のノードへの参照を返します。このコマンドは、スクリプトウィンドウでのみ使用されます。ノードをsoとして割り当てるには、ツリー内のノードを右クリックし、[編集]|[このノードを指定(so)]を選択します。ツリー内のどのノードにも、選択されたオブジェクトを割り当てできます。
例
getnodename(so())
選択されたオブジェクトを現在割り当てられているオブジェクトの名前を返します。このコマンドは一般に、スクリプトウィンドウでのみ使用されます。スクリプトウィンドウでは、最後のセミコロン(;)は必要ありません。
選択されたオブジェクトを現在割り当てられているオブジェクトの名前を返します。このコマンドは一般に、スクリプトウィンドウでのみ使用されます。スクリプトウィンドウでは、最後のセミコロン(;)は必要ありません。
startuploadlibraries ([num viewalreadyset])
説明
開発者向けです。スタートアップ時にライブラリをロードします。
例
startuploadlibraries()
transfernodeobj (node movenode, node container)
movenodeをcontainerノードのオブジェクトデータに移動する
説明
このコマンドはmovenodeを、containerノードのオブジェクトデータに移動します。これはmoveobjectコマンドとほぼ同じですが、イベント(OnSend、OnReceive)が実行されない点が異なります。
例
transfernodeobj(current.attrs.find("body"), current.next);
updatereport (num/str/node report)
Dynamoで使用
説明
Dynamoで使用します。指定されたReportをテーブルの新しい行に追加し、正しく入力します。時間ベースでないエントリを追加するために使用されます。
例
updatereport("ResultsReport");
userinput (obj targetnode, str text)
ダイアログボックスで値の入力をユーザーに求める
説明
ダイアログボックスで値の入力をユーザーに求めます。この値は指定されたノードに置かれます。ダイアログが開いている間、モデルの実行は停止しません。
例
userinput(model().subnodes[3].labels["myLabel"],"Please enter a value");
validatename (obj node, num isviewtext [, obj object])
説明
開発者向けです。ノードの名前をFlexSimの有効な名前にするため、無効な文字をアンダースコアに置き換え、変更が行われ場合はメッセージを表示します。isviewtextが1なら、渡されたノードは編集フィールドと見なされ、ノードの名前の代わりにフィールドのviewtextが変更されます。objectパラメータが指定された場合、コンテナに存在する他のすべてのオブジェクト名に対して、オブジェクト名がチェックされます。同じ名前が存在する場合、エラーメッセージが表示されます。このコマンドは、オブジェクトの[プロパティ]ウィンドウで[適用]または[OK]ボタンが押されたとき呼び出されます。
例
validatename(current, 0);
モデル実行
シミュレーションの実行を停止、開始、管理するためのコマンド。
endreplication (num onlyifexperimenting)
現在の実験ツールの複製を終了する
説明
現在の実験ツールの複製を終了します。実験ツールの終了時間が設定されておらず、特定の条件が真になることで終了する場合に使用します。onlyifexperimentingに1を指定すると、実験の実行中のみ停止が行われます。
例
if(current.stats.output >= 5000) endreplication(1);
getrunstate ()
モデルが現在実行中なら1を、そうでなければ0を返す
説明
モデルが現在実行中なら1を、そうでなければ0を返します。
例
if(!getrunstate()){msg("Model Stopped", "The model is not running right now.",1);}
スクリプトウィンドウから実行すると、モデルが停止している場合のみメッセージが表示されます。
スクリプトウィンドウから実行すると、モデルが停止している場合のみメッセージが表示されます。
go ([num fast])
シミュレーションの実行を開始する
説明
このコマンドは、シミュレーションの実行を開始します。イベントキューにイベントが存在する場合、クロックがそのイベントに到達したときに発生します。キューにイベントがなければ、クロックは停止します。このコマンドはシミュレーションをリセットしません。fastが1なら、開始前にオブジェクトをバインドしません。これにより、シミュレーションの停止と開始を頻繁に行うときに速度が向上します。runfunction()も参照してください。
例
stop();
if (msg("Model Stopped","Continue?")==1)
{
go();
}
モデルを停止してから、再開するかどうかの入力をユーザーに求めます。ユーザーが[OK]を押すと、モデルは停止した場所から続行されます。
if (msg("Model Stopped","Continue?")==1)
{
go();
}
モデルを停止してから、再開するかどうかの入力をユーザーに求めます。ユーザーが[OK]を押すと、モデルは停止した場所から続行されます。
realtime (num timecode)
リアルクロック時間を取得する
説明
timecodeに基づいて、さまざまな形式でリアルクロック時間を返します。
1 = 1970年1月1日の真夜中からの秒数
2 = 最後に秒が変化してからのミリ秒の数
10 = hh:mm:ss形式の時間文字列
11 = mm/dd/yy形式の日付文字列
12 = Mon Nov 15 15:49:12 2004の形式の日付と時間の文字列
1 = 1970年1月1日の真夜中からの秒数
2 = 最後に秒が変化してからのミリ秒の数
10 = hh:mm:ss形式の時間文字列
11 = mm/dd/yy形式の日付文字列
12 = Mon Nov 15 15:49:12 2004の形式の日付と時間の文字列
例
string curdatetime = realtime(12);
resetexperiment ()
説明
開発者向けです。完全なモデルのリセットを行わず、実験をリセットします。通常は、実験マネージャーにより内部的に使用されます。
例
resetexperiment()
resetlayer (obj layer)
説明
開発者向けです。渡されたレイヤーをリセットします。代わりにresetmodelを使用してください。
例
resetmodel ([num buildflexscript])
モデルをリセットする
説明
モデルをリセットします。reset()の代わりにこのコマンドを使用してください。パラメータは、エンジンがすべてのflexscript関数も構築するかどうかを指定します。
例
resetmodel()
resetstats ()
説明
開発者向けです。完全なモデルのリセットを行わず、すべてのオブジェクト統計をリセットします。通常は、実験マネージャーにより内部的に使用されます。
例
resetstats()
runfunction ()
説明
開発者向けです。ユーザーの入出力をブロックし、cpuで可能な最高速でモデルを実行して、stoptimeが満たされたときに制御を返します。stoptime = 0なら、stoptimeは1000と見なされます。go()を参照してください。
例
runfunction()
runspeed (num speed[, num precisionMode])
シミュレーションの速度を設定する
説明
このコマンドは、シミュレーションの実行速度を設定します。[実行コントロール]ウィンドウのスライバーバーをクリックしてドラッグするのと同じですが、より正確です。モデルが実行を試みる速度は、実際の秒あたりのシミュレーション時間単位の数で定義されます。コンピュータのcpuがその速度に追い付けない場合、モデルが実際にその速度で実行されるとは限りません。precisionModeは、使用する精度を定義します。0なら、精度モードは呼び出し前と同じに維持されます。RUN_SPEED_LOW_PRECISIONを渡すと、低精度の実行速度に設定されます。RUN_SPEED_HIGH_PRECISIONを渡すと、高精度モードで実行されます。これは、エミュレーションの目的で使用されます。精度モードはリセットごとに低精度にリセットされるため、高精度モードを有効にするには、リセット時またはモデルの開始時に設定を高精度に戻すメカニズムが必要です。
例
runspeed(10);
go();
シミュレーションの速度を、実際の1秒ごとにシミュレーションの10秒に設定してから、モデルを実行します。
go();
シミュレーションの速度を、実際の1秒ごとにシミュレーションの10秒に設定してから、モデルを実行します。
step ()
説明
開発者向けです。モデルの実行を1ステップだけ進めます。1ステップは、正確に1イベントの処理を意味します。
例
step()
stop ([num fast])
シミュレーションの実行を停止する
説明
このコマンドは、シミュレーションクロックの実行を停止します。モデルは停止し、保留中のイベントはすべてキューに維持されます。ユーザーがリセット前にモデルを再開した場合、モデルは正確に停止した時点から続行します。fastが1なら、FlexSimはオブジェクトを再バインドしません。これにより、停止と開始を頻繁に行うときに速度が向上します。
例
stop()
stoptime (num time)
シミュレーションが停止する時間を設定する
説明
このコマンドは、シミュレーションが実行を停止する時間を設定します。モデルは正確に指定された時間で停止するとは限りませんが、指定された停止時間、またはそれ以後で最初のシステムチェック時に停止します。実行するイベントが残っていなければ、モデルはそれより早く停止することもあります。timeが-1なら、このコマンドは現在の停止時間を返します。
例
if (stoptime(-1) < 500)
stoptime(500);
stoptimeが500より小さければ、500に設定します。
stoptime(500);
stoptimeが500より小さければ、500に設定します。
updatestates ()
モデル内のすべてのオブジェクトの状態を更新する
説明
モデル内のすべてのオブジェクトの状態を更新します。また、このコマンドはすべてのオブジェクトのコンテンツ統計も更新します。[停止]ボタンとメニューオプションはどちらも、オブジェクトの統計を更新するため、stop()を実行する前にこの関数を呼び出します。これを行わないと、レポートはオブジェクトが最後の状態であった時間を反映しません。
例
updatestates();
ネットワークノード
ネットワークノードオブジェクトとネットワークパスに関連するコマンド。
closenodeedge (obj object, num edgenum)
ネットワークノードのエッジへのエントリを閉じる
説明
ネットワークノードの指定されたエッジ番号へのエントリを閉じます。
エッジの色がオレンジに変わり、閉じたことを示します。
エッジが開いている/閉じているのステータスは、移動者が
ノードから次のノードへ移動するときのみチェックされます(オフセットからノードに進入するときではなく)。
エッジの色がオレンジに変わり、閉じたことを示します。
エッジが開いている/閉じているのステータスは、移動者が
ノードから次のノードへ移動するときのみチェックされます(オフセットからノードに進入するときではなく)。
例
closenodeedge(current.centerObjects[1], 3);
getedgedist (obj netnode, num edgenum)
ネットワークノードのエッジの距離を取得する
説明
ネットワークノードの指定されたエッジの距離を返します。
例
getedgedist(current, 1)
getedgespeedlimit (obj netnode, num edgenum)
ネットワークノードのエッジの制限速度を取得する
説明
ネットワークノードの指定されたエッジの制限速度を返します。
例
getedgespeedlimit(current, 1)
getnetnode (obj object, num nodenr)
A接続ラインを持つオブジェクトに接続されている、n番目のネットワークノードを取得する
説明
「青」または「ステーション」接続ラインを持つオブジェクトに接続されている、n番目のネットワークノードを返します。
例
getnetnode(current, 1)
getnetnodespline (obj netnode, num edgenr)
netnodeのエッジedgenrのスプラインヘッドへの参照を取得する
説明
ネットワークノードの指定されたエッジのスプラインヘッドへの参照を返します。その後でspline()コマンドを使用し、そのスプラインの場所データにアクセスできます。スプラインヘッドは、渡されるネットワークノードの中にある必要はなく、エッジの反対側のネットワークノードに存在していてもかまわないことに注意してください。isedgeforward()コマンドを使用して、スプラインがネットワークノード内に存在するかどうかを照会できます。存在しない場合、spline()コマンドに渡されるスプラインのパーセンテージ距離は逆方向になります。
例
treenode splinehead = getnetnodespline(netnode, 2);
getnetworkdistance (num fromnetnoderank, num tonetnoderank)
2つのネットワークノード間のネットワーク距離を取得する
説明
ネットワークノード間のネットワーク距離を返します。ネットワークノードは、ネットワークノードへのポインターではなくメンバーランクで参照されることに注意してください。ネットワークノードのメンバーランクを取得するには、rankfromnetnode()を使用してください。
例
getnetworkdistance(rankfromnetnode(current), rankfromnetnode(current.outObjects[1]));
getnextnetnode (num fromnn, num tonn)
fromnnからtonnに到達するための、次のネットワークノードのランクを取得する
説明
あるネットワークノードから目的地のネットワークノードへ移動するための、次のネットワークノードのランクを返します。戻り値とパラメータはすべて、ネットワークノードのメンバーランクです。ネットワークノードのメンバーランクを取得するにはrankfromnetnode()を、メンバーランクからネットワークノードを取得するにはnetnodefromrank()を使用してください。
例
treenode nextnode = netnodefromrank(getnextnetnode(rankfromnetnode(current), rankfromnetnode(Model.find("NN5"))));
getnextnetnodeoutport (num fromnn, num tonn)
ネットワークノードfromnnからtonnに到達するための出力ポートを取得する
説明
ソースネットワークノードから目的地ネットワークノードに到達するため使用される出力ポート、またはエッジ番号を返します。
例
int outport = getnextnetnodeoutport(rankfromnetnode(current), rankfromnetnode(Model.find("NN5")));
gettenetnode (obj taskexecuter)
taskexecuterがA接続によってアタッチされている現在のネットワークノードを取得する
説明
taskexecuter(TE)が赤い線によってアタッチされている現在のネットワークノードを返します。
例
treenode netnode = gettenetnode(current);
gettenetworkinfo (obj taskexecuter, obj destobj, num info)
ノードネットワークのtaskexecuterの現在の状態に関する情報を取得する
説明
ノードネットワークのtaskexecuterの現在の状態に関する情報を返します。有効なクエリは次のとおりです。
NETWORK_INFO_DEST_NET_NODE_RANK - TEがdestobjへの移動タスクを与えられたとき、移動する目的地のネットワークノードの列/ランクを返します。これは通常はdestobjにアタッチされているネットワークノードですが、複数のネットワークノードがdestobjにアタッチされている場合、このコマンドは最も近いものを返します。
NETWORK_INFO_ORIGIN_NET_NODE_RANK - TEがdestobjへの移動タスクを与えられたとき、開始点となるネットワークノードの列/ランクを返します。これは通常はTEが置かれている現在のネットワークノードですが、そのネットワークに仮想出口が存在する場合、このコマンドは移動距離が最も短くなる仮想出口を返します。
NETWORK_INFO_DISTANCE - ネットワーク経由で目的地オブジェクトへの最も短い移動距離を返します。
NETWORK_INFO_CUR_DIST_ALONG_EDGE - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在のネットワークエッジに沿って移動した現在の距離を返します。このクエリでは、destobjにNULLを指定します。
NETWORK_INFO_CUR_TRAVEL_ORIGIN_RANK - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在の移動オペレーションを開始した元のノードのランクを返します。このクエリでは、destobjにNULLを指定します。
NETWORK_INFO_CUR_TRAVEL_DEST_RANK - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在の移動オペレーションにより移動する目的地のノードのランクを返します。このクエリでは、destobjにNULLを指定します。
NETWORK_INFO_DEST_NET_NODE_RANK - TEがdestobjへの移動タスクを与えられたとき、移動する目的地のネットワークノードの列/ランクを返します。これは通常はdestobjにアタッチされているネットワークノードですが、複数のネットワークノードがdestobjにアタッチされている場合、このコマンドは最も近いものを返します。
NETWORK_INFO_ORIGIN_NET_NODE_RANK - TEがdestobjへの移動タスクを与えられたとき、開始点となるネットワークノードの列/ランクを返します。これは通常はTEが置かれている現在のネットワークノードですが、そのネットワークに仮想出口が存在する場合、このコマンドは移動距離が最も短くなる仮想出口を返します。
NETWORK_INFO_DISTANCE - ネットワーク経由で目的地オブジェクトへの最も短い移動距離を返します。
NETWORK_INFO_CUR_DIST_ALONG_EDGE - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在のネットワークエッジに沿って移動した現在の距離を返します。このクエリでは、destobjにNULLを指定します。
NETWORK_INFO_CUR_TRAVEL_ORIGIN_RANK - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在の移動オペレーションを開始した元のノードのランクを返します。このクエリでは、destobjにNULLを指定します。
NETWORK_INFO_CUR_TRAVEL_DEST_RANK - TEが移動タスクをアクティブに実行中のときのみ有効です。TEが現在の移動オペレーションにより移動する目的地のノードのランクを返します。このクエリでは、destobjにNULLを指定します。
例
int destrank = gettenetworkinfo(current, NULL, NETWORK_INFO_CUR_TRAVEL_DEST_RANK);
isedgeforward (obj netnode, num edgenr)
ネットワークノードのエッジが順方向なら1を、そうでなければ0を返す
説明
ネットワークノードのエッジが「順方向」、すなわち作成時に接続がこのネットワークノードから他のネットワークノードに向けてドラッグされた場合、1を返します。エッジが順方向の場合、スプラインヘッドはこのネットワークノードに含まれ、スプライン距離の値はこのネットワークから順方向に計算されます。
例
isedgeforward(current, 2)
netnodefromrank (num rank)
ネットワークノードのランクrankにあるメンバーを返す
説明
ネットワークノードのメンバーランクを取得し、ネットワークノードへの実際の参照を返します。
例
treenode netnode = netnodefromrank(5);
opennodeedge (obj networknode, num edgenum)
ネットワークノードのエッジへのエントリを開く
説明
ネットワークノードの指定されたエッジ番号へのエントリを開きます。ノードのエッジをclosenodeedge()で閉じると、移動者はエッジに進入できなくなります。このコマンドはエッジを再度開きます。
例
opennodeedge(current.centerObjects[1], 3);
currentオブジェクトのセンターポート1に接続されているネットワークノードの、ノードエッジ3を開きます。
currentオブジェクトのセンターポート1に接続されているネットワークノードの、ノードエッジ3を開きます。
optimizenetwork ()
モデルのネットワークナビゲータで、距離テーブルを再生成する
説明
モデルのネットワークナビゲータで、距離テーブルを再生成します。
このコマンドは、シミュレーション実行時にネットワーク内のエッジを動的に接続するとき使用します。
大きなネットワークでは、この動作に数秒を要することがあります。
このコマンドは、シミュレーション実行時にネットワーク内のエッジを動的に接続するとき使用します。
大きなネットワークでは、この動作に数秒を要することがあります。
例
optimizenetwork()
rankfromnetnode (obj netnode)
ネットワークノードnetnodeのメンバーランクを返す
説明
ネットワークノードの参照を取得し、そのネットワークノードのメンバーランクを返します。各ネットワークノードには固有の「メンバーランク」が存在し、ネットワークの距離および次のノードのテーブルで、行/列の参照として使用されます。モデルに最初に追加されたネットワークノードがメンバーランク1、2番目がメンバーランク2の順に番号が付けられます。
例
int memberrank = rankfromnetnode(current);
reassignnetnode (obj taskexecuter, obj networknode)
説明
ネットワークノードシステムを使用するTaskExecuterは、システム内の特定のネットワークノード(赤い線のグラフィックス)と常に関連付けられていますが、これは移動に伴って変化し続けます。このコマンドは、指定されたtaskexecuterをネットワークノードに再割り当てします。
警告:このコマンドは、TaskExecuterがネットワーク上に存在し、現在移動タスクを実行中でないことが明らかな場合のみ実行してください。
警告:このコマンドは、TaskExecuterがネットワーク上に存在し、現在移動タスクを実行中でないことが明らかな場合のみ実行してください。
例
reassignnetnode(current, current.centrObjects[5]);
現在のTaskExecuterを、5番目のセンターポートに接続されているネットワークノードに再割り当てします。
現在のTaskExecuterを、5番目のセンターポートに接続されているネットワークノードに再割り当てします。
redirectnetworktraveler (obj traveler, obj newdest)
説明
travelerの最終目的地を、newdestオブジェクトのものに変更する操作を試みます。travelerが現在TASKTYPE_TRAVELタスクを実行中で、移動ネットワークに存在する場合のみ動作します。成功した場合は1を返します。
例
redirectnetworktraveler(traveler, Model.find("Processor5"));
travelerが、現在ネットワークノードシステム上を移動中のtaskexecuterへのポインターで、Processor5がネットワークに接続されていると想定し、モデル内でProcessor5という名前のオブジェクトにtravelerをリダイレクトします。
travelerが、現在ネットワークノードシステム上を移動中のtaskexecuterへのポインターで、Processor5がネットワークに接続されていると想定し、モデル内でProcessor5という名前のオブジェクトにtravelerをリダイレクトします。
trafficcontrolinfo (obj trafficcontrol, num info [, num a, num b])
トラフィックコントローラーについての情報を取得する
説明
このコマンドを使用して、トラフィック制御についての各種の情報にアクセスし、トラフィック制御でロジックを実行するよう指示できます。実行されるロジックや返されるデータは、infoパラメータによって次のように指定されます。
trafficcontrolinfo(tc, TCI_NR_ACTIVE_TRAVELERS) - トラフィック制御でアクティブな移動者の総数を返します。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER, num travelnr) - トラフィック制御でアクティブなn番目の移動者への参照を返します。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER_COUPLING, num travelernr) - トラフィック制御の変数ツリーに格納され、アクティブなn番目の移動者と関連付けられている結合ノードへの参照を返します。この結合を使用して、アクティブな移動者に関するカスタムユーザー情報を格納できます。このためには、nodeinsertinto()を使用して結合ノードにサブノードを追加する、データを追加するなどを行います。アクティブな移動者がトラフィック制御エリアを離れると、結合およびそのサブノードは自動的に破棄されることに注意してください。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER_RANK_FROM_TRAVELER, obj traveler) - このコマンドは移動者オブジェクトへの参照を取得し、トラフィック制御のアクティブな移動者のうち、どのインデックスがその移動者と関連付けられているかを返します。0が返された場合、そのオブジェクトはトラフィック制御内のアクティブな移動者ではありません。
trafficcontrolinfo(tc, TCI_NR_MEMBERS) - トラフィック制御エリアのメンバーであるネットワークノードの総数を返します。
trafficcontrolinfo(tc, TCI_MEMBER, num membernr) - トラフィック制御のn番目のネットワークノードメンバーへの参照を返します。
trafficcontrolinfo(tc, TCI_MEMBER_COUPLING, num membernr) - トラフィック制御の変数に格納され、トラフィック制御のn番目のネットワークノードメンバーと関連付けられている結合ノードへの参照を返します。TCI_ACTIVE_TRAVELER_COUPLINGと同様に、このノードを使用して、そのネットワークノードに関連するデータを格納できます。
trafficcontrolinfo(tc, TCI_MEMBER_RANK_FROM_NETWORK_NODE, obj netnode) - ネットワークノードの参照を取得し、トラフィック制御内における、そのネットワークノードのメンバーインデックスを返します。0が返された場合、そのネットワークノードはトラフィック制御のメンバーではありません。
trafficcontrolinfo(tc, TCI_NR_ENTRY_REQUESTS) - トラフィック制御エリアへの進入待ちキューに存在する進入リクエストの数を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_TRAVELER, num requestnr) - n番目の進入リクエストに関連付けられており、トラフィック制御エリアへの進入待ちである移動者への参照を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_NETWORK_NODE, num requestnr) - 移動者が待機しており、n番目の進入リクエストと関連付けられているネットワークノードへの参照を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_NODE, num requestnr) - n番目の進入リクエストに関連付けられているノードへの参照を返します。TCI_ACTIVE_TRAVELER_COUPLINGと同様に、サブノードを追加して、リクエストに関連するデータを格納できます。ただし、このノードのデータはトラフィック制御ロジックで使用されるため、変更してはいけません。
trafficcontrolinfo(tc, TCI_ALLOW_ENTRY, num requestnr) - このコマンドを呼び出すと、トラフィック制御に対して、n番目の進入リクエストと関連付けられている移動者のトラフィック制御エリアへの進入を許可するよう通知されます。
trafficcontrolinfo(tc, TCI_SET_ENTRY_REQUEST_RANK, num requestnr, num settorank) - このコマンドを呼び出すと、トラフィック制御はn番目の進入リクエストを指定されたrankにランク変更します。
また、トラフィック制御トリガーの使用に関連するノートは、トラフィック制御のデフォルトロジックに優先されます。トラフィック制御のOnEntryRequestトリガーは、移動者がトラフィック制御エリアへの進入を最初に要求したとき起動され、3つのいずれかの値を返します。
TC_ON_ENTRY_REQUEST_DEFAULT - トリガーからこの値が返された場合、トラフィック制御は通常のフィルタリングロジックを実行します。
TC_ON_ENTRY_REQUEST_ALLOW - この値が返された場合、トラフィック制御はデフォルトロジックを無視し、移動者がエリアに進入することを無条件で許可します。このオプションが使用されるとき、トラフィック制御は最大容量の変数を無視するため、定義されているロジックによっては、エリア内の移動者の数がトラフィック制御に指定した最大容量変数を超過する可能性があることに注意してください。
TC_ON_ENTRY_REQUEST_QUEUE - この値が返された場合、トラフィック制御はデフォルトロジックを無視し、リクエストをリクエストキューに追加して、その時点では移動者がエリアに進入することを許可しません。
トラフィック制御のOnExitトリガーは、2つの戻り値のどちらかを返します。
0 - この値が返された場合、トラフィック制御はデフォルトロジックを実行し、他の移動者に進入その他を許可します。
1 - この値が返された場合、トラフィック制御は何も行いません。この場合、ユーザーがトリガーを使用して、どの移動者が受け取るのかを、TCI_ALLOW_ENTRYを使用し、トラフィック制御に対して明示的に通知します。
移動者のエリア進入を許可するためカスタムロジックの実装を計画している場合は、トラフィック制御のデフォルトの「相互排除」モードを使用することをお勧めします。
trafficcontrolinfo(tc, TCI_NR_ACTIVE_TRAVELERS) - トラフィック制御でアクティブな移動者の総数を返します。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER, num travelnr) - トラフィック制御でアクティブなn番目の移動者への参照を返します。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER_COUPLING, num travelernr) - トラフィック制御の変数ツリーに格納され、アクティブなn番目の移動者と関連付けられている結合ノードへの参照を返します。この結合を使用して、アクティブな移動者に関するカスタムユーザー情報を格納できます。このためには、nodeinsertinto()を使用して結合ノードにサブノードを追加する、データを追加するなどを行います。アクティブな移動者がトラフィック制御エリアを離れると、結合およびそのサブノードは自動的に破棄されることに注意してください。
trafficcontrolinfo(tc, TCI_ACTIVE_TRAVELER_RANK_FROM_TRAVELER, obj traveler) - このコマンドは移動者オブジェクトへの参照を取得し、トラフィック制御のアクティブな移動者のうち、どのインデックスがその移動者と関連付けられているかを返します。0が返された場合、そのオブジェクトはトラフィック制御内のアクティブな移動者ではありません。
trafficcontrolinfo(tc, TCI_NR_MEMBERS) - トラフィック制御エリアのメンバーであるネットワークノードの総数を返します。
trafficcontrolinfo(tc, TCI_MEMBER, num membernr) - トラフィック制御のn番目のネットワークノードメンバーへの参照を返します。
trafficcontrolinfo(tc, TCI_MEMBER_COUPLING, num membernr) - トラフィック制御の変数に格納され、トラフィック制御のn番目のネットワークノードメンバーと関連付けられている結合ノードへの参照を返します。TCI_ACTIVE_TRAVELER_COUPLINGと同様に、このノードを使用して、そのネットワークノードに関連するデータを格納できます。
trafficcontrolinfo(tc, TCI_MEMBER_RANK_FROM_NETWORK_NODE, obj netnode) - ネットワークノードの参照を取得し、トラフィック制御内における、そのネットワークノードのメンバーインデックスを返します。0が返された場合、そのネットワークノードはトラフィック制御のメンバーではありません。
trafficcontrolinfo(tc, TCI_NR_ENTRY_REQUESTS) - トラフィック制御エリアへの進入待ちキューに存在する進入リクエストの数を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_TRAVELER, num requestnr) - n番目の進入リクエストに関連付けられており、トラフィック制御エリアへの進入待ちである移動者への参照を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_NETWORK_NODE, num requestnr) - 移動者が待機しており、n番目の進入リクエストと関連付けられているネットワークノードへの参照を返します。
trafficcontrolinfo(tc, TCI_ENTRY_REQUEST_NODE, num requestnr) - n番目の進入リクエストに関連付けられているノードへの参照を返します。TCI_ACTIVE_TRAVELER_COUPLINGと同様に、サブノードを追加して、リクエストに関連するデータを格納できます。ただし、このノードのデータはトラフィック制御ロジックで使用されるため、変更してはいけません。
trafficcontrolinfo(tc, TCI_ALLOW_ENTRY, num requestnr) - このコマンドを呼び出すと、トラフィック制御に対して、n番目の進入リクエストと関連付けられている移動者のトラフィック制御エリアへの進入を許可するよう通知されます。
trafficcontrolinfo(tc, TCI_SET_ENTRY_REQUEST_RANK, num requestnr, num settorank) - このコマンドを呼び出すと、トラフィック制御はn番目の進入リクエストを指定されたrankにランク変更します。
また、トラフィック制御トリガーの使用に関連するノートは、トラフィック制御のデフォルトロジックに優先されます。トラフィック制御のOnEntryRequestトリガーは、移動者がトラフィック制御エリアへの進入を最初に要求したとき起動され、3つのいずれかの値を返します。
TC_ON_ENTRY_REQUEST_DEFAULT - トリガーからこの値が返された場合、トラフィック制御は通常のフィルタリングロジックを実行します。
TC_ON_ENTRY_REQUEST_ALLOW - この値が返された場合、トラフィック制御はデフォルトロジックを無視し、移動者がエリアに進入することを無条件で許可します。このオプションが使用されるとき、トラフィック制御は最大容量の変数を無視するため、定義されているロジックによっては、エリア内の移動者の数がトラフィック制御に指定した最大容量変数を超過する可能性があることに注意してください。
TC_ON_ENTRY_REQUEST_QUEUE - この値が返された場合、トラフィック制御はデフォルトロジックを無視し、リクエストをリクエストキューに追加して、その時点では移動者がエリアに進入することを許可しません。
トラフィック制御のOnExitトリガーは、2つの戻り値のどちらかを返します。
0 - この値が返された場合、トラフィック制御はデフォルトロジックを実行し、他の移動者に進入その他を許可します。
1 - この値が返された場合、トラフィック制御は何も行いません。この場合、ユーザーがトリガーを使用して、どの移動者が受け取るのかを、TCI_ALLOW_ENTRYを使用し、トラフィック制御に対して明示的に通知します。
移動者のエリア進入を許可するためカスタムロジックの実装を計画している場合は、トラフィック制御のデフォルトの「相互排除」モードを使用することをお勧めします。
例
treenode netnode = trafficcontrolinfo(tc, TCI_MEMBER, 2);
オブジェクトデータ
オブジェクトへのアクセスとデータの割り当てを行うコマンド。
assertvariable (obj object, str variablename, num datatype)
オブジェクトの変数variablenameへの参照を取得します。変数が存在しない場合は作成します。
説明
このコマンドは、与えられた名前の変数への参照を返します。変数が存在しない場合、定義されたデータタイプで作成されます。
例
treenode newvar = assertvariable(Model.find("/Processor1"),"MyVariable", DATATYPE_NUMBER);
classobject (obj object)
インスタンスのクラスオブジェクトを返す
説明
インスタンスのクラスオブジェクトを返します。
例
if(classobject(current) == library().find("?Processor"))
{
pt("Processor1 is an instance of the Processor class.");pr();
}
currentがProcessorなら、出力コンソールにメッセージを表示します。
{
pt("Processor1 is an instance of the Processor class.");pr();
}
currentがProcessorなら、出力コンソールにメッセージを表示します。
contentunder (node thenode [, num objectsonly)
説明
このコマンドは、thenodeで指定されたノード内のツリーのノード数と、そのレイヤーから始まるサブツリーに含まれているノードの数の合計を返します。thenodeに他のノードが含まれていない場合、このコマンドは0を返します。objectsonlyが指定されていない、または0なら、FlexSimツリー内の任意のノードをthenodeとして渡すことができます。objectsonlyが0以外なら、オブジェクト以外のノードがthenodeとして渡された場合は0が返されます。
例
if (contentunder(current) >= getvarnum(current,"maxcontent"))
{
current.input.close;
}
currentの下に含まれているオブジェクトの数が、thisobjectdataにより参照されるオブジェクトのmaxcontentという変数と同じか、より大きい場合、currentの入力を閉じます。
{
current.input.close;
}
currentの下に含まれているオブジェクトの数が、thisobjectdataにより参照されるオブジェクトのmaxcontentという変数と同じか、より大きい場合、currentの入力を閉じます。
emptyfluidobject (obj object)
流体オブジェクトのコンテンツを0に設定する
説明
流体オブジェクトのコンテンツを0に設定します。
例
emptyfluidobject(current);
fluidcontent (obj fluidobject)
流体オブジェクトの現在の流体コンテンツを取得する
説明
指定されたfluidobjectの現在の流体コンテンツを返します。オブジェクトの「curcontent」変数を読み出すのと同じ動作です。離散オブジェクトが渡された場合、このコマンドは意味を持ちません。
例
double objcontent = fluidcontent(current.outObjects[1]);
fluidmaxcontent (obj fluidobject)
流体オブジェクトの最大の流体コンテンツを取得する
説明
指定されたfluidobjectに定義された最大の流体コンテンツを返します。オブジェクトの「maxcontent」変数を読み出すのと同じ動作です。離散オブジェクトが渡された場合、このコマンドは意味を持ちません。
例
double objmaxcontent = fluidmaxcontent(current.outObjects[1]);
getanimationvar (obj object, num/str animation, str varName)
アニメーション変数の現在の値を取得する
説明
アニメーション変数の現在の値を取得します。アニメーション変数の詳細については、setanimationvar()を参照してください。
例
treenode curItem = getanimationvar(current, "Animation1", "Item1");
getcreationtime (obj object)
フローアイテムが作成された時間を取得する
説明
フローアイテムが最初に作成された時間を返します。
例
time() - getcreationtime(item)
getentrytime (obj object)
フローアイテムが現在のオブジェクトに進入した時間を取得する
説明
アイテムの最後の入力時間(フローアイテムが最後に別のオブジェクトに進入した時間)を返します。
例
time() - getentrytime(item)
getframe (obj object)
オブジェクトに描画される現在の形状フレームを取得する
説明
オブジェクトについて描画される現在の3D形状フレームを返します。オブジェクトに割り当てられている3D形状がmyshape.3dsという名前で、myshape.3dsと同じディレクトリにmyshapeFRAME1.3dsおよびmyshapeFRAME2.3dsというファイル名の2つの追加3D形状が存在するなら、myshape.3dsがロードされると同時に、2つの追加ファイルが自動的にFlexSimにロードされ、オブジェクトのフレーム0、1、2の設定により、オブジェクトの形状が、3つのファイルにより定義されるそれぞれの形状に変更されます。
例
if(getframe(current) == 3)) setframe(current, 5);
getobjectshapeindex (obj object)
オブジェクトに割り当てられている3D形状のインデックス番号を取得する
説明
オブジェクトに現在割り当てられている3D形状のインデックス番号を返します。
例
getobjectshapeindex(item);
getobjecttextureindex (obj object)
オブジェクトの3D形状のテクスチャとして割り当てられている画像のインデックス番号を取得する
説明
オブジェクトの3D形状のデフォルトテクスチャとして現在割り当てられている、bmpまたはjpeg画像のインデックス番号を返します。
例
getobjecttextureindex(item);
getoutput (obj involved)
getvarnode (obj object, str/num var)
オブジェクトの変数へのノード参照を取得する
説明
指定されたオブジェクトの、指定された変数のノードへの参照を返します。
例
treenode schedule = getvarnode(current,"schedule");
getvarnum (obj object, str/num var)
オブジェクトの数値変数の値を取得する
説明
指定されたオブジェクトの、指定された変数に格納されている数値を返します。
例
double speed = getvarnum(current,"speed");
getvarstr (obj object, str/num var)
オブジェクトの文字列変数の値を取得する
説明
指定されたオブジェクトの、指定された変数に格納されている文字列データを返します。
例
pt(getvarstr(model().subnodes[2],"creationtrigger"));
isclasstype (obj object, num/str classtype)
objectをclasstypeと比較し、yesなら1、noなら0を返す
説明
オブジェクトが与えられたclasstypeかどうかを返します。1はyesを、0はnoを意味します。classtype に使用可能なパラメータは
CLASSTYPE_FLEXSIMOBJECT
CLASSTYPE_FIXEDRESOURCE
CLASSTYPE_TASKEXECUTER
CLASSTYPE_NETWORKNODE
などです。
CLASSTYPE_FLEXSIMOBJECT
CLASSTYPE_FIXEDRESOURCE
CLASSTYPE_TASKEXECUTER
CLASSTYPE_NETWORKNODE
などです。
例
isclasstype(current, CLASSTYPE_DISPATCHER);
reassignticker (obj fluidobject, obj ticker[, int resortticker])
流体オブジェクトのティッカーを再割り当てする
説明
最初のパラメータとして渡される流体オブジェクトを、現在のティッカーの制御から、2番目のパラメータとして渡されるティッカーの制御に変更します。その後でオブジェクトは、新しいティッカーのティック時間が経過するごとに流体移動が計算されます。互いに接続されている流体オブジェクトは、常に同じティッカーで制御することをお勧めします。resorttickerが1なら、新しいティッカーは制御対象オブジェクトのリストをただちに再ソートします。これにより、一部の流体オブジェクトの評価順序が変更され、モデルの動作に副作用が起きる可能性があります。
例
reassignticker(current,Model.find("Ticker2",1);
resumeanimation (obj object, num/str animation[, num resumeAtType, num resumeAtVal])
廃止、Animationクラスを使用すること
説明
このコマンドは廃止されました。代わりにAnimationクラスを使用してください。
アニメーションの中間のポイントから、アニメーションを再開します。
アニメーションの中間のポイントから、アニメーションを再開します。
例
resumeanimation(current, "Stand");
setanimationvar (obj object, num/str animation, str varName, num/obj toValue)
オブジェクトのアニメーション変数の値を設定する
説明
オブジェクトのアニメーション変数の値を設定します。アニメーション変数は、アニメーションのサロゲート、キーフレーム間の時間、与えられたキーフレームの場所/回転/サイズの値など、アニメーションを実行するごとに動的に変更の必要がある属性です。たとえば、アニメーションの構築にサロゲートを使用できます。このためには、アニメーションを作成するときFlowitem Binから、使用するデフォルトのビジュアルを選択します。その後でシミュレーションを実行するとき、これらのサロゲートについて実際のフローアイテムを代入します。この代入を行うには、そのサロゲートと関連付けたアニメーション変数の値を、フローアイテムへの実際の参照に設定します。別の例として、アニメーション変数を使用し、キーフレームのz位置を実行時に動的に定義できます。
例
setanimationvar(current, "Animation1", "Item1", current.first);
setframe (obj object, num/str toframe)
オブジェクトの形状フレームを設定する
説明
オブジェクトのframe属性を、framenumberに設定します。frameは表示する3D画像を定義します。これは、オブジェクトの3D形状をその場で変更するため便利な方法です。オブジェクトにフレームを定義する方法は2つあります。最初に、各種の3Dファイルの名前付けによってこの操作を行えます。たとえば、オブジェクトにデフォルト形状としてOperator.3dsが割り当てられ、Operator.3dsと同じディレクトリにOperatorFRAME1.3ds、OperatorFRAME2.3ds、OperatorFRAME3.3dsという名前の追加ファイルが存在する場合、frame属性を0、1、2、3に設定して、表示される形状をそれぞれの3dsファイルに変更できます。次に、オブジェクトのshape属性にサブノードを追加し、そのフレームに関連付けられている3Dファイルへのパスを各サブノードに持たせることができます。その場合、フレーム1はshape属性の最初のサブノードに、以後のフレームも同様に割り当てられます。これは、FlexSimの環境内で形状フレームを定義するため使用される手法です。toframeが文字列の場合、後者の方法をお勧めします。この場合、対応する名前を持つshape属性サブノードが探されます。このコマンドの用途の1つは、「壊れた」形状を表示するためOnDownトリガーの3D形状を変更することです。
例
if(getframe(current) == 3)) setframe(current, 5);
setobjectbillboard (obj object, num mode)
ビジュアルツールオブジェクトのbillboard属性を設定する
説明
このコマンドは、ビジュアルツールオブジェクトのbillboard属性を設定します。次のモードが利用可能です。
0:ビルボードなし、ビジュアルツールは回転の設定に基づいて表示されます。
1:垂直ビルボード(平面のみ)、モデル内で平面が垂直に立ち、同じビュー平面に沿って、常にカメラの方角を向きます。
2:全体ビルボード(平面のみ)、表示角度にかかわらず平面の表面が常に存在するようになります。
3:スクリーンロック済みビルボード、ビジュアルツールをビューの前面にロックします。
0:ビルボードなし、ビジュアルツールは回転の設定に基づいて表示されます。
1:垂直ビルボード(平面のみ)、モデル内で平面が垂直に立ち、同じビュー平面に沿って、常にカメラの方角を向きます。
2:全体ビルボード(平面のみ)、表示角度にかかわらず平面の表面が常に存在するようになります。
3:スクリーンロック済みビルボード、ビジュアルツールをビューの前面にロックします。
例
setobjectbillboard(current, 1);
setobjectshapeindex (obj object, num index)
オブジェクトの3D形状のインデックス番号を設定する
説明
オブジェクトの3D形状のインデックス番号を設定します。新しいインデックスを有効にするには、オブジェクトのshapeノードを削除するか、名前を変更する必要があるため、このコマンドはshapeノードの名前を「_shape」に変更します。インデックス番号は、現在インポートされている3D形状の有効なインデックス番号の必要があります。現在インポートされている3D形状を表示、および追加形状をインポートするには、[ビュー]->[メディアファイル]を使用します。オブジェクトの3D形状をその場で変更する別の方法として、setframe()を参照してください。
例
setobjectshapeindex(item,getshapeindex("fs3d\\Processor.3ds"));
setobjecttextureindex (obj object, num index)
オブジェクトの3D形状のテクスチャとして割り当てられている画像のインデックス番号を設定する
説明
オブジェクトの3D形状のテクスチャとして割り当てられている、bmpまたはjpeg画像のインデックス番号を設定します。インデックス番号は、現在インポートされているbmpまたはjpeg画像の有効なインデックス番号の必要があります。現在インポートされている画像を表示する、または別のbmpやjpeg画像をインポートするには、ツールボックスの[メディアをインポート]オプションを使用してください。このコマンドはオブジェクトのimageobject属性を変更しないため、モデルがリセットされると元のテクスチャに戻ることに注意してください。
例
setobjecttextureindex(item,gettextureindex("bitmaps\\flowitempicture.bmp"));
setresetposition (obj object)
オブジェクトのリセット位置を設定する
説明
objectのリセット位置を現在の位置に設定します。
例
setresetposition(current);
setvarnum (obj object, str/num var, num value)
オブジェクトの数値変数の値を設定する
説明
objectの指定された変数を、valueで渡された数値に設定します。
例
setvarnum(current.centerObjects[1],"speed",1.5);
setvarstr (obj object, str/num var, str value)
オブジェクトの文字列変数の値を設定する
説明
objectの指定された変数の文字列値を設定します。
例
setvarstr(current,"cycletime","return exponential(10,1);");
switch_enablestats (obj object[, num off/on])
オブジェクトの「stats」フラグを取得または設定する
説明
objectの「stats」フラグを取得または設定します。値が1なら有効に、0なら無効に設定し、-1なら現在の値を取得します。
例
switch_enablestats(so(),1)
switch_hideconnectors (obj object[, num off/on])
オブジェクトの「Hide Connectors」フラグを取得または設定する
説明
objectの「Hide Connectors」フラグを取得または設定します。値が1なら非表示、0なら表示に設定し、-1なら現在の値を取得します。コネクターを非表示にすると、オブジェクトへの入力と出力の両方について、ポートおよび接続の表示がオフになります。ビューウィンドウにはhideallconnectorsという名前の属性があり、ビュー内のすべてのオブジェクトについてコネクターの表示をコントロールすることに注意してください。
例
switch_hideconnectors(so(),1)
switch_hidecontents (obj object[, num off/on])
オブジェクトの「Show Contents」フラグを取得または設定する
説明
objectの「Show Contents」フラグを取得または設定します。値が1なら非表示、0なら表示に設定し、-1なら現在の値を取得します。オブジェクトのコンテンツを非表示にすると、その中に含まれているオブジェクト(例:フローアイテム)が表示されなくなります。
例
switch_hidecontents(so(),1)
switch_hidelabel (obj object[, num off/on])
オブジェクトの「Show Name」フラグを取得または設定する
説明
objectの「Show Name」フラグを取得または設定します。値が1なら、オブジェクトの名前と統計情報を画面に表示しません。値が0なら、ビューウィンドウのviewhidealllabels属性に応じて、オブジェクトの名前と、多くの場合は統計情報を表示します。値が-1なら、スイッチの現在の値を取得します。ビューウィンドウのviewhidealllabels属性は次の値のいずれかで、ウィンドウ内のすべてのオブジェクトについてラベル表示に適用されます。0=名前と統計情報を表示、1=名前と統計情報を非表示、2=名前のみを表示。
例
switch_hidelabel(so(),1)
switch_hideshape (obj object[, num off/on])
オブジェクトの「Show 3D Shape」フラグを取得または設定する
説明
objectの「Show 3D Shape」フラグを取得または設定します。値が1なら非表示、0なら表示、-1なら現在の値を取得します。ビューウィンドウにはhidealldrawcontentという名前の属性もあり、ビュー内のすべてのオブジェクトについて3D形状の表示をコントロールすることに注意してください。
例
switch_hideshape(so(),1)
switch_showobject (obj object[, num off/on])
オブジェクトノードのオブジェクトデータを展開/折りたたみする
説明
ツリービューのオブジェクトノードのオブジェクトデータを展開または折りたたみします。これは、ツリービューでオブジェクトの[>次へ]をクリックするのと同様の操作です。値が1なら展開、0なら折りたたみ、-1なら現在の値を取得します。
例
switch_showobject(so(),1)
updatelocations (obj object)
オブジェクト、およびその中にあるオブジェクトの場所を更新する
説明
このコマンドは、オブジェクト自身、およびその中にあるオブジェクトの場所を更新します。このコマンドを使用して、クエリの実行や、オブジェクトの場所を照会する機能を実行する前に、場所を更新できます。この関数にフローアイテムをオブジェクトとして渡すことはできません。
例
updatelocations(current);
updatestate (obj object [, num profilenr])
オブジェクトの状態を更新する
説明
指定されたオブジェクトの状態を更新します。モデルの実行中に、オブジェクトのOnDraw関数で状態を円滑に表示するため使用できます。
例
updatestate(current);
オブジェクト関数
オブジェクトやノードの関数呼び出しに関係するコマンドで、ノード関数、イベント、メッセージ、およびそれらに関連するアクセス変数が含まれます。
c <括弧なし>
説明
このコマンドは、関数の実行中にアクティブノードを参照するため使用されます。関数がnodefunction()を使用して呼び出された場合、cは関数が書き込まれているノードへの参照を返します。関数がイベント関数なら、cはイベントを含むオブジェクトへの参照を返します。
例
treenode current = ownerobject(c);
debug ([num operation, num/obj p2, num/obj p3])
Flexscriptでデバッグを開始するブレイクポイントとして機能する
説明
開発者向けです。このコマンドは、Flexscriptのステップデバッガーをコントロールするため使用されます。このコマンドをパラメータなしで呼び出すと、コードのその行にブレイクポイントが存在するかのように動作します。
operationは次のいずれかです。
DEBUG_STOP 0
DEBUG_STEP 1
DEBUG_CONTINUE 2
DEBUG_IS_STOPPED 3
DEBUG_GET_LINE_NR 4
DEBUG_DUMP_VARIABLES 5
DEBUG_STOP_SIMULATION 6
DEBUG_REFRESH_BREAK_POINTS 7
DEBUG_ADD_BREAK_POINT 8
DEBUG_DELETE_BREAK_POINT 9
DEBUG_GET_WATCH_VARIABLE 10
DEBUG_ENABLE_CODE_PROFILING 11
DEBUG_PRINT_CODE_PROFILING_INFO 12
DEBUG_RESET_CODE_PROFILING 13
operationは次のいずれかです。
DEBUG_STOP 0
DEBUG_STEP 1
DEBUG_CONTINUE 2
DEBUG_IS_STOPPED 3
DEBUG_GET_LINE_NR 4
DEBUG_DUMP_VARIABLES 5
DEBUG_STOP_SIMULATION 6
DEBUG_REFRESH_BREAK_POINTS 7
DEBUG_ADD_BREAK_POINT 8
DEBUG_DELETE_BREAK_POINT 9
DEBUG_GET_WATCH_VARIABLE 10
DEBUG_ENABLE_CODE_PROFILING 11
DEBUG_PRINT_CODE_PROFILING_INFO 12
DEBUG_RESET_CODE_PROFILING 13
例
debug();
delayednodefunction (node thenode, double timeDelay[, par1, par2, ... par10])
説明
開発者向けです。このコマンドは、thenodeに定義されている関数を、定義された遅延時間の後で実行します。nodefunction()コマンドと同様ですが、与えられた遅延時間だけノードの起動を遅延する点が異なります。
例
delayednodefunction(current.myFunc, tonum(item));
eventlisten (obj object, str eventName, node relayNode[, num flags, par1, par2, ... par10])
説明
このコマンドはリスニングメカニズムを作成し、定義されたイベントがオブジェクトで呼び出されると、relayNodeも実行されるようにします。flagsは次に示す値のいずれかのビット単位マスクです。
オブジェクトでリッスンできるイベントのリストを取得するには、function_s(object, "enumerateEvents", destNode)を呼び出します。オブジェクトがdestNodeにダンプするテーブルには、そのオブジェクトでリッスンできるすべてのイベントに関する情報が含まれています。
一部のイベントには「要件」が存在します。そのイベントを正しくバインドするには、追加パラメータを渡す必要があります。列挙テーブルには、要件の数とそれらの名前についての情報が含まれています。要件が必要な場合、par1、par2などに置き換わり、パラメータの順序がずれることになります。たとえば、イベントに2つの要件が存在する場合、それらの要件がeventlisten()呼び出しのpar1とpar2を占め、par3がrelayNodeのコードでparam(1)になります。
EVENT_PRE_LISTEN:リスニング関数は、theNodeより前に呼び出されます。
EVENT_LISTEN:(デフォルト)リスニング関数は、theNodeの後で呼び出されます。
EVENT_PERSIST:リスナーは、モデルがリセットされても継続します。
EVENT_PASS_THROUGH_PARAMS:theNodeが呼び出されるときイベントに渡されるパラメータは、リスニングノードにも「引き継ぎ」で渡されます。この場合、par1、par2などのパラメータは使用されません。
EVENT_LISTEN_ONCE:最初のイベントが起動した後で、リスニングメカニズムは自動的に削除されます。
リスニングノードが呼び出され、EVENT_STOP_LISTENINGを返した場合、リスナーメカニズムは削除され、それ以後リスニングノードは呼び出されません。戻り値は、リスニングに関連付けられているノードへの参照です。このノードが後で削除されると、リスニングメカニズムは停止します。オブジェクトでリッスンできるイベントのリストを取得するには、function_s(object, "enumerateEvents", destNode)を呼び出します。オブジェクトがdestNodeにダンプするテーブルには、そのオブジェクトでリッスンできるすべてのイベントに関する情報が含まれています。
一部のイベントには「要件」が存在します。そのイベントを正しくバインドするには、追加パラメータを渡す必要があります。列挙テーブルには、要件の数とそれらの名前についての情報が含まれています。要件が必要な場合、par1、par2などに置き換わり、パラメータの順序がずれることになります。たとえば、イベントに2つの要件が存在する場合、それらの要件がeventlisten()呼び出しのpar1とpar2を占め、par3がrelayNodeのコードでparam(1)になります。
例
eventlisten(current, "OnEntry", current.entrylistener);
executefsnode (node thenode, node c[, node i, node/num/str eventdata, int nobuild])
ノードをFlexscriptとして実行する
説明
ノードをFlexscriptとして動的に実行します。ノードがまだFlexscriptでない場合、nobuildパラメータを0にします。文字列データをFlexscriptとして解析して実行するもので、たとえばグローバルテーブルやラベルから使用します。cおよびiパラメータは、関数内でcおよびiとしてアクセスできます。eventdataは、文字列であればeventdataとして、数値であればeventcode(整数)としてアクセスできます。eventdataがノードであれば、関数内でtonode(eventdata)を使用してアクセスできます。
例
executefsnode(current.labels["myFunc"],NULL,NULL,NULL,0)
currentのmyFuncラベルにあるスクリプトを実行し、関数のc、i、eventdataにNULLを渡します。
currentのmyFuncラベルにあるスクリプトを実行し、関数のc、i、eventdataにNULLを渡します。
i <括弧なし>
説明
開発者向けです。このコマンドは、イベント関数でのみ使用されます。値として渡されたオブジェクトを参照するために使用されます。値が0なら、コマンドが関連オブジェクトです。
例
string involvedname = i.name;
involvednameを、値として渡されたオブジェクトの名前に設定します。値が0なら、関連オブジェクトとします。
involvednameを、値として渡されたオブジェクトの名前に設定します。値が0なら、関連オブジェクトとします。
inheritcode ()
説明
開発者向けです。このコマンドは、サブクラス関数の継承に使用されます。イベント関数でこれを呼び出すと、オブジェクトのclassobjectで同じイベント関数が呼び出されます。C++またはDLLコードでは、_inheritcode(callpoint);を呼び出します。
例
Flexscript: inheritcode();
C++またはDLL: _inheritcode(callpoint);
C++またはDLL: _inheritcode(callpoint);
ip <括弧なし>
説明
開発者向けです。「関連ポート」を意味するノードポインター。「eventdata」のエイリアスです。
例
msgparam (num param)
OnMessageトリガー内でメッセージパラメータの値を取得する
説明
sendmessage()またはsenddelayedmessage()コマンドで渡されたパラメータを返します。OnMessageトリガーでのみ使用されます。
例
int msgtype = msgparam(1);
treenode item = msgparam(2);
Array data = msgparam(3);
treenode item = msgparam(2);
Array data = msgparam(3);
msgsendingobject ()
OnMessageトリガー内で、メッセージを送信するオブジェクトへの参照を取得する
説明
sendmessage()またはsenddelayedmessage()コマンドで定義された、メッセージを送信したオブジェクトへの参照を返します。OnMessageトリガーでのみ使用されます。
例
treenode sender = msgsendingobject;
nodefunction (node thenode [, par1, par2, ... par10])
説明
開発者向けです。このコマンドは、thenodeに定義されている関数を実行します。thenodeはC++ノードまたはFlexscriptノードとして切り替える必要があります。ノードがC++の場合、このコマンドを呼び出す前にモデルをコンパイルする必要があります。関数に渡す必要のあるパラメータは、par1、par2などで渡します。最大10までのパラメータを渡すことができます。このコマンドを使用して渡される値はすべて数値ですが、呼び出された関数内でparam(x)コマンドを使用してアクセスおよび再キャストできます。xはパラメータの数です。
例
nodefunction(node_v_entrytrigger,tonum(item),portnum);
nodefunctionlisten (node theNode, node relayNode[, num flags, par1, par2, ... par10])
説明
開発者向けです。このコマンドはリスニングメカニズムを作成し、theNodeでnodefunction()が呼び出されると、relayNodeも実行されるようにします。flagsは次に示す値のいずれかのビット単位マスクです。
NFL_PRE_LISTEN:リスニング関数は、theNodeより前に呼び出されます。
NFL_LISTEN:(デフォルト)リスニング関数は、theNodeの後で呼び出されます。
NFL_PERSIST:リスナーは、モデルがリセットされても継続します。
NFL_PASS_THROUGH_PARAMS:theNodeが呼び出されるとき、この関数に渡されるパラメータは、リスニングノードにも「引き継ぎ」で渡されます。この場合、par1、par2などのパラメータは使用されません。
リスニングノードが呼び出され、NFL_STOP_LISTENINGを返した場合、リスナーメカニズムは削除され、それ以後リスニングノードは呼び出されません。戻り値は、リスニングに関連付けられているノードへの参照です。このノードが後で削除されると、リスニングメカニズムは停止します。例
nodefunctionlisten(getvarnode(current, "entrytrigger"), current.entrylistener);
param (num index)
関数に渡されるパラメータを取得する
説明
このコマンドは、nodefunction()コマンドにより呼び出される関数の内部で使用されます。インデックスによりノード(またはツリーノード)、string、int、double、stringarray、intarray、doublearray、treenodearrayのいずれかとして指定され、nodefunctionに渡されたパラメータを返します。nodefunction()に渡される最初の追加パラメータはパラメータ1、2番目はパラメータ2の順に番号が付けられます。
例
トリガー/フィールドは
nodefunction(thefuncnode, item)
で呼び出された場合、トリガー/フィールド内で、最初の追加パラメータとして渡されたアイテムへのアクセスは
treenode item = param(1);
で取得されます。他の例として、次のものがあります。
double quantity = param(2);
var value = param(1); // この例ではどのようなタイプの値も使用できます
nodefunction(thefuncnode, item)
で呼び出された場合、トリガー/フィールド内で、最初の追加パラメータとして渡されたアイテムへのアクセスは
treenode item = param(1);
で取得されます。他の例として、次のものがあります。
double quantity = param(2);
var value = param(1); // この例ではどのようなタイプの値も使用できます
parqty ()
説明
開発者向けです。nodefunctionに渡されたパラメータの数を取得します。この関数は、nodefunctionコマンドとともに使用されます。返される値はFlexscriptの使用時にのみ適用され、C++では適用されません。
例
parqty()
selectall ()
説明
開発者向けです。モデル内のすべてのオブジェクトを選択します。
例
selectall()
senddelayedmessage (obj toobject, num delaytime, obj fromobject [, num par1, num par2, num par3])
遅延時間の経過後にオブジェクトに遅延メッセージを送信し、OnMessageトリガーを起動する
説明
delaytimeの経過後に、fromobjectからtoobjectにメッセージ送信を引き起こします。toobjectがメッセージを受信すると、OnMessageトリガーが起動します。
OnMessageトリガーのコードでは、fromobjectをmsgsendingobjectとして参照でき、parで渡された3つの数値をmsgparam(1)、msgparam(2)、msgparam(3)として参照できます。
このコマンドは、モデルの実行時に独自のタイムイベントを作成するため非常に便利です。
OnMessageトリガーのコードでは、fromobjectをmsgsendingobjectとして参照でき、parで渡された3つの数値をmsgparam(1)、msgparam(2)、msgparam(3)として参照できます。
このコマンドは、モデルの実行時に独自のタイムイベントを作成するため非常に便利です。
例
senddelayedmessage(current.outObjects[1], 25, current, 0, 0, 0);
このコマンドが実行されてから25時間単位後に、currentオブジェクトから、currentオブジェクトの出力ポート1に接続されているオブジェクトへメッセージを送信します。3つのユーザー定義パラメータにはすべて0が渡されます。
このコマンドが実行されてから25時間単位後に、currentオブジェクトから、currentオブジェクトの出力ポート1に接続されているオブジェクトへメッセージを送信します。3つのユーザー定義パラメータにはすべて0が渡されます。
sendmessage (obj toobject, obj fromobject [, var par1, var par2, var par3])
オブジェクトにメッセージを送信し、OnMessageトリガーを起動する
説明
直接関数呼び出しと同様に、fromobjectからtoobjectにメッセージをただちに送信します。toobjectがメッセージを受信すると、OnMessageトリガーが起動します。
OnMessageトリガーのコードでは、fromobjectをmsgsendingobjectとして参照でき、parで渡された3つの値をmsgparam(1)、msgparam(2)、msgparam(3)として参照できます。これらのメッセージパラメータはバリアントで、数値、文字列、ツリーノードの参照、配列を使用できます。
OnMessageトリガーのコードでは、fromobjectをmsgsendingobjectとして参照でき、parで渡された3つの値をmsgparam(1)、msgparam(2)、msgparam(3)として参照できます。これらのメッセージパラメータはバリアントで、数値、文字列、ツリーノードの参照、配列を使用できます。
例
sendmessage(current.centerObjects[1], current, item, 10);
currentの最初のセンターポートに接続されているオブジェクトにメッセージを送信します。アイテムへの参照をpar1、数値10をpar2として渡します。
currentの最初のセンターポートに接続されているオブジェクトにメッセージを送信します。アイテムへの参照をpar1、数値10をpar2として渡します。
thisclass <括弧なし>
説明
開発者向けです。このキーワードは、呼び出しを受信するオブジェクトのクラスを取得するため、eventfunctionで使用されます。
例
thisclass
オブジェクトポート
オブジェクトのポート接続に関連するコマンド。
closeallip (obj object)
オブジェクトのすべての入力ポートを閉じる
説明
オブジェクトのすべての入力ポートを閉じます。オブジェクトのすべての入力ポートを閉じると、オブジェクトへの進入がブロックされます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはcloseinput()およびstopinput()で参照されます。
例
closeallip(current)
closeallop (obj object)
オブジェクトのすべての出力ポートを閉じる
説明
オブジェクトのすべての出力ポートを閉じます。オブジェクトのすべての出力ポートを閉じると、オブジェクトからの退出がブロックされます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはcloseoutput()およびstopoutput()で参照されます。
例
closeallop(current)
closeip (obj object, num inputportnum)
オブジェクトの1つの入力ポートを閉じる
説明
オブジェクトのinputportnumだけを閉じます。オブジェクトの入力ポートを閉じると、そのポートからオブジェクトへの進入がブロックされます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはcloseinput()およびstopinput()で参照されます。
例
closeip(current,1)
closeop (obj object, num outputportnum)
オブジェクトの1つの出力ポートを閉じる
説明
オブジェクトのoutputportnumだけを閉じます。オブジェクトの出力ポートを閉じると、オブジェクトからそのポートへの退出がブロックされます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはcloseoutput()およびstopoutput()で参照されます。
例
closeop(current,1)
cpcpno (obj object, num port)
説明
このコマンドは、objectの指定されたセンターポート番号に接続されているセンターポート番号を返します。
例
int otherport = cpcpno(current,1);
otherportを、currentの最初のセンターポートが接続されている先のポートの番号に設定します。
otherportを、currentの最初のセンターポートが接続されている先のポートの番号に設定します。
inputopen (obj object)
オブジェクトの入力が開いていれば1を、開いていなければ0を返す
説明
オブジェクトの入力が開いていれば1を、開いていなければ0を返します。closeinput()、stopinput()、openinput()、resumeinput()コマンドは、このコマンドの戻り値に影響を及ぼします。closeip()やcloseallip()などのコマンドは戻り値に影響しません。
例
if(inputopen(current)) current.input.close;
ipavailable (obj object, num inputportnum)
説明
上流のオブジェクトが、指定されたオブジェクトの入力ポートを経由して利用可能なら、1を返します。具体的には、上流のオブジェクトが存在するか、停止しているか、出力が開いているか、接続されている出力ポートが開いているかをチェックします。この関数は、上流のオブジェクトが利用不能な場合は0を返します。
例
ipavailable(current,1)
ipopen (object object, num inputportnum)
説明
objectのinputportnumが開いていれば1を返します。開いていない場合、0を返します。
例
ipopen(current,1)
ipopno (obj object, num inputportnum)
objectのinputportnumに接続されている出力ポート番号
説明
このコマンドは、objectのinputportnumに接続されている出力ポート番号を返します。
例
int otherport = ipopno(current,1);
otherportを、currentオブジェクトの最初の入力ポートが接続されている先の出力ポートのポート番号に設定します。
otherportを、currentオブジェクトの最初の入力ポートが接続されている先の出力ポートのポート番号に設定します。
ipready (obj object, num inputportnum)
説明
オブジェクトのinputportnumが開いており、接続している他のオブジェクトの出力ポートも開いているなら1を返します。それ以外の場合、0を返します。このコマンドでは、このオブジェクトの入力や、接続先オブジェクトの出力が現在開いているかどうかは考慮されません。
例
ipready(current,1)
numconnections ()
現在アクティブなサーバー接続の数を取得する
説明
現在アクティブなサーバー接続の数を返します。
例
int numconns = numconnections();
変数numconnsを、現在アクティブなサーバー接続の数に設定します。
変数numconnsを、現在アクティブなサーバー接続の数に設定します。
opavailable (obj object, num outputportnum)
説明
下流のオブジェクトが、指定されたオブジェクトの出力ポートを経由して利用可能なら、1を返します。正確には、下流のオブジェクトが存在するか、停止しているか、入力が開いているか、接続されている入力ポートが開いているかをチェックします。この関数は、下流のオブジェクトが利用不能な場合は0を返します。
例
opavailable(current,1)
openallip (obj object)
オブジェクトのすべての入力ポートを開く
説明
objectのすべての入力ポートを開きます。結果として入力ポートがパススルー状態(接続されている両方のポートが開いている)になった場合、双方のオブジェクトに対してポートが「準備完了」になったことを示す通知メッセージが送信されます。入力ポートを持つオブジェクトはOnInOpenメッセージを、出力ポートを持つオブジェクトはOnOutOpenメッセージを受信します。ポートの走査のとき、各ポートでは1回だけパススルー評価を行えます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはopeninput()およびresumeinput()で参照されます。
例
openallip(current)
openallop (obj object)
オブジェクトのすべての出力ポートを開く
説明
objectのすべての出力ポートを開きます。結果として出力ポートがパススルー状態(接続されている両方のポートが開いている)になった場合、双方のオブジェクトに対してポートが「準備完了」になったことを示す通知メッセージが送信されます。入力ポートを持つオブジェクトはOnInOpenメッセージを、出力ポートを持つオブジェクトはOnOutOpenメッセージを受信します。ポートの走査のとき、各ポートでは1回だけパススルー評価を行えます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはopenoutput()およびresumeoutput()で参照されます。
例
openallop(current)
openip (obj object, num inputportnum)
オブジェクトの1つの入力ポートを開く
説明
objectのinputportnumだけを開きます。オブジェクトの入力ポートを開くと、そのポートからオブジェクトへの進入が許可されます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはopeninput()およびresumeinput()で参照されます。
例
openip(so(),1)
openop (obj object, num outputportnum)
オブジェクトの1つの出力ポートを開く
説明
objectのoutputportnumだけを開きます。オブジェクトの出力ポートを開くと、オブジェクトからそのポートへの退出が許可されます。モデラーは、流体オブジェクトを操作するときのみこのコマンドを使用します。離散オブジェクトの内部動作はポートの開閉をコントロールするため、このコマンドはオーバーライドされることがあります。離散オブジェクトの場合、モデラーはopenoutput()およびresumeoutput()で参照されます。
例
openop(so(),1)
opipno (obj object, num outputportnum)
objectのoutputportnumに接続されている入力ポート番号
説明
このコマンドは、objectのoutputportnumに接続されている入力ポート番号を返します。
例
int otherport = opipno(current,1);
otherportを、currentの最初の出力ポートが接続されている先の入力ポートの番号に設定します。
otherportを、currentの最初の出力ポートが接続されている先の入力ポートの番号に設定します。
opopen (obj object, num outputportnum)
説明
objectのoutputportnumが開いていれば1を返します。開いていない場合、0を返します。
例
opopen(current,1)
opready (obj object, num outputportnum)
説明
objectのoutputportnumが開いており、接続している他のオブジェクトの出力ポートも開いているなら1を返します。それ以外の場合、0を返します。このコマンドでは、このオブジェクトの出力や、接続先オブジェクトの入力が現在開いているかどうかは考慮されません。
例
opready(current,1)
outputopen (obj object)
オブジェクトの出力が開いていれば1を、開いていなければ0を返す
説明
オブジェクトの出力が開いていれば1を、開いていなければ0を返します。closeoutput()、stopoutput()、openoutput()、resumeoutput()コマンドは、このコマンドの戻り値に影響を及ぼします。closeop()やcloseallop()などのコマンドは戻り値に影響しません。
例
if(outputopen(current)) current.output.close;
currentオブジェクトの出力が開いているなら、出力を閉じます。
currentオブジェクトの出力が開いているなら、出力を閉じます。
transitionport ()
説明
モデル内のオブジェクトが最も最近に通過したポート番号を取得します。これは、モデルの実行で発生した最後のmoveobject()呼び出しを指します。
例
transitionport()
出力
デバッグやレポートの目的でモデラーにフィードバックを送るためのコマンド。
endoffile ()
現在開いているファイルの末尾に到達した場合に1を返す
説明
現在開いているファイルの末尾に到達した場合に1を返します。fileopen()とともに使用されます。
例
while(!endoffile()){string nextline = filereadline();}
fileclose ()
FlexSimファイルインターフェイスを閉じる
説明
FlexSimファイルインターフェイスを閉じ、ファイルが開いていた間に書き込まれたデータを保存します。
例
fileclose()
fileexists (str filepath)
ファイルが存在するなら1を、存在しなければ0を返す
説明
ファイルが存在するなら1を、存在しなければ0を返します。
例
if(fileexists("C:/myfile.txt"))
{
fileopen("C:/myfile.txt");
fpt("Hello World");
fileclose();
}
{
fileopen("C:/myfile.txt");
fpt("Hello World");
fileclose();
}
fileopen (str filename [, str opentype])
FlexSimファイルインターフェイスを開く
説明
FlexSimファイルインターフェイスを開きます。成功した場合は1を返します。エラーが発生した場合は0を返します。
パラメータ2は書き込みなら「w」、読み取りなら「r」、追記なら「a」です。デフォルトは「w」です。開いたテキストファイルに書き込むには、fpt()、fpr()、fpf()などのコマンドを使用します。ファイルから行を読み取るには、filereadline()を使用します。このコマンドを使用して同時に開けるファイルは1つだけです。複数のファイルを同時に開くには、C標準のfopen/fcloseコマンド、C++標準のfstreamクラス、またはdllを使用してください。
書き込みモードでは、ファイルのコンテンツがクリアされ、ファイルポインターがファイルの先頭に設定されます。ファイルに書き込まれたデータを保存するには、ファイルを閉じる必要があります。
パラメータ2は書き込みなら「w」、読み取りなら「r」、追記なら「a」です。デフォルトは「w」です。開いたテキストファイルに書き込むには、fpt()、fpr()、fpf()などのコマンドを使用します。ファイルから行を読み取るには、filereadline()を使用します。このコマンドを使用して同時に開けるファイルは1つだけです。複数のファイルを同時に開くには、C標準のfopen/fcloseコマンド、C++標準のfstreamクラス、またはdllを使用してください。
書き込みモードでは、ファイルのコンテンツがクリアされ、ファイルポインターがファイルの先頭に設定されます。ファイルに書き込まれたデータを保存するには、ファイルを閉じる必要があります。
例
fileopen("C:/myfile.txt", "w");
filereadline ()
現在開いているファイルから行を読み取る
説明
現在開いているファイルから行を読み取ります。fileopen()とともに使用されます。
例
string nextline = filereadline();
fpc (num value)
開いているファイルにASCII文字を書き込む
説明
開いているファイルにASCII文字を書き込みます。一般的な値には次のものがあります:TAB = 9、LF = 10、CR = 13
例
fpc(9)
fpd (num value)
開いているファイルに整数値を書き込む
説明
開いているファイルに整数値を書き込みます。浮動小数点数値は切り捨てられます。
例
fpd(3)は3を書き込みます。
fpd(3.23)は3を書き込みます。
fpd(3.954)は3を書き込みます。
fpd(4)は4を書き込みます。
fpd(3.23)は3を書き込みます。
fpd(3.954)は3を書き込みます。
fpd(4)は4を書き込みます。
fpf (num value)
開いているファイルに浮動小数点数値を書き込む
説明
開いているファイルに浮動小数点数値を書き込みます。
例
fpf(1.234)
fpr ()
開いているファイルに復帰(改行)を書き込む
説明
開いているファイルに復帰(改行)を書き込みます。
例
fpr()
fpt (str text)
開いているファイルに文字列を書き込む
説明
開いているファイルに文字列を書き込みます。
例
fpt("Hello")
mpd (num value)
システムコンソールに整数を表示する
説明
システムコンソールに整数値を書き込みます。
例
mpd(6);
mpf (num value)
システムコンソールに浮動小数点数値を表示する
説明
システムコンソールに浮動小数点数値を表示します。
例
mpf(7.69);
mpr ()
システムコンソールに改行を出力する
説明
システムコンソールに改行を出力します。
例
mpr();
mpt (str printvalue)
システムコンソールにテキストを表示する
説明
システムコンソールにテキストprintvalueを表示します。
例
mpt("System console printout");
outputtreecontent (node containernode, str path+filename)
containernodeの下にあるツリーのすべてのノードに含まれるデータを、テキストファイルに書き込む
説明
containernodeの下にあるツリーのすべてのノードに含まれるデータを、ディスク上のテキストファイルに書き込みます。ファイルが存在しなければ、作成されます。機能の詳細については、[統計]|[モデルドキュメント]メニューオプションを使用してください。
例
outputtreecontent(model(),"C:/MyModelDocumentation.txt")
print ([var value, var value2, ...])
与えられたパラメータの内容と改行をコンソールに表示する
説明
このコマンドには、0~20個のバリアントをパラメータとして使用できます。それぞれのパラメータは、スペースで区切ってコンソールに表示されます。すべてのパラメータが表示された後で、改行文字がコンソールに出力されます。書き込みを行う出力コンソールは開いている必要があります。コンソールを開くには、メニューの[デバッグ] > [出力コンソール]を使用します。
例
print("Number:", 1); print([1, 2]);
出力コンソールの別々の行に、「Number: 1」と「Array[2]: {1,2}」を表示します。
出力コンソールの別々の行に、「Number: 1」と「Array[2]: {1,2}」を表示します。
profileevents ()
現在イベントキューに存在するすべてのイベントの説明を出力コンソールに表示する
説明
現在イベントキューで待機中のすべてのイベントについて、説明を出力コンソールに表示します。書き込みを行う出力コンソールは開いている必要があります。コンソールを開くには、[ビュー]|[出力コンソール]メニューを使用します。
例
profileevents()
report (obj containerobj, str path+filename, num append [0/1])
説明
開発者向けです。containerobjの下に存在し、現在選択されているすべてのオブジェクトについて、「カンマ区切り値」(csv)形式の標準レポートファイルを生成します。appendが1なら、レポートは指定されたファイルの末尾に追記されます。appendが0なら、レポートを書き込む前にファイルが作成されるか、すでに存在するファイルが消去されます。
例
report(model());
reportmode (int mode [0=general, 1=state])
説明
開発者向けです。レポートモードを設定します(generalまたはstate)。
例
reportmode(0);
人
getactiverole (treenode person)
説明
人のアクティブな役割を返します。
例
getactiverole(token.Person)
getcensus ([obj model/group/location])
説明
モデル、場所グループ、個別の場所に存在する人の数を取得する
例
int census = getcensus(Group("PodA"));
getnumpeopleresources (obj group [, num availability{0=available/1=acquired}, num priority])
説明
ピープルリソースグループで利用可能な/取得済みのオブジェクトの数を取得します。priority値が渡された場合、その優先度のリクエストがリソースをプリエンプトできる場合も、リソースは利用可能と見なされます。
例
int numAvailable = getnumpeopleresources(Group("PodA"));
getpeopleresourceutilization (obj object/group[, num mode{0=ByState/1=ByAcquires}])
説明
人オブジェクトの使用率割合、またはピープルグループのすべてのメンバーの平均値を返します。
例
double utilization = getpeopleresourceutilization(Group("PodA"));
reacquirepreemptedresource (node token, node instance, node preemptedObject, node info, node activeProcess, num sameAsLast [, num newPriority])
説明
例
reacquirepreemptedresource(token, current, preemptedObject, info, activeProcess);
shiftscheduledownfunction (node downBehavior, node table, node downObject, double duration)
説明
例
shiftscheduledownfunction(lunch, shiftSchedule1, doctor, 400);
処理フロー
createtoken (obj instanceObject, obj/str activity, int start)
executesubflow (obj/str processFlow [, obj instanceObject, str startActivity, str finishActivity])
説明
処理フローのサブフローに、そのサブフローを開始するトークンを作成します。作成されたトークンがFinish Activityに到達すると、[戻り値]フィールドから評価された値を返します。
instanceObject:instanceObjectが指定された場合、サブフローのアクティビティで、instanceObjectにアクセスするためcurrentを使用できます。この機能は、複数のオブジェクトが同じサブフローを実行しながら、オブジェクト固有のデータを必要とする場合に便利です。
Start Activityが指定されていない場合、サブフローのアクティビティが検索され、最初のStart Activityが使用されます。
サブフローに複数のFinish Activityが含まれている場合、トークンが到達したFinish Activityから戻り値が評価されます。ただし、内部的なサブフローにより他のトークンがFinish Activityに到達する場合、正しい戻り値が評価されるようにFinish Activity名を指定することが必要な場合があります。
注:サブフローで使用されるアクティビティが遅延や待機を引き起こさないことが重要です。トークンが遅延や待機で中断された場合、executesubflow関数の終了時にトークンがFinish Activityに到達しません。
instanceObject:instanceObjectが指定された場合、サブフローのアクティビティで、instanceObjectにアクセスするためcurrentを使用できます。この機能は、複数のオブジェクトが同じサブフローを実行しながら、オブジェクト固有のデータを必要とする場合に便利です。
Start Activityが指定されていない場合、サブフローのアクティビティが検索され、最初のStart Activityが使用されます。
サブフローに複数のFinish Activityが含まれている場合、トークンが到達したFinish Activityから戻り値が評価されます。ただし、内部的なサブフローにより他のトークンがFinish Activityに到達する場合、正しい戻り値が評価されるようにFinish Activity名を指定することが必要な場合があります。
注:サブフローで使用されるアクティビティが遅延や待機を引き起こさないことが重要です。トークンが遅延や待機で中断された場合、executesubflow関数の終了時にトークンがFinish Activityに到達しません。
例
return executesubflow("SubFlow1", processor);
getactivity (node/obj/str token/processFlow [, str activityName])
getbatch (obj/str tokenOrBatch[, obj instanceObject, obj/str/num group])
説明
トークンまたは[グループ化の基準]値を使用して、バッチアクティビティ内のバッチを取得します。パラメータ1にトークンが渡された場合、instanceObjectおよびgroupパラメータは使用されません。
例
treenode batch = getbatch(token);
treenode batch = getbatch("Batch", current, 3);
treenode batch = getbatch("Batch", current, 3);
getchildtoken (node parentToken [, int childIndex])
getchildtokenrank (node childToken)
getlastacquiredresource (node resource, node token)
説明
resourceからtokenにより取得された最後のオブジェクトを取得します。
例
treenode operator = getlastacquiredresource(operatorResource, token);
getparenttoken (node token)
getprocessflowvar (obj/str processFlow, str varname[, node token])
説明
処理フロー変数の値を取得します。processflowパラメータは、ツール内の処理フローオブジェクトへの参照、または処理フローオブジェクトの名前です。
例
double processTime = getprocessflowvar(processflow, "processTime"); treenode processor = getprocessflowvar(processflow, "processor", token);
gettoken (obj instanceObject, obj/str activity, num index)
説明
与えられた所有者オブジェクト(インスタンス)用のアクティビティのインデックスにあるトークンを取得します。
例
treenode token = gettoken(fixedResource, activity, 3);
treenode token = gettoken(processor3, "Wait for Conveyor", 2);
treenode token = gettoken(processor3, "Wait for Conveyor", 2);
gettokenbyid (num id [, obj/str processFlow])
gettokens (obj instanceObject, obj activityOrAsset[, num flags])
説明
アクティビティまたは共有アセットの「内部」にあるすべてのトークンを取得します。アクティビティの場合、そのアクティビティ内にあるトークンの現在のセットです。リソースの場合、そのリソースを取得したトークンのセットです。ゾーンの場合、そのゾーンに進入したトークンのセットです。リストの場合、そのリストにプッシュされたトークンのセットです。結果を含む配列を返します。
instanceObject - 目的の処理フローインスタンスと関連付けられているオブジェクト。一般的な処理フローの場合、処理フロー自身と同じです。タスク実行者および固定リソースの処理フローの場合、3Dオブジェクト、すなわち処理フローインスタンスと関連付けられているタスク実行者または固定リソースです。処理フローアクティビティのロジックから実行された場合、通常は単に「current」です。ここにNULLを渡すと、すべてのインスタンスのトークンが得られます。
activityOrAsset - 対象アクティビティまたは共有アセット。NULLの場合、このコマンドは処理フローインスタンス全体に含まれる、すべてのアクティブなトークンを返します。
flags - オプションフラグを定義します。共有アセットについてGET_TOKENS_REQUESTSが渡された場合、共有アセットを要求しているトークンのセットが返されます(ゾーン進入の待機中のトークン、リストでバックオーダーのトークンなど)。
instanceObject - 目的の処理フローインスタンスと関連付けられているオブジェクト。一般的な処理フローの場合、処理フロー自身と同じです。タスク実行者および固定リソースの処理フローの場合、3Dオブジェクト、すなわち処理フローインスタンスと関連付けられているタスク実行者または固定リソースです。処理フローアクティビティのロジックから実行された場合、通常は単に「current」です。ここにNULLを渡すと、すべてのインスタンスのトークンが得られます。
activityOrAsset - 対象アクティビティまたは共有アセット。NULLの場合、このコマンドは処理フローインスタンス全体に含まれる、すべてのアクティブなトークンを返します。
flags - オプションフラグを定義します。共有アセットについてGET_TOKENS_REQUESTSが渡された場合、共有アセットを要求しているトークンのセットが返されます(ゾーン進入の待機中のトークン、リストでバックオーダーのトークンなど)。
例
Array tokensInActivity = gettokens(current, getactivity(processFlow, "Wait For Exit")); Array resourceOwners = gettokens(current, getactivity(processFlow, "Resource1"));
releasebatch (node batch, int failed [, int/str/obj connector])
説明
バッチアクティビティからバッチをリリースします。failedが1の場合、バッチのすべてのトークンがリリースされ、リリース数量とラベル値は無視されます。
例
releasebatch(batch, false);
releasebatch(batch, true, "Failed");
releasebatch(batch, true, getactivity(processFlow, "Garbage"));
releasebatch(batch, true, "Failed");
releasebatch(batch, true, getactivity(processFlow, "Garbage"));
releasetoken (node token [, int/str/obj connectorOrActivity])
releasewave (node wave)
説明
同期または結合アクティビティからwaveをリリースします。
例
releasewave(wave);
settokencolor (node token, num red{0-255}, num green{0-255}, num blue{0-255} [, num alpha{0-255}])
settokenshape (node token, num index)
zonecheckrequests (obj instanceObject, obj/str zone)
説明
ゾーンのリクエストリストに存在するすべてのトークンを再評価します。
例
zonecheckrequests(fixedResource, "Zone 1")
zonegetpartitionvaluefortoken (obj zone, obj token)
説明
与えられたゾーンのトークンのパーティション値を取得します。
例
zonegetpartitionvaluefortoken(zone, token)
zoneistokeninsubset (obj zone, obj token, str subsetName)
説明
与えられたトークンが、与えられたゾーンの名前付きサブセットに存在するかどうかを判定します。
例
zoneistokeninsubset(zone, token, "MySubset")
ラックオブジェクト
ラックオブジェクトへのアクセスとデータの割り当てを行うコマンド。
rackdrawfilledcell (obj rack, num bay, num level, num x, num y, num z, num sx, num sy, num sz, num red, num green, num blue)
rackの与えられたbayとlevelにボックスを描画する
説明
rackの与えられたbayとlevelにボックスを描画します。x、y、zは0~1の数値で、ボックスの描画をセル内のどこから開始するかを割合で表します。sx、sy、szは0~1の数値で、ボックスのサイズを割合で表します。red、green、blueはボックスの色を指定します。
ボックスが正しく描画されることを保証するため、drawトリガーでこのコマンドを呼び出す前にfglDisable(GL_TEXTURE_2D)でOpenGLテクスチャを無効にします。
ボックスが正しく描画されることを保証するため、drawトリガーでこのコマンドを呼び出す前にfglDisable(GL_TEXTURE_2D)でOpenGLテクスチャを無効にします。
例
fglDisable(GL_TEXTURE_2D);
for (int bay = 1; bay <= 5; bay++) {
for (int level = 1; level <= 3; level++) {
rackdrawfilledcell(current, bay, level, 0,0,0, 0.5,1,1, 255,0,0);
}
}
fglEnable(GL_TEXTURE_2D);
この例は、bay 1~5、level 1~3に、各セルの容積の半分を占める(sx = 0.5, sy =1, sz = 1)赤色のボックスを描画します。
for (int bay = 1; bay <= 5; bay++) {
for (int level = 1; level <= 3; level++) {
rackdrawfilledcell(current, bay, level, 0,0,0, 0.5,1,1, 255,0,0);
}
}
fglEnable(GL_TEXTURE_2D);
この例は、bay 1~5、level 1~3に、各セルの容積の半分を占める(sx = 0.5, sy =1, sz = 1)赤色のボックスを描画します。
rackdrawvirtualcontent (obj rack, num bayfillperc, num levelfillperc, num itemdepth, num red, num green, num blue, num virtualonly)
rackの仮想コンテンツを描画する
説明
rackの「仮想」コンテンツを描画します。このコマンドは通常、rackrecycleitemコマンドを使用してフローアイテムをリサイクルするときのみ使用します。このコマンドが実行されるとき、rackはコンテンツテーブルを走査し、rackのすべてのフローアイテムについて、適切なベイおよびレベルにボックスを描画します。virtualonlyが1なら、スロットが埋まっているが、フローアイテムが存在しない(フローアイテムがリサイクルされた)スポットにのみボックスを描画します。bayfillpercとlevelfillpercは0~1の値で、描画されるボックスでセルのどれだけの割合を塗りつぶすかを指定します。Item depthは、ラックの内の各アイテムが占めるサイズです。床置きラックの場合、これはアイテムのzサイズです。通常のラックの場合はアイテムのyサイズです。
例
rackdrawvirtualcontent(current, 0.9,0.9,3, 256,0, 0, 1);
rackgetbaycontent (obj rack, num bay)
rackのbay内にあるフローアイテムの数を取得する
説明
rackの指定されたbayにあるフローアイテムの数を返します。
例
int numitems = rackgetbaycontent(current, 5);
numitemsを、currentラックのベイ5にあるフローアイテムの数に設定します。
numitemsを、currentラックのベイ5にあるフローアイテムの数に設定します。
rackgetbayloc (obj rack, num bay)
ベイのxの場所をラックの原点からの相対位置として取得する
説明
rackの指定されたbayのxの場所を、rackの原点からの相対位置として返します。
例
rackgetbayloc(current, 5);
ベイ5のrzを返します。
ベイ5のrzを返します。
rackgetbayofitem (obj rack, obj item)
アイテムが配置されているラックのベイ番号を取得する
説明
itemが配置されているrackのベイ番号を返します。
例
int baynum = rackgetbayofitem(current, item);
baynumを、currentラックでitemが含まれているベイ番号に設定します。
baynumを、currentラックでitemが含まれているベイ番号に設定します。
rackgetbaysize (obj rack, num bay)
ラックのベイのxサイズを取得する
説明
rackの指定されたbayのxサイズを返します。
例
rackgetbaysize(current, 5);
ベイ5のサイズを返します。
ベイ5のサイズを返します。
rackgetcellcontent (obj rack, num bay, num level)
ラックのベイおよびレベルにあるフローアイテムの数を取得する
説明
rackの指定されたbayおよびlevelにあるフローアイテムの数を返します。
例
int numitems = rackgetcellcontent(current, 5, 3);
numitemsを、currentラックのベイ5、レベル3にあるフローアイテムの数に設定します。
numitemsを、currentラックのベイ5、レベル3にあるフローアイテムの数に設定します。
rackgetcellvar (obj rack, num bay, num level, num varnum, node storagenode)
説明
3次元のテーブルに格納されている値を返します。このテーブルの行はラックのベイを表します。
列はラックのレベルを表し、
テーブルセルのサブノードは、ラックの各セルに別々に格納されている値を表します。
これにより、ラックの各セルにカスタム情報を格納できます。
bay、level、varnumは、テーブルのベイ(行)、レベル(列)、変数番号(サブノードのランク)を参照します。
storagenodeは、このテーブルを格納したノードを参照します。これは通常、ラック上のラベルです。
列はラックのレベルを表し、
テーブルセルのサブノードは、ラックの各セルに別々に格納されている値を表します。
これにより、ラックの各セルにカスタム情報を格納できます。
bay、level、varnumは、テーブルのベイ(行)、レベル(列)、変数番号(サブノードのランク)を参照します。
storagenodeは、このテーブルを格納したノードを参照します。これは通常、ラック上のラベルです。
例
int typeofcellitems = rackgetcellvar(current, 1,5,3, current.labels["storageData"]);
rackgetitembybaylevel (obj rack, num bay, num level, num itemrank)
ラックのベイおよびレベルにあるアイテムへの参照を取得する
説明
rackの指定されたbayおよびlevelにあるアイテムへの参照を返します。itemrankは、そのセルにあるアイテムのランクを指定します。
例
treenode theitem = rackgetitembybaylevel(current, 5, 4, 2);
theitemポインターを、currentオブジェクトのベイ5、レベル4にある2番目のフローアイテムに設定します。
theitemポインターを、currentオブジェクトのベイ5、レベル4にある2番目のフローアイテムに設定します。
rackgetitemcellrank (obj rack, obj item)
ラックのセル内にあるアイテムのランクを取得する
説明
rackの与えられたセル内にあるitemのランクを返します。
例
int theRank = rackgetitemcellrank(current, item);
rackgetlevelloc (obj rack, num bay, num level)
ラックの原点に相対的なレベルのyまたはzの場所を取得する
説明
rackの与えられたlevelのyまたはzの場所を、rackの原点に対する相対位置として返します。
rackが床置きラックなら、y rzが返されます。
rackが通常のラックなら、z rzが返されます。
rackが床置きラックなら、y rzが返されます。
rackが通常のラックなら、z rzが返されます。
例
rackgetlevelloc(current, 5, 4);
ベイ5、レベル4のyまたはzの場所を返します。
ベイ5、レベル4のyまたはzの場所を返します。
rackgetlevelofitem (obj rack, obj item)
アイテムが配置されているラックのレベル番号を取得する
説明
itemが配置されているrackのレベル番号を返します。
例
int levelnum = rackgetlevelofitem(current, item);
levelnum変数を、currentラックでitemが含まれているレベル番号に設定します。
levelnum変数を、currentラックでitemが含まれているレベル番号に設定します。
rackgetlevelsize (obj rack, num bay, num level)
ラックのレベルのyまたはzサイズを取得する
説明
rackの与えられたlevelのyまたはzサイズを返します。
rackが床置きラックなら、yサイズを返します。
rackが通常のラックなら、zサイズを返します。
rackが床置きラックなら、yサイズを返します。
rackが通常のラックなら、zサイズを返します。
例
rackgetlevelsize(current, 5, 4);
ベイ5、レベル4のyまたはzサイズを返します。
ベイ5、レベル4のyまたはzサイズを返します。
rackgetnrofbays (obj rack)
ラックに存在するベイの数を取得する
説明
rackに存在するベイの数を返します。
例
return duniform(1,rackgetnrofbays(rack));
1から、rackのベイ数までの間のランダムな数値を返します。これは、ベイのピックリストにある[ランダム]オプションと同じ動作です。
1から、rackのベイ数までの間のランダムな数値を返します。これは、ベイのピックリストにある[ランダム]オプションと同じ動作です。
rackgetnroflevels ( obj rack [,num bay ] )
ラックのベイ内にあるレベルの数を取得する
説明
rackの指定されたbay内のレベルの数を返します。関数にbayパラメータが渡されない場合、最初のベイのnroflevelsが返されます。
例
return duniform(1,rackgetnroflevels(rack, baynum));
1から、rackの選択したベイにあるレベル数までの間のランダムな数値を返します。これは、レベルのピックリストにある[ランダム]オプションと同じ動作です。
1から、rackの選択したベイにあるレベル数までの間のランダムな数値を返します。これは、レベルのピックリストにある[ランダム]オプションと同じ動作です。
rackrecycleitem (obj rack, obj item, num binrank)
フローアイテムをFlowItem Binにリサイクルする
説明
フローアイテムを指定されたFlowitem Binにリサイクルします。
このコマンドは高度なユーザー向けで、デバッグを行う用意がなければ使用すべきではありません。
binrankは、Flowitem Bin内でのフローアイテムのランクです(テクスチャありの色付きボックス = 5など)。
このコマンドが呼び出されるとき、フローアイテムはリサイクルされますが、フローアイテムが配置されていたスポットは使用中として割り当てられ、
以後のフローアイテムは、そのスポットが既に使用されている場合と同様にラックに置かれます。
これにより、モデルの速度が大幅に向上する可能性があります。
rackgetbaycontent()やrackgetcellcontent()などへの以後のコマンドは、アイテムが依然としてそこに存在するものとして値を返します。
ただし、rackgetitembybaylevel()は、リサイクルされ、復元されていないアイテムについてNULLを返します。
このコマンドを呼び出す前に、アイテムがリリース済みまたは輸送の待機中でないことを確認してください。
このコマンドが使用された場合、ラックの最大コンテンツは正しく動作しないことに注意してください。また、アイテムは後でrackrestoreitem()コマンドを使用して
復元する必要があります。
このコマンドは高度なユーザー向けで、デバッグを行う用意がなければ使用すべきではありません。
binrankは、Flowitem Bin内でのフローアイテムのランクです(テクスチャありの色付きボックス = 5など)。
このコマンドが呼び出されるとき、フローアイテムはリサイクルされますが、フローアイテムが配置されていたスポットは使用中として割り当てられ、
以後のフローアイテムは、そのスポットが既に使用されている場合と同様にラックに置かれます。
これにより、モデルの速度が大幅に向上する可能性があります。
rackgetbaycontent()やrackgetcellcontent()などへの以後のコマンドは、アイテムが依然としてそこに存在するものとして値を返します。
ただし、rackgetitembybaylevel()は、リサイクルされ、復元されていないアイテムについてNULLを返します。
このコマンドを呼び出す前に、アイテムがリリース済みまたは輸送の待機中でないことを確認してください。
このコマンドが使用された場合、ラックの最大コンテンツは正しく動作しないことに注意してください。また、アイテムは後でrackrestoreitem()コマンドを使用して
復元する必要があります。
例
rackrecycleitem(current, item, 5);
フローアイテムを、Flowitem Binのランク5のフローアイテム(通常はテクスチャありの色付きボックス)にリサイクルします。
フローアイテムを、Flowitem Binのランク5のフローアイテム(通常はテクスチャありの色付きボックス)にリサイクルします。
rackrestoreitem (obj rack, num binrank, num bay, num level, num position)
フローアイテムをFlowitem Binからベイとレベルに復元する
説明
フローアイテムをFlowitem Binから、与えられたbayとlevelに復元します。
例
rackrestoreitem(current, 5, 7, 3, 1);
フローアイテムをFlowitem Binのランク5のフローアイテム(通常はテクスチャありの色付きボックス)から、ラックのベイ7、レベル3、位置1に復元します。
フローアイテムをFlowitem Binのランク5のフローアイテム(通常はテクスチャありの色付きボックス)から、ラックのベイ7、レベル3、位置1に復元します。
racksetcellcontent (obj rack, num bay, num level, num contentval)
ラックのセルの仮想コンテンツをcontentvalに設定する
説明
rackのセルの「仮想」コンテンツを指定された値に設定します。
このコマンドは、rackrecycleitem()とrackrestoreitem()を使用して、ラックとの間でアイテムのリサイクルと復元を行うときのみ使用します。
このコマンドは通常、リセット時に初期値の「仮想」コンテンツを設定するため使用されます。
このコマンドは、rackrecycleitem()とrackrestoreitem()を使用して、ラックとの間でアイテムのリサイクルと復元を行うときのみ使用します。
このコマンドは通常、リセット時に初期値の「仮想」コンテンツを設定するため使用されます。
例
racksetcellcontent(current, 5, 3, 2);
racksetcellvar (obj rack,num bay, num level, num varnum, num setvalue, node storagenode)
説明
3次元のテーブルに値を設定します。このテーブルの行はラックのベイを表します。
列はラックのレベルを表し、
テーブルセルのサブノードは、ラックの各セルに別々に格納されている値を表します。
これにより、ラックの各セルにカスタム情報を格納できます。
bay、level、varnumは、テーブルのベイ(行)、レベル(列)、変数番号(サブノードのランク)を参照します。
setvalueは設定する値です。
storagenodeは、このテーブルが格納されているノードを参照します。これは通常、ラック上のラベルです。
列はラックのレベルを表し、
テーブルセルのサブノードは、ラックの各セルに別々に格納されている値を表します。
これにより、ラックの各セルにカスタム情報を格納できます。
bay、level、varnumは、テーブルのベイ(行)、レベル(列)、変数番号(サブノードのランク)を参照します。
setvalueは設定する値です。
storagenodeは、このテーブルが格納されているノードを参照します。これは通常、ラック上のラベルです。
例
racksetcellvar(current, 5, 3, 2, 4.6, current.labels["storageData"]);
ベイ5、レベル3の2番目の値を4.6に設定します。
ベイ5、レベル3の2番目の値を4.6に設定します。
統計
統計データの作成、操作、アクセスを行うコマンドで、確率分布も含まれます。
addbundleentry (node datanode[, field1val, field2val, ...])
バンドルに新しいエントリを追加する(0から開始)
説明
バンドルに新しいエントリを追加します(0から開始)。エントリを追加する前に、すべてのフィールドを追加する必要があります。オプションフィールドの値は、指定された順序でフィールドに追加されます。最大で29のフィールドの値を指定できます。これよりフィールドの多いバンドルについては、setbundlevalueを使用してください。
例
int lastentry = addbundleentry(x, time(), current.subnodes.length);
addbundlefield (node datanode, str fieldname, num type[, num maxstrsize])
バンドルにフィールドを追加する
説明
バンドルにフィールドを、与えられたフィールド名で追加します。追加されたフィールドのフィールドランク(0から開始)を返します。エントリを追加する前に、バンドルのすべてのフィールドを追加する必要があります。typeはビット単位のフラグで、次のいずれかの値です。
BUNDLE_FIELD_TYPE_DOUBLE:64ビットのdoubleを格納します。
BUNDLE_FIELD_TYPE_FLOAT:32ビットのfloatを格納します。
BUNDLE_FIELD_TYPE_INT:32ビットのintegerを格納します。
BUNDLE_FIELD_TYPE_STR:文字列を格納します。使用する場合、文字列の最大サイズも定義します。これは各文字列エントリに割り当てられる容量です。maxstrsizeが指定されない場合、デフォルトは32バイトです。このフィールドは、最低でも指定された長さの文字列を格納でき、それより長い文字列は切り捨てられます。
BUNDLE_FIELD_TYPE_VARCHAR:文字列を格納します。このフィールドタイプでは、文字列の長さの制限はありません。文字列の長さが可変の場合、または文字列が頻繁に繰り返される場合、このフィールドタイプをお勧めします。
BUNDLE_FIELD_TYPE_NODEREF:ノードへの参照を格納します。
BUNDLE_FIELD_TYPE_BINARY:1または0を単一のビットとして格納します。ビットは32のブロック単位で割り当てられるため、1つのバイナリフィールドには32ビットが必要です。ただし、32のバイナリフィールドは1つのブロックを共有できます。
オプションとして、上記の値のどれでも(BUNDLE_FIELD_TYPE_BINARYを除く)BUNDLE_FIELD_INDEX_MAPとビット単位で組み合わせることができます。このタイプのフィールドに含まれるすべての値は、getbundleindexentries()を使用して迅速にルックアップ(O(log n))できるようインデックス付けされます。
オプションとして、BUNDLE_FIELD_TYPE_INT、BUNDLE_FIELD_TYPE_STR、BUNDLE_FIELD_TYPE_VARCHAR、またはBUNDLE_FIELD_TYPE_NODEREFをBUNDLE_FIELD_INDEX_HASHと組み合わせることができます。このタイプのフィールドに含まれるすべての値は、getbundleindexentries()を使用して迅速にルックアップ(O(1))できるようインデックス付けされます。このタイプのフィールドは、モデルの実行中にバンドルのサイズが変更することがほとんど、またはまったくない場合のみ使用することをお勧めします。
オプションとして、上記のどの値でも(BUNDLE_FIELD_TYPE_BINARYを除く)BUNDLE_FIELD_NULLABLEと組み合わせることができ、それによってフィールドにnull値を格納可能になります。フィールドにnull値が許可される場合、setbundlevalue()にnullバリアントを渡すことができ、getbundlevalue()からもnullバリアントが得られることがあります。
BUNDLE_FIELD_TYPE_DOUBLE:64ビットのdoubleを格納します。
BUNDLE_FIELD_TYPE_FLOAT:32ビットのfloatを格納します。
BUNDLE_FIELD_TYPE_INT:32ビットのintegerを格納します。
BUNDLE_FIELD_TYPE_STR:文字列を格納します。使用する場合、文字列の最大サイズも定義します。これは各文字列エントリに割り当てられる容量です。maxstrsizeが指定されない場合、デフォルトは32バイトです。このフィールドは、最低でも指定された長さの文字列を格納でき、それより長い文字列は切り捨てられます。
BUNDLE_FIELD_TYPE_VARCHAR:文字列を格納します。このフィールドタイプでは、文字列の長さの制限はありません。文字列の長さが可変の場合、または文字列が頻繁に繰り返される場合、このフィールドタイプをお勧めします。
BUNDLE_FIELD_TYPE_NODEREF:ノードへの参照を格納します。
BUNDLE_FIELD_TYPE_BINARY:1または0を単一のビットとして格納します。ビットは32のブロック単位で割り当てられるため、1つのバイナリフィールドには32ビットが必要です。ただし、32のバイナリフィールドは1つのブロックを共有できます。
オプションとして、上記の値のどれでも(BUNDLE_FIELD_TYPE_BINARYを除く)BUNDLE_FIELD_INDEX_MAPとビット単位で組み合わせることができます。このタイプのフィールドに含まれるすべての値は、getbundleindexentries()を使用して迅速にルックアップ(O(log n))できるようインデックス付けされます。
オプションとして、BUNDLE_FIELD_TYPE_INT、BUNDLE_FIELD_TYPE_STR、BUNDLE_FIELD_TYPE_VARCHAR、またはBUNDLE_FIELD_TYPE_NODEREFをBUNDLE_FIELD_INDEX_HASHと組み合わせることができます。このタイプのフィールドに含まれるすべての値は、getbundleindexentries()を使用して迅速にルックアップ(O(1))できるようインデックス付けされます。このタイプのフィールドは、モデルの実行中にバンドルのサイズが変更することがほとんど、またはまったくない場合のみ使用することをお勧めします。
オプションとして、上記のどの値でも(BUNDLE_FIELD_TYPE_BINARYを除く)BUNDLE_FIELD_NULLABLEと組み合わせることができ、それによってフィールドにnull値を格納可能になります。フィールドにnull値が許可される場合、setbundlevalue()にnullバリアントを渡すことができ、getbundlevalue()からもnullバリアントが得られることがあります。
例
addbundlefield(x, "Object Name", BUNDLE_FIELD_TYPE_STR | BUNDLE_FIELD_NULLABLE, 64);
bernoulli (num prob, num succeed-value, num fail-value[, num stream])
与えられた確率に基づいて、2つの可能な値のいずれかを返す
説明
bernoulli( p, a, b, stream )は離散確率分布です。
入力:
pは、aが返される確率です。ここでp∈ ( 0, 100 )
100 −pは、bが返される確率です。
a∈ ( - ∞, ∞ )
b∈ ( - ∞, ∞ )
streamは、FlexSimの乱数ストリーム{0,1,2,...}の1つへの参照です。
出力:
範囲 = { a , b }
平均値 = ( ap + b(100−p) ) ⁄ 100
分散 = (p⁄100)(1 −p⁄100) a=1かつb=0の場合
可能な用途:
合格/失格テストなど、2つの結果が存在し得るランダムな状況をモデル化するため使用されます。bernoulliコマンドをネストして、2つより多くの値を生成できますが、その場合は経験的分布を使用する方が適切です。
コメント:
bernoulli(p, 1, 0)とbinomial(1, p)の分布は同一です。
入力:
pは、aが返される確率です。ここでp∈ ( 0, 100 )
100 −pは、bが返される確率です。
a∈ ( - ∞, ∞ )
b∈ ( - ∞, ∞ )
streamは、FlexSimの乱数ストリーム{0,1,2,...}の1つへの参照です。
出力:
範囲 = { a , b }
平均値 = ( ap + b(100−p) ) ⁄ 100
分散 = (p⁄100)(1 −p⁄100) a=1かつb=0の場合
可能な用途:
合格/失格テストなど、2つの結果が存在し得るランダムな状況をモデル化するため使用されます。bernoulliコマンドをネストして、2つより多くの値を生成できますが、その場合は経験的分布を使用する方が適切です。
コメント:
bernoulli(p, 1, 0)とbinomial(1, p)の分布は同一です。
例
treenode curoperator = current.centerObjects[bernoulli(90,1,2,1)];
この例のbernoulliコマンドは、乱数ストリーム1を使用して90%の確率で1を、それ以外は2を返します。centerObject参照の中で使用され、curoperatorは90%の確率でcurrentオブジェクトのセンターポート1に接続されたオブジェクトを、残りの確率でセンターポート2に接続されたオブジェクトを参照します。
この例のbernoulliコマンドは、乱数ストリーム1を使用して90%の確率で1を、それ以外は2を返します。centerObject参照の中で使用され、curoperatorは90%の確率でcurrentオブジェクトのセンターポート1に接続されたオブジェクトを、残りの確率でセンターポート2に接続されたオブジェクトを参照します。
beta (num min, num max, num shape1, num shape2[, num stream])
ベータ分布からランダムなサンプルを返す
説明
beta( a, b, α1, α2, stream )は有界の連続した確率分布です。
入力:
aは下限パラメータ ∈ ( - ∞, ∞ )
bは上限パラメータ( b > a )
α1は1番目の形状パラメータ( 0, ∞ )
α2は2番目の形状パラメータ( 0, ∞ )
streamはFlexSimの乱数ストリーム{0,1,2,...}の1つへの参照
出力:
範囲 = ( a , b )
平均値 = a + α1(b−a) ⁄ (α1 + α2)
分散 = α1α2(b−a)²⁄ (α1 + α2)²(α1 + α2 + 1)
確率密度関数:
可能な用途:
ベータ分布は多くの場合、実際のデータが存在しない場合にタスクの期間をモデル化するため使用されます。この分布は必ず最小値と最大値の間に収まり、使用される2つの形状パラメータによって多くの異なる確率密度形状が得られるためです。ほとんどの現実世界でのタスク期間について、密度の形状は左側よりも右側のテールが長くなるため、平均値μと最頻値(ほとんどの場合は値)mが判明していれば、次の式を使用して適切な形状パラメータを逆計算できます。
α1 ≅ ( μ−a)(2m−a−b) ⁄ (m−μ)(b−a)
α2 ≅ α1(b−μ) ⁄ (μ−a)
コメント:
beta( a, b, 1, 1)とuniform( a, b)の分布は同一です。
密度は(a + b) ⁄ 2に対して対称です(α1 = α2のとき)。
α2 > α1 > 1のときは、密度に突出部があり、右側のテールが長くなります。
α1 = α2 > 1のとき、平均値と最頻値は等しくなります。
入力:
aは下限パラメータ ∈ ( - ∞, ∞ )
bは上限パラメータ( b > a )
α1は1番目の形状パラメータ( 0, ∞ )
α2は2番目の形状パラメータ( 0, ∞ )
streamはFlexSimの乱数ストリーム{0,1,2,...}の1つへの参照
出力:
範囲 = ( a , b )
平均値 = a + α1(b−a) ⁄ (α1 + α2)
分散 = α1α2(b−a)²⁄ (α1 + α2)²(α1 + α2 + 1)
確率密度関数:

可能な用途:
ベータ分布は多くの場合、実際のデータが存在しない場合にタスクの期間をモデル化するため使用されます。この分布は必ず最小値と最大値の間に収まり、使用される2つの形状パラメータによって多くの異なる確率密度形状が得られるためです。ほとんどの現実世界でのタスク期間について、密度の形状は左側よりも右側のテールが長くなるため、平均値μと最頻値(ほとんどの場合は値)mが判明していれば、次の式を使用して適切な形状パラメータを逆計算できます。
α1 ≅ ( μ−a)(2m−a−b) ⁄ (m−μ)(b−a)
α2 ≅ α1(b−μ) ⁄ (μ−a)
コメント:
beta( a, b, 1, 1)とuniform( a, b)の分布は同一です。
密度は(a + b) ⁄ 2に対して対称です(α1 = α2のとき)。
α2 > α1 > 1のときは、密度に突出部があり、右側のテールが長くなります。
α1 = α2 > 1のとき、平均値と最頻値は等しくなります。
例
double ptime = beta(8, 12, 1.3, 3, 5);
変数ptime variableはベータ分布と等しい値に設定され、最小値は8、最大値は12で、α1とα2にはそれぞれ形状係数1.3と3が使用されます。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。分布密度には突出部の曲線があり、右側のテールが長くなります。
変数ptime variableはベータ分布と等しい値に設定され、最小値は8、最大値は12で、α1とα2にはそれぞれ形状係数1.3と3が使用されます。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。分布密度には突出部の曲線があり、右側のテールが長くなります。
binomial (num trials, num prob[, num stream])
二項分布からランダムなサンプルを返す
説明
binomial( t, p, stream )は離散確率分布で、t回の独立したベルヌーイ試行を、試行ごとの成功確率pで行った場合の成功回数を表すために使用されます。
入力:
tは独立した試行の回数{ 1, 2, ..., ∞ }
pは各試行の成功確率(0, 100)
streamは、FlexSimの乱数ストリームの1つへの参照{0,1,2,...}
出力:
範囲 = { 0, 1, 2, ..., t }
平均値 = tp⁄ 100
分散 = t ( p⁄ 100 )( 1 −p⁄ 100 )
可能な用途:
二項分布は、サイズtのバッチに含まれる不良部品の数、ランダムなサイズのグループに含まれる実際の人数、在庫から発注されたアイテムの数などをモデル化するために便利です。
コメント:
binomial(1, p )とbernoulli( p, 1, 0 )分布は同一です。
binomial( t, p )分布は、p = 50%のとき対称形になります。
入力:
tは独立した試行の回数{ 1, 2, ..., ∞ }
pは各試行の成功確率(0, 100)
streamは、FlexSimの乱数ストリームの1つへの参照{0,1,2,...}
出力:
範囲 = { 0, 1, 2, ..., t }
平均値 = tp⁄ 100
分散 = t ( p⁄ 100 )( 1 −p⁄ 100 )
可能な用途:
二項分布は、サイズtのバッチに含まれる不良部品の数、ランダムなサイズのグループに含まれる実際の人数、在庫から発注されたアイテムの数などをモデル化するために便利です。
コメント:
binomial(1, p )とbernoulli( p, 1, 0 )分布は同一です。
binomial( t, p )分布は、p = 50%のとき対称形になります。
例
int fparts = binomial(item.batchsize, 10, 5);
「batchsize」という名前のフローアイテムのラベルに定義されているバッチ数量内の部品の不良率が10%として、不良部品の数が変数fpartsに書き込まれます。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。
「batchsize」という名前のフローアイテムのラベルに定義されているバッチ数量内の部品の不良率が10%として、不良部品の数が変数fpartsに書き込まれます。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。
calculateconfidence (num stddev, num nrofdatapoints, num confidence)
説明
開発者向けです。与えられたデータポイントの標準偏差と数について、信頼区間を計算します。戻り値は、サンプルの平均値から、区間の片端までの距離です。信頼区間の計算にt分布を使用します。信頼度の値は90、95、99のいずれかです。実験ツールで、各シナリオのパフォーマンス指標の平均値について信頼区間を計算するために使用されます。
例
calculateconfidence(5.82, nrofsamples, 90)
cauchy (num location, num scale[, num stream])
コーシー分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、コーシー分布から連続的なランダム変量を生成します。
例
cempirical (str/node/num table[, num stream])
連続的な経験的分布からランダムなサンプルを返す
説明
連続的な経験的分布で、割合と値は指定の表で定義されます。
経験的分布は、ユーザーにより作成されたテーブルを参照し、このテーブルには値のリストと、それぞれの値に関連付けられた確率の割合が含まれています。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは、テーブルで定義された経験的分布からランダムな変量を生成するため、dempirical()、empirical()、cempirical()の3つのコマンドを使用できます。最初のコマンドは離散分布で、テーブルにリストされている明示的な値を返します。次の2つは有界の連続分布で、ある範囲内の連続した数値を返します。連続分布の場合、表の隣接する2つの値の間で値の補間が行われるため、列2の値は昇順にする必要があります。
テーブルに4つの行と2つの列があると想定します。列1は割合を表し、10、20、30、40で、合計は100%です。列2は値0.1、0.2、0.3、0.4です。離散的な経験的分布のコマンドと、2つの連続的な経験的分布のコマンドの違いについて考えてみます。離散的なコマンドでは、テーブルの列2に入力された値と正確に一致するランダムな変量のみが生成されます。連続的なコマンドでは、テーブルの列2で2つの隣接する数値の間で均等に分布する実数が、ランダムな変量として生成されます。2つの連続的なコマンドの間の相違は、均等な範囲の境界がどのように定義されるかです。
コマンドdempirical("mytable")は、サンプルのセットが非常に大きいと仮定して、サンプルの10%について数値0.1を、20%について0.2を、30%について0.3を、40%について0.4を返します。
コマンドempirical("mytable")は、サンプルの10%について0.1と0.2の間、20%について0.2と0.3の間、30%について0.3と0.4の間、40%について0.4と0.4の間で、それぞれ均等に分布する数値を返します。最後の40%を0.4ではなく、0.4と0.5の間の値にするには、5番目の行を追加し、列1に値0、列2に0.5(または希望する上限)を指定します。
コマンドcempirical("mytable")は、サンプルの10%について0.0と0.1の間、20%について0.1と0.2の間、30%について0.2と0.3の間、40%について0.3と0.4の間で、それぞれ均等に分布する数値を返します。最初の10%について0.0以外の下限を定義するには、行の先頭に行(行1)を追加し、列1に値0、列2に0.05(または希望する下限)を指定します。
3つの分布関数のそれぞれについて、可能な戻り値(「x」)の要約を表形式で次に示します。

「ダミーの」最初の行を追加し、cempirical()が0.0の代わりに0.05から始まるようにする例を次に示します(行1の割合は0%であることに注意してください)。
「ダミーの」最後の行を追加し、empirical()が最後の値を含むそれぞれの値の間の範囲を使用するようにする例を次に示します(最後の行の割合はどのような数値でもかまいません。前の行までで既に割合の合計が100%に達しているので、この割合は無視されます)。
ExpertFitを使用してデータに一致する経験的分布を判定するときは、データが整数として定義されているならExpertFitはdempirical()で使用するようデータを適合させ、データが実数として定義されているならempirical()で使用するようデータを適合させることに注意してください。データセットが実数で構成される場合、ExpertFitは最後の値について、最後の1つ前の値と同じ割合を表示しますが、最後の1つ前のエントリで確率の合計が100%に達していることが分かります。
経験的分布は、ユーザーにより作成されたテーブルを参照し、このテーブルには値のリストと、それぞれの値に関連付けられた確率の割合が含まれています。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは、テーブルで定義された経験的分布からランダムな変量を生成するため、dempirical()、empirical()、cempirical()の3つのコマンドを使用できます。最初のコマンドは離散分布で、テーブルにリストされている明示的な値を返します。次の2つは有界の連続分布で、ある範囲内の連続した数値を返します。連続分布の場合、表の隣接する2つの値の間で値の補間が行われるため、列2の値は昇順にする必要があります。
テーブルに4つの行と2つの列があると想定します。列1は割合を表し、10、20、30、40で、合計は100%です。列2は値0.1、0.2、0.3、0.4です。離散的な経験的分布のコマンドと、2つの連続的な経験的分布のコマンドの違いについて考えてみます。離散的なコマンドでは、テーブルの列2に入力された値と正確に一致するランダムな変量のみが生成されます。連続的なコマンドでは、テーブルの列2で2つの隣接する数値の間で均等に分布する実数が、ランダムな変量として生成されます。2つの連続的なコマンドの間の相違は、均等な範囲の境界がどのように定義されるかです。
コマンドdempirical("mytable")は、サンプルのセットが非常に大きいと仮定して、サンプルの10%について数値0.1を、20%について0.2を、30%について0.3を、40%について0.4を返します。
コマンドempirical("mytable")は、サンプルの10%について0.1と0.2の間、20%について0.2と0.3の間、30%について0.3と0.4の間、40%について0.4と0.4の間で、それぞれ均等に分布する数値を返します。最後の40%を0.4ではなく、0.4と0.5の間の値にするには、5番目の行を追加し、列1に値0、列2に0.5(または希望する上限)を指定します。
コマンドcempirical("mytable")は、サンプルの10%について0.0と0.1の間、20%について0.1と0.2の間、30%について0.2と0.3の間、40%について0.3と0.4の間で、それぞれ均等に分布する数値を返します。最初の10%について0.0以外の下限を定義するには、行の先頭に行(行1)を追加し、列1に値0、列2に0.05(または希望する下限)を指定します。
3つの分布関数のそれぞれについて、可能な戻り値(「x」)の要約を表形式で次に示します。

「ダミーの」最初の行を追加し、cempirical()が0.0の代わりに0.05から始まるようにする例を次に示します(行1の割合は0%であることに注意してください)。

「ダミーの」最後の行を追加し、empirical()が最後の値を含むそれぞれの値の間の範囲を使用するようにする例を次に示します(最後の行の割合はどのような数値でもかまいません。前の行までで既に割合の合計が100%に達しているので、この割合は無視されます)。

ExpertFitを使用してデータに一致する経験的分布を判定するときは、データが整数として定義されているならExpertFitはdempirical()で使用するようデータを適合させ、データが実数として定義されているならempirical()で使用するようデータを適合させることに注意してください。データセットが実数で構成される場合、ExpertFitは最後の値について、最後の1つ前の値と同じ割合を表示しますが、最後の1つ前のエントリで確率の合計が100%に達していることが分かります。
例
cempirical("mytable", 5);
「mytable」という名前のグローバルテーブルで定義されている連続的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
cempirical(current.labels["ptime"] 5);
currentオブジェクトの「ptime」という名前のラベルで定義されるノードテーブルで定義されている、連続的な経験的分布から、乱数ストリーム5を使用してランダムな変量を返します。
「mytable」という名前のグローバルテーブルで定義されている連続的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
cempirical(current.labels["ptime"] 5);
currentオブジェクトの「ptime」という名前のラベルで定義されるノードテーブルで定義されている、連続的な経験的分布から、乱数ストリーム5を使用してランダムな変量を返します。
clearbundle (node datanode[, num resetflags = 0])
すべてのバンドルデータをクリアする
説明
datanodeに関連付けられているバンドルデータをクリアします。これにより、バンドルのすべてのエントリと、すべてのフィールドがクリアされます。resetflagsは、バンドルの初期化に使用されるflagsのビット単位マスクです。有効な値は次のとおりです。
BUNDLE_FLAG_UNPAGED = 0x1 - バンドルのエントリは、ページなしの連続的なメモリブロックに格納されます。
BUNDLE_FLAG_IR_OPT = 0x10 - バンドルの中間に行を挿入/削除するときのパフォーマンス向上のため、追加メモリ(行ごとに32ビット)が使用されます。
BUNDLE_FLAG_UNPAGED = 0x1 - バンドルのエントリは、ページなしの連続的なメモリブロックに格納されます。
BUNDLE_FLAG_IR_OPT = 0x10 - バンドルの中間に行を挿入/削除するときのパフォーマンス向上のため、追加メモリ(行ごとに32ビット)が使用されます。
例
clearbundle(x);
dataplot (obj tree, num type, num action, num x, num y, num z)
説明
開発者向けです。このコマンドを使用して、ヒストグラム、x/yチャート、または連続したデータの作成、リセット、データの追加を行えます。最初の3つのパラメータは、ツリー内の関連するノードや、行うべき動作を定義します。最後の3つのパラメータx、y、zは、動作に使用される適切なデータを定義します。最初のパラメータは、グラフやヒストグラムのデータを保持するツリーのメインノードです。2番目のパラメータは1、2、3のいずれかで、ノードの保持するデータタイプを定義します。1はgraphxデータを意味します。このデータタイプでは、ノードにサブノードのリストが含まれ、各サブノードには連続したデータの固有のポイントである数値が含まれます。2はgraphxyを意味します。このデータタイプでも、ノードには同様にサブノードのリストが含まれますが、サブノードはx/yペアとして組み合わせられます。ランク1および2のノードには1つのデータポイントのxとyの値が保持され、3と4には次のデータポイントのxとyの値が保持され、以下同様にデータが保持されます。typeパラメータが3なら、ヒストグラムデータを意味します。ここでは、ノードにはヒストグラムに関連付けられているデータが保持されます。actionパラメータは1、2、3のいずれかで、行うべきアクションを定義します。1は作成操作です。この操作は、ノードのサブツリー構造のセッアップが必要な、ヒストグラムタイプのデータでのみ必要となります。ヒストグラムプロットを作成するには、ヒストグラムの最小値をx、最大値をy、分割数(バケット数)をzのパラメータとして渡します。actionパラメータの値が2なら、データのリセットを行います。これにより、graphxまたはgraphxyデータではノードのコンテンツがクリアされ、ヒストグラムデータではヒストグラムの値がリセットされます。actionパラメータの値が3なら、データポイントを追加します。graphxおよびヒストグラムデータでは、データポイントをxパラメータとして渡します。graphxyデータでは、xおよびyパラメータとして渡します。要約すると次のようになります。タイプ:1-graphx/2-graphxy/3-ヒストグラム
アクション:1-作成(ヒストグラムデータでのみ必要)/2-リセット/3-ポイントの追加
データ:xとyはデータポイント(ヒストグラム作成の場合、x=開始、y=終了、z=分割数)
アクション:1-作成(ヒストグラムデータでのみ必要)/2-リセット/3-ポイントの追加
データ:xとyはデータポイント(ヒストグラム作成の場合、x=開始、y=終了、z=分割数)
例
dataplot(stats_contentgraph(model.find("Processor2")),2,3,8.6,5,0); Processor2のコンテンツグラフに、timeが8.6、contentが5のポイントを追加します。この例は、使用法を紹介するためだけのものです。Processorはコンテンツグラフを自動的に保守するため、実際にこのコマンドを使用する必要はありません。
dempirical (str/node/num table[, num stream])
離散的な経験的分布からランダムなサンプルを返す
説明
離散的な経験的分布。
参照されるテーブルには、値と、それぞれの値に関連付けられている確率の割合のリストが含まれている必要があります。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは3つの経験的分布が使用されます。それらの相違点と詳細については、cempirical()コマンドの説明を参照してください。
参照されるテーブルには、値と、それぞれの値に関連付けられている確率の割合のリストが含まれている必要があります。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは3つの経験的分布が使用されます。それらの相違点と詳細については、cempirical()コマンドの説明を参照してください。
例
int ptype = dempirical("prodtypes", 5);
「prodtypes」という名前のグローバルテーブルで定義されている離散的な経験的分布を使用し、乱数ストリーム5を使って、変数ptypeに値を割り当てます。
dempirical(current.labels["route"], 5);
currentオブジェクトの「route」という名前のラベルに定義されているノードテーブルで定義される離散的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
「prodtypes」という名前のグローバルテーブルで定義されている離散的な経験的分布を使用し、乱数ストリーム5を使って、変数ptypeに値を割り当てます。
dempirical(current.labels["route"], 5);
currentオブジェクトの「route」という名前のラベルに定義されているノードテーブルで定義される離散的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
duniform (num min, num max[, num stream])
minとmaxの間のランダムな整数を返す
説明
duniform( a, b, stream ) は有界な離散的確率分布です。
入力:
aは下限を指定するパラメータです。
bは上限を指定するパラメータです。
aとbは整数で、a < bです。
b−aはスケーリングのパラメータとなります。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = { a, a+1, ..., b }
平均値 = ( a + b ) ⁄ 2
分散 = ( (b−a + 1)²− 1 ) ⁄ 12
可能な用途:
aとbとの間でランダムに分布し、他の特性がほぼ未知の数量を概算するため使用されます。
コメント:
a、b、またはその間に存在する任意の離散的な(整数の)数値が等しい確率で返されます。
入力:
aは下限を指定するパラメータです。
bは上限を指定するパラメータです。
aとbは整数で、a < bです。
b−aはスケーリングのパラメータとなります。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = { a, a+1, ..., b }
平均値 = ( a + b ) ⁄ 2
分散 = ( (b−a + 1)²− 1 ) ⁄ 12
可能な用途:
aとbとの間でランダムに分布し、他の特性がほぼ未知の数量を概算するため使用されます。
コメント:
a、b、またはその間に存在する任意の離散的な(整数の)数値が等しい確率で返されます。
例
duniform(1, 6, 3);
最小値が1、最大値が6の離散的な一様分布から、乱数ストリーム3を使用してランダムな変量を生成します。これは、サイコロを振った結果をシミュレートします。
最小値が1、最大値が6の離散的な一様分布から、乱数ストリーム3を使用してランダムな変量を生成します。これは、サイコロを振った結果をシミュレートします。
empirical (str/node/num table[, num stream])
説明
連続的な経験的分布。
参照されるテーブルには、値と、それぞれの値に関連付けられている確率の割合のリストが含まれている必要があります。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは3つの経験的分布が使用されます。それらの相違点と詳細については、cempirical()コマンドの説明を参照してください。
参照されるテーブルには、値と、それぞれの値に関連付けられている確率の割合のリストが含まれている必要があります。確率の割合はテーブルの行1から開始される列1に、関連付けられている値は列2に入力する必要があります。テーブルには必要なだけ多くの値を定義でき、行数に制限はありません。割合には0~100の数値を入力し、合計は100%になるようにします。100%にならない場合、累積の割合が100を超えた後に定義される数値は決して返されません。
FlexSimでは3つの経験的分布が使用されます。それらの相違点と詳細については、cempirical()コマンドの説明を参照してください。
例
empirical("mytable", 5);
「mytable」という名前のグローバルテーブルで定義されている連続的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
empirical(current.labels["ptime"], 5);
currentオブジェクトの「ptime」という名前のラベルで定義されるテーブルで定義されている、連続的な経験的分布から、乱数ストリーム5を使用してランダムな変量を返します。
「mytable」という名前のグローバルテーブルで定義されている連続的な経験的分布から、乱数ストリーム5を使用して、ランダムな変量を返します。
empirical(current.labels["ptime"], 5);
currentオブジェクトの「ptime」という名前のラベルで定義されるテーブルで定義されている、連続的な経験的分布から、乱数ストリーム5を使用してランダムな変量を返します。
erlang (num location, num scale, num shape[, num stream])
アーラン分布からランダムなサンプルを返す
説明
erlang( γ, β, m, stream )は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケーリングパラメータです( β > 0 )。
mは形状パラメータです ∈ {1, 2, ...}。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + mβ
分散 = mβ²
可能な用途:
組み立て、顧客サービス、機械の修理などのタスクが完了するまでの時間をモデル化するために使用されます。
コメント:
γ = 0のとき、この分布はm-Erlang(β)分布と呼ばれます。
exponential( γ, β )とerlang( γ, β, 1 )分布は同一です。
正の整数mについて、gamma( γ, β, m )とerlang( γ, β, m )分布は同一です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケーリングパラメータです( β > 0 )。
mは形状パラメータです ∈ {1, 2, ...}。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + mβ
分散 = mβ²
可能な用途:
組み立て、顧客サービス、機械の修理などのタスクが完了するまでの時間をモデル化するために使用されます。
コメント:
γ = 0のとき、この分布はm-Erlang(β)分布と呼ばれます。
exponential( γ, β )とerlang( γ, β, 1 )分布は同一です。
正の整数mについて、gamma( γ, β, m )とerlang( γ, β, m )分布は同一です。
例
double servicetime = erlang(60, 2, 4, 5);
変数servicetimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4のアーラン分布に従い、5番目の乱数ストリームを使用して設定されます。平均値は100 + (2*4) = 108です。
変数servicetimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4のアーラン分布に従い、5番目の乱数ストリームを使用して設定されます。平均値は100 + (2*4) = 108です。
exponential (num location, num scale [, num stream])
指数分布からランダムなサンプルを返す
説明
exponential( γ, β, stream)は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ, ∞ )
平均値 = γ + β
分散 = β²
可能な用途:
多くの場合、顧客や、顧客からシステムへの注文の連続的なストリームの到着間の時間をモデル化するために使用されます。また、機械的装置の故障の間隔をモデル化するための一般的な分布でもあります。
コメント:
平均値より小さい変量は、平均値より大きい変量よりもはるかに頻繁に発生します。
指数分布は、メモリなしのプロパティで完全に独立した変量を生成する唯一の連続分布です。
位置パラメータ(γ)が0に設定されている場合、βは平均値となり、分布の範囲は0と無限大の間になります。
exponential( γ, β )とgamma( γ, β, 1 )分布は同一です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ, ∞ )
平均値 = γ + β
分散 = β²
可能な用途:
多くの場合、顧客や、顧客からシステムへの注文の連続的なストリームの到着間の時間をモデル化するために使用されます。また、機械的装置の故障の間隔をモデル化するための一般的な分布でもあります。
コメント:
平均値より小さい変量は、平均値より大きい変量よりもはるかに頻繁に発生します。
指数分布は、メモリなしのプロパティで完全に独立した変量を生成する唯一の連続分布です。
位置パラメータ(γ)が0に設定されている場合、βは平均値となり、分布の範囲は0と無限大の間になります。
exponential( γ, β )とgamma( γ, β, 1 )分布は同一です。
例
exponential(0, 10, 5);
位置0、スケール10(平均値 = 10)の指数分布です。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。
位置0、スケール10(平均値 = 10)の指数分布です。分布から変量を生成するため、FlexSimの5番目の乱数ストリームが使用されます。
exportdataset (node datatree, str filename, num format)
説明
ツリーデータセットを.CSV(カンマ区切り値)形式にエクスポートします。
formatパラメータは次のいずれかです。
1 = テーブル
2 = グラフ
3 = graphxy
これは、importdataset()の逆の機能です。詳細については、importdataset()を参照してください。
formatパラメータは次のいずれかです。
1 = テーブル
2 = グラフ
3 = graphxy
これは、importdataset()の逆の機能です。詳細については、importdataset()を参照してください。
例
exportdataset(so(),"mydataset.csv",1)
extremevalue1a (num location, num scale[, num stream])
extremevalue1a分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、extremevalue1a分布から連続的なランダム変量を生成します。
例
extremevalue1b (num location, num scale[, num stream])
extremevalue1b分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、extremevalue1b分布から連続的なランダム変量を生成します。
例
gamma (num location, num scale, num shape[, num stream])
ガンマ分布からランダムなサンプルを返す
説明
gamma( γ, β, α, stream )は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + αβ
分散 = αβ²
確率密度関数:
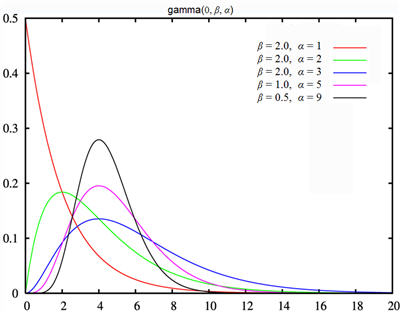
可能な用途:
組み立て、顧客サービス、機械の修理などのタスクが完了するまでの時間をモデル化するために使用されます。
コメント:
exponential( γ, β )とgamma( γ, β, 1 )分布は同一です。
正の整数mについて、gamma( γ, β, m )とerlang( γ, β, m )分布は同一です。
1より小さいshapeの値はほとんど使用されません。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + αβ
分散 = αβ²
確率密度関数:

可能な用途:
組み立て、顧客サービス、機械の修理などのタスクが完了するまでの時間をモデル化するために使用されます。
コメント:
exponential( γ, β )とgamma( γ, β, 1 )分布は同一です。
正の整数mについて、gamma( γ, β, m )とerlang( γ, β, m )分布は同一です。
1より小さいshapeの値はほとんど使用されません。
例
double repairtime = gamma(60, 2, 3.4, 5);
変数repairtimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4のガンマ分布に従い、5番目の乱数ストリームを使用して設定されます。平均値は100 + (2*3.4) = 106.8です。
変数repairtimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4のガンマ分布に従い、5番目の乱数ストリームを使用して設定されます。平均値は100 + (2*3.4) = 106.8です。
geometric (num prob[, num stream])
幾何分布からランダムなサンプルを返す
説明
幾何分布に従い、指定されたパラメータを使用して、離散的な乱数を生成します。
例
getbundlefieldname (node datanode, num fieldnr)
バンドル内のn番目のランク付きフィールド(0から開始)の名前を取得する
説明
バンドル内のn番目のランク付きフィールド(0から開始)の名前を取得します。
例
string fieldname = getbundlefieldname(x, 5);
getbundlefieldnr (node datanode, str fieldname)
バンドルのフィールドのランクを取得する(0から開始)
説明
バンドルのフィールドのランクを取得します(0から開始)。バンドルのフィールドが存在しない場合、-1を返します。
例
int index = getbundlefieldnr(x, "Field Name");
getbundlefieldtype (node datanode, num fieldnr)
ランクfieldnr(0から開始)にあるバンドルフィールドのデータタイプを取得する
説明
ランクfieldnr(0から開始)にあるバンドルフィールドのデータタイプを取得します。利用可能な戻り値は次のとおりです。
BUNDLE_FIELD_TYPE_DOUBLE
BUNDLE_FIELD_TYPE_FLOAT
BUNDLE_FIELD_TYPE_INT
BUNDLE_FIELD_TYPE_STR
BUNDLE_FIELD_TYPE_VARCHAR
BUNDLE_FIELD_TYPE_NODEREF
BUNDLE_FIELD_TYPE_DOUBLE
BUNDLE_FIELD_TYPE_FLOAT
BUNDLE_FIELD_TYPE_INT
BUNDLE_FIELD_TYPE_STR
BUNDLE_FIELD_TYPE_VARCHAR
BUNDLE_FIELD_TYPE_NODEREF
例
int type = getbundlefieldtype(x, 5);
getbundleindexentries (node datanode, str/num field, str/num value)
与えられたフィールドの値が一致するすべての行を取得する
説明
このコマンドが成功した場合、与えられたフィールドに指定の値が含まれているすべてのエントリ(0から開始)を含むintまたはintarrayを返します。失敗した場合、-1を返します。datanodeがバンドルでない、与えられたフィールドがインデックス付きフィールドでない、またはどのフィールドの値も指定された値と一致しない場合、このコマンドは失敗します。インデックス付きフィールドを作成する方法については、addbundlefieldコマンドを参照してください。
例
int entryNr = getbundleindexentries(data, "SKU", "FS2016-BLU");
getbundlenrentries (node datanode)
バンドル内の合計エントリ数を取得する
説明
バンドル内の合計エントリ数を返します。
例
int nrentries = getbundlenrentries(x);
getbundlenrfields (node datanode)
バンドル内の合計フィールド数を取得する
説明
バンドル内の合計フィールド数を返します。
例
int nrfields = getbundlenrfields(x);
getbundlevalue (node datanode, num entrynr, str/num field)
バンドル内で定義されたエントリ(0から開始)およびフィールド(0から開始)の値を取得する
説明
バンドル内で定義されたエントリ(0から開始)およびフィールド(0から開始)の値を返します。
例
string name = getbundlevalue(x, 5, "Object Name");
getdatastat (num stat, num/node nrSamples/parentNode, num sampler [, num p1, num p2, num p3])
説明
データセットの特定の統計を計算して返します。
stat - 次のいずれかの値を指定します。
stat - 次のいずれかの値を指定します。
nrSamples - セットのサンプル数を定義します。
注意:パラメータ2のparentNodeは廃止されました。nrSamplesオプションを使用してください。このオプションは他のものを包含し、より柔軟です。次の機能は廃止されました。
sampler - サンプルのn番目の値を取得する表現。getdatastat(STAT_MEAN, myNode, 0, 0, 0, 0)は、新しいオプションを次のものと併用して表現できます。 getdatastat(STAT_MEAN, myNode.subnodes.length, myNode.subnodes[count].value, 0, 0, 0)どの値が取得されるかを判定するには、countを使用します。いくつかの例を次に示します。
グローバルテーブルGT1の列5にあるすべての値の平均値を計算するには、次のように指定します。
バンドルの「Time」フィールドにあるすべての値の合計を計算するには、次のように指定します。
グローバルテーブルGT1の列5にあるすべての値の平均値を計算するには、次のように指定します。
getdatastat(STAT_MEAN, Table("GT1").numRows, Table("GT1")[count][5])バンドルの「Time」フィールドにあるすべての値の合計を計算するには、次のように指定します。
getdatastat(STAT_SUM, Table("MyBundle").numRows, Table("MyBundle")[count]["Time"])例
getstat (node object, str name, int flag [, var p1, var p2, var p3])
与えられたオブジェクトの統計値を返す
説明
この代わりにObject.statsを使用することをお勧めします。与えられたオブジェクトから指定された統計を取得します。
name - 統計の名前。
flag - 次のいずれかの値を指定します。
p1、p2、p3は、正しい統計を解決するための「要件」を提供します。たとえば、リストには複数のパーティションごとの統計があります。パーティションの統計を取得するには、パーティションIDをp1として渡す必要があります。要件は、取得される統計によって異なります。
また、いくつかの特別な統計名も使用できます。このような名前として、「State」、「Output」、「Input」、「Content」、「Staytime」があります。これらの名前のいずれかを使用すると、オブジェクトの対応する標準の統計がコマンドにより返されます。次に例を示します。
平均状態、平均出力など一部の統計は意味をなさないため、有効な値が返されないことに注意してください。
STAT_TIME_AT_VALUE
STAT_TIME_AT_VALUEにアクセスするには、統計が履歴またはプロファイルデータを追跡している必要があります。これがオブジェクトの標準の「State」統計である場合、FlexSimによってプロファイルデータが自動的に追跡されるため、それ以上の操作は必要ありません。しかし他の統計では、プロファイルや履歴のデータを追跡するため、統計を明示的に「サブスクライブ」する必要があります。履歴データは、値が変更されるごとに、その変更と、変更に対応するシミュレーション時間を記録します。プロファイルデータは、変数がそれぞれの値であった合計時間を記録します。プロファイルデータに有効なのは非負の整数値のみです。
追跡変数をサブスクライブするには、最初にツリー内で追跡変数の統計を見つけます。たとえば「Content」統計なら、通常はobject>stats/stats_contentにあります。次に、function_s(statNode, "addSubscriber", needsHistory, needsProfile, persist)コマンドを呼び出します。needsHistoryおよびneedsProfileパラメータはブール値で、どのデータを追跡するかを指定します。persistはブール値で、それらの統計を以後無期限に追跡するのかどうかを指定します。追跡変数は、必要がない限り余分なデータの追跡を継続しないよう試みます。データへの「継続的な」サブスクライブがある程度の期間存在しなければ、データの記録は停止されます(たとえば、サブスクライバーが存在しないままモデルが5回程度リセットされた場合)。
履歴データを記録することで、STAT_TIME_AT_VALUEにアクセスできるようになります。ただし、STAT_TIME_AT_VALUEを取得するため履歴データを使用するのは、プロファイルデータを追跡するより低速です。履歴データでは、STAT_TIME_AT_VALUEを計算するため履歴の全体を走査する必要があります。これに対してプロファイルデータを追跡すると、値に対応する合計時間がプロファイルデータに直接格納されます。
name - 統計の名前。
function_s(object, "enumerateStatistics", targetNode)を使用して、有効な名前のリストを得られます。オブジェクトで提供される各種の統計の意味は、それぞれのオブジェクトのドキュメントに記載されています。ドキュメントでは、読みやすくするため統計の名前にスペースが含まれていることがあります。これらをgetstat()のnameパラメータとして渡すときは、すべての空白を削除してください。flag - 次のいずれかの値を指定します。
p1、p2、p3は、正しい統計を解決するための「要件」を提供します。たとえば、リストには複数のパーティションごとの統計があります。パーティションの統計を取得するには、パーティションIDをp1として渡す必要があります。要件は、取得される統計によって異なります。
また、いくつかの特別な統計名も使用できます。このような名前として、「State」、「Output」、「Input」、「Content」、「Staytime」があります。これらの名前のいずれかを使用すると、オブジェクトの対応する標準の統計がコマンドにより返されます。次に例を示します。
getstat(object, "Output", STAT_CURRENT)- オブジェクトの現在の(合計)出力を返す(object.stats.outputと同じ)getstat(object, "Content", STAT_AVERAGE) - オブジェクトの平均コンテンツを返すgetstat(object, "State", STAT_CURRENT, 0) - オブジェクトの現在の状態を返す(object.stats.state().valueと同じ)getstat(object, "State", STAT_TIME_AT_VALUE, 0, STATE_IDLE) - オブジェクトの合計アイドル時間を返す(0は状態プロファイル、すなわちデフォルト状態プロファイルを示す)getstat(object, "Staytime", STAT_MAX) - オブジェクトで記録された最大滞在時間を返す平均状態、平均出力など一部の統計は意味をなさないため、有効な値が返されないことに注意してください。
STAT_TIME_AT_VALUE
STAT_TIME_AT_VALUEにアクセスするには、統計が履歴またはプロファイルデータを追跡している必要があります。これがオブジェクトの標準の「State」統計である場合、FlexSimによってプロファイルデータが自動的に追跡されるため、それ以上の操作は必要ありません。しかし他の統計では、プロファイルや履歴のデータを追跡するため、統計を明示的に「サブスクライブ」する必要があります。履歴データは、値が変更されるごとに、その変更と、変更に対応するシミュレーション時間を記録します。プロファイルデータは、変数がそれぞれの値であった合計時間を記録します。プロファイルデータに有効なのは非負の整数値のみです。
追跡変数をサブスクライブするには、最初にツリー内で追跡変数の統計を見つけます。たとえば「Content」統計なら、通常はobject>stats/stats_contentにあります。次に、function_s(statNode, "addSubscriber", needsHistory, needsProfile, persist)コマンドを呼び出します。needsHistoryおよびneedsProfileパラメータはブール値で、どのデータを追跡するかを指定します。persistはブール値で、それらの統計を以後無期限に追跡するのかどうかを指定します。追跡変数は、必要がない限り余分なデータの追跡を継続しないよう試みます。データへの「継続的な」サブスクライブがある程度の期間存在しなければ、データの記録は停止されます(たとえば、サブスクライバーが存在しないままモデルが5回程度リセットされた場合)。
履歴データを記録することで、STAT_TIME_AT_VALUEにアクセスできるようになります。ただし、STAT_TIME_AT_VALUEを取得するため履歴データを使用するのは、プロファイルデータを追跡するより低速です。履歴データでは、STAT_TIME_AT_VALUEを計算するため履歴の全体を走査する必要があります。これに対してプロファイルデータを追跡すると、値に対応する合計時間がプロファイルデータに直接格納されます。
例
getstream (node object)
オブジェクトと関連付けられている固有のランダムストリームを返す
説明
オブジェクトと関連付けられている固有のランダムストリームを返します。
オブジェクトのstream属性に格納されている数値を返します。オブジェクトにまだ独自のstream属性が存在しない場合、またはstream属性が0の場合、FlexSimは属性をアサートし、固有のストリーム番号を割り当てます。関数に渡されたオブジェクトにオブジェクトデータが存在しない場合、サブノードに固有のストリームを格納します。このサブノードはモデルのリセット時に破棄され、モデルの実行時に必要に応じて再割り当てされます。
割り当てられたストリームはストリーム101から始まり、割り当てごとに番号が増やされます。
オブジェクトのstream属性に格納されている数値を返します。オブジェクトにまだ独自のstream属性が存在しない場合、またはstream属性が0の場合、FlexSimは属性をアサートし、固有のストリーム番号を割り当てます。関数に渡されたオブジェクトにオブジェクトデータが存在しない場合、サブノードに固有のストリームを格納します。このサブノードはモデルのリセット時に破棄され、モデルの実行時に必要に応じて再割り当てされます。
割り当てられたストリームはストリーム101から始まり、割り当てごとに番号が増やされます。
例
uniform(0, 1, getstream(current))
graphtohistogram (obj graph, obj histogram, num start, num end, num res, num xyformat)
説明
開発者向けです。値のリストからヒストグラムデータを生成します。このコマンドは、グラフにより与えられる出現テーブルに基づいて、ノードのヒストグラム内にヒストグラムを生成します。主に、オブジェクトによって内部的に使用されます。ヒストグラムの開始値はstartで指定されます。ヒストグラムの終了値はendで指定されます。ヒストグラムのバケットの数はresで指定されます。xyformatが0なら、グラフはy形式の出現テーブルと想定されます。xyformatが1なら、グラフはxy形式の出現テーブルと想定されます。makehisto()と同様です。これらの類似性の詳細については、makehisto()を参照してください。
例
graphtohistogram(so(),so().next,1,10,5,0)
hypergeometric (num trials, num successes, num size[, num stream])
超幾何分布からランダムなサンプルを返す
説明
hypergeometric( t, m, n, stream )は離散的な確率分布で、サイズnの集団に成功状態が正確にm個含まれている場合、その集団から置き換えなしにt回引き出しを行った時の成功の数を表すために使用されます。
例
importdataset (obj datatree, str filename, num format)
説明
カンマ区切り値(CSV)ファイルからツリーデータセットをインポートします。datatreeはデータをインポートする先のノードです。インポートが可能な形式は3つです。formatが1なら、データはテーブルとしてインポートされ、datatreeの各サブノードはテーブルの行、各行のサブノードはテーブルのセルとなります。これは、importtable()コマンドを使用するのと同じ動作です。formatが2なら、データは単純な連続データとしてインポートされます。csvファイルは1列と見なされ、各行の値はdatatreeのサブノードにインポートされます。formatが3なら、データはx、yペアの連続としてインポートされます。csvファイルは2列と見なされます。csvファイルの行1列1はdatatreeのサブノード1、行1列2はサブノード2、行2列1はサブノード3の順にインポートされます。
例
importdataset(so(),"C:\\mydataset.csv",1)
inversegaussian (num location, num scale, num shape[, num stream])
逆ガウス分布からランダムなサンプルを返す
説明
inversegaussian( γ, β, α, stream )は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + β
分散 = β³⁄α
確率密度関数:
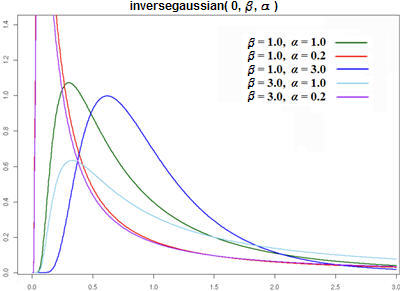
可能な用途:
一部のタスクを完了するための時間をモデル化するために使用されます。
コメント:
inversegaussian( γ, 1, α )とwald( γ, α )分布は同一です。
γが無限大に近づくと、分布は正規(ガウス)分布に近くなります。
βパラメータは傾斜と尖度(幅)に影響するため、shapeパラメータの要素を持ちます。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + β
分散 = β³⁄α
確率密度関数:

可能な用途:
一部のタスクを完了するための時間をモデル化するために使用されます。
コメント:
inversegaussian( γ, 1, α )とwald( γ, α )分布は同一です。
γが無限大に近づくと、分布は正規(ガウス)分布に近くなります。
βパラメータは傾斜と尖度(幅)に影響するため、shapeパラメータの要素を持ちます。
例
double repairtime = inversegaussian(60, 2, 4, 5);
変数repairtimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4の逆ガウス分布に従い、5番目の乱数ストリームを使用して設定されます。
変数repairtimeは、位置パラメータが60、スケールパラメータが2、形状パラメータが4の逆ガウス分布に従い、5番目の乱数ストリームを使用して設定されます。
inverseweibull (num location, num scale, num shape[, num stream])
逆ワイブル分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、逆ワイブル分布から連続的なランダム変量を生成します。
例
invertedweibull (num location, num scale, num shape[, num stream])
逆ワイブル分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、逆ワイブル分布から連続的なランダム変量を生成します。
例
johnsonbounded (num min, num max, num shape1, num shape2[, num stream])
ジョンソン有界分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、ジョンソン有界分布から連続的なランダム変量を生成します。
例
johnsonunbounded (num location, num scale, num shape1, num shape2[, num stream])
ジョンソン非有界分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、ジョンソン非有界分布から連続的なランダム変量を生成します。
例
laplace (num location, num scale[, num stream])
ラプラス分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、ラプラス分布から連続的なランダム変量を生成します。
例
logarithmic (num theta[, num stream])
対数分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、対数分布から離散的なランダム変量を生成します。
例
logistic (num location, num scale[, num stream])
ロジスティック分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、ロジスティック分布から連続的なランダム変量を生成します。
例
loglaplace (num location, num scale, num shape[, num stream])
対数ラプラス分布からランダムなサンプルを返す
説明
loglaplace( γ, β, α, stream )は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + βα²⁄ ( α²− 1) (α > 1の場合)
分散 = β²α² ( 2α² + 1 ) ⁄ ( α² - 1 )² ( α² - 4 ) (α > 2の場合)
確率密度関数:
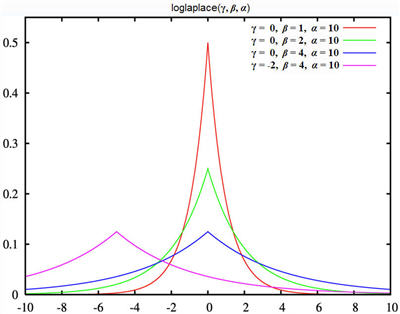
可能な用途:
処理時間の定義に稀に使用されます。
コメント:
この分布は二重指数分布とも呼ばれます。これは、密度曲線が本質的に2つの指数曲線をつなげたものとなるためです。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + βα²⁄ ( α²− 1) (α > 1の場合)
分散 = β²α² ( 2α² + 1 ) ⁄ ( α² - 1 )² ( α² - 4 ) (α > 2の場合)
確率密度関数:

可能な用途:
処理時間の定義に稀に使用されます。
コメント:
この分布は二重指数分布とも呼ばれます。これは、密度曲線が本質的に2つの指数曲線をつなげたものとなるためです。
例
loglaplace(0, 2, 8, 5);
位置パラメータが0、スケールパラメータが2、形状パラメータが8の対数ラプラス分布に従い、5番目の乱数ストリームを使用します。
位置パラメータが0、スケールパラメータが2、形状パラメータが8の対数ラプラス分布に従い、5番目の乱数ストリームを使用します。
loglogistic (num location, num scale, num shape[, num stream])
対数ロジスティック分布からランダムなサンプルを返す
説明
loglogistic(γ, β, α, stream)は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( 0, ∞ )。
αは形状パラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ, ∞ )
平均値 = γ + β(π⁄α)csc(π⁄α) (α > 1の場合)
分散 = β²(π⁄α){2csc(2π⁄α) − (π⁄α)[csc(π⁄α)]²} (α > 2の場合)
可能な用途:
一部のタスクを実行するための時間をモデル化するために使用されます。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( 0, ∞ )。
αは形状パラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ, ∞ )
平均値 = γ + β(π⁄α)csc(π⁄α) (α > 1の場合)
分散 = β²(π⁄α){2csc(2π⁄α) − (π⁄α)[csc(π⁄α)]²} (α > 2の場合)
可能な用途:
一部のタスクを実行するための時間をモデル化するために使用されます。
例
loglogistic(0, 1, 2, 5);
位置(シフト)が0、スケールが1、形状係数が2の対数ロジスティック分布に従い、5番目の乱数ストリームを使用します。
位置(シフト)が0、スケールが1、形状係数が2の対数ロジスティック分布に従い、5番目の乱数ストリームを使用します。
lognormal2 (num location, num scale, num shape[, num stream])
対数正規分布からランダムなサンプルを返す
説明
lognormal()とlognormal2()は類似の関数ですが、パラメータの定義が異なります。lognormal()は、wikipediaや他のサイトで定義されているパラメータ定義を使用します。lognormal2()は、Expertfitの最新版で定義されているパラメータを使用します。本質的に、パラメータは次のように変換できます。
lognormal( location, normalmean, normalstdev ) = lognormal2( location, Math.exp( normalmean ), normalstdev )
lognormal2( location, scale, shape ) = lognormal( location, Math.log( scale ), shape ) (Math.exp(x)はeのx乗で、Math.log(x)はxの自然対数です)。
正しい分布を使用していることを確認してください。誤った分布を使用すると、不正確なシミュレーション結果が返されることがあります。
lognormal( location, normalmean, normalstdev ) = lognormal2( location, Math.exp( normalmean ), normalstdev )
lognormal2( location, scale, shape ) = lognormal( location, Math.log( scale ), shape ) (Math.exp(x)はeのx乗で、Math.log(x)はxの自然対数です)。
正しい分布を使用していることを確認してください。誤った分布を使用すると、不正確なシミュレーション結果が返されることがあります。
例
double cycletime = lognormal2(0, 29.8, 0.31, 5);
cycletime変数を、位置パラメータが0、スケールパラメータが29.8、形状パラメータが0.31のlognormal2分布に従い、5番目の乱数ストリームを使用して設定します。
cycletime変数を、位置パラメータが0、スケールパラメータが29.8、形状パラメータが0.31のlognormal2分布に従い、5番目の乱数ストリームを使用して設定します。
makehisto (obj datalist, obj histocontainer, num nrofbuckets)
説明
開発者向けです。データリストからヒストグラム構造を構築し、指定された数のバケットとして宛先のコンテナノードに格納します。これはgraphtohistogram()とほぼ同じですが、このコマンドはより完全な構造を作成します。この代わりにオペレーターを示すには、FlexSimオブジェクトの属性ツリーを表示します。makehistoコマンドはobject>stats/staytime/staytimehistoの完全な構造を作成するのに対して、graphtohistogramはobject>stats/staytime/staytimehisto/dataのみを書き込みます。またmakehistoでは、標準のyデータシリーズ構造を想定し、datalistの各サブノードはそれぞれ独自のデータポイントです(x/y値としてペアになりません)。
例
makehisto(c.find("@>objectfocus+"), c.find(">histogram"), 20)
negbinomial (num successes, num prob[, num stream])
負の二項分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、負の二項分布から離散的なランダム変量を生成します。
例
normal (num mean, num stddev[, num stream])
正規分布からランダムなサンプルを返す
説明
normal(μ, σ, stream)は非有界の連続的な確率分布です。
入力:
μは位置パラメータです ∈ ( - ∞, ∞ )。
σはスケールパラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( - ∞, ∞ )
平均値 = μ
分散 = σ²
確率密度関数:
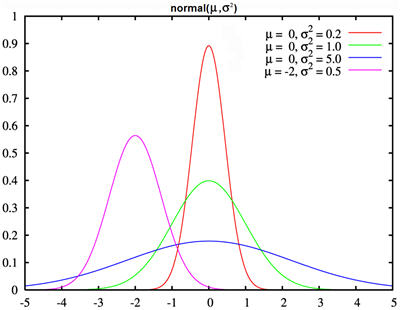
可能な用途:
多数の部品に機械で開けられた穴の直径など、各種の誤差をモデル化するために使用されます。実際のプロセスは、このような対称的分布に従わないことが多いため、この分布はシミュレーションではあまり使用されません。
コメント:
正規分布は完全に対称形で、平均値より小さい値は平均値より大きい値と同じ確率で出現します。正規分布では最頻値と平均値は同一です。この分布を使用するときは、負の値が返される可能性があるため、以下の例で示すように分布を0で切り捨てることが必要な場合があることに注意してください。
入力:
μは位置パラメータです ∈ ( - ∞, ∞ )。
σはスケールパラメータです( 0, ∞ )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( - ∞, ∞ )
平均値 = μ
分散 = σ²
確率密度関数:

可能な用途:
多数の部品に機械で開けられた穴の直径など、各種の誤差をモデル化するために使用されます。実際のプロセスは、このような対称的分布に従わないことが多いため、この分布はシミュレーションではあまり使用されません。
コメント:
正規分布は完全に対称形で、平均値より小さい値は平均値より大きい値と同じ確率で出現します。正規分布では最頻値と平均値は同一です。この分布を使用するときは、負の値が返される可能性があるため、以下の例で示すように分布を0で切り捨てることが必要な場合があることに注意してください。
例
double thickness = Math.max(0.001, normal(5, 1.2));
thicknessは、平均値5、標準偏差1.2で、0.001より小さい値を切り捨てた正規分布に設定されます。乱数ストリームが宣言されていないので、分布から変量を生成するため、デフォルトである0番目のストリームが使用されます。
thicknessは、平均値5、標準偏差1.2で、0.001より小さい値を切り捨てた正規分布に設定されます。乱数ストリームが宣言されていないので、分布から変量を生成するため、デフォルトである0番目のストリームが使用されます。
pareto (num min, num scale[, num stream])
パレート分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、パレート分布から連続的なランダム変量を生成します。
例
pearsont5 (num location, num scale, num shape[, num stream])
ピアソンt 5分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、パーソン-T5分布から連続的なランダム変量を生成します。
例
pearsont6 (num location, num scale, num shape1, num shape2[, num stream])
ピアソンt 6分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、パーソン-T6分布から連続的なランダム変量を生成します。
例
poisson (num mean[, num stream])
ポアソン分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、ポアソン分布から連続的なランダム変量を生成します。
例
qstudentt (num confidence [0.9/0.95/0.99], num degreesoffreedom)
説明
開発者向けです。与えられた信頼水準と自由度について、スチューデントのt分布の値の数量を返します。
例
qstudentt(0.95, nrofsamples - 1)
randantithetic (num on/off)
説明
数値ストリームを逆転します。このコマンドを使用すると、乱数ストリームが、デフォルトの0から1までではなく、1と0の間の数値を生成するように切り替えできます。このコマンドは、乱数がモデルの結果に大きな影響を及ぼすかどうかを判定するために便利です。また、大規模なモデルで実験を行うとき、適切な統計的サンプリングに必要な回数だけモデルを実行するための十分な時間がない場合にも便利です。モデルを1回だけ普通に実行してから、対称形でもう1回実行すると、2つの正反対の結果を得ることができます。これら2つの結果を平均化すると、モデルの実行ごとに逆転サンプリングなしでランダムストリームジェネレータを使用した場合より、多少良好な近似値を得ることができます。
例
randantithetic(1);
randinit (num stream, num seedvalue[, num seedvalue2, num seedvalue3, num seedvalue4, num seedvalue5, num seedvalue 6])
ランダムストリームを初期化する
説明
乱数ストリームの最初の値をseedvalueに設定して初期化します。利用可能な乱数ストリームの数は無制限ですが、FlexSimアプリケーションが開始するときには0~99番の100個のストリームのみが初期化されます。新しいストリームを作成するには、新しいストリームにrandinit()コマンドを実行します。たとえば、randinit(105, 7628912)を実行すると、ストリーム番号105が存在していなければ作成され、初期シード値が7628912に設定されます。
[統計]メニューで[ランダムストリームを繰り返す]が選択されている場合、モデルがリセットされるたびに0から99までのストリームが、各ストリームのデフォルトのシード値を使用して自動的に初期化されます。100番およびそれ以降のストリームについてランダムストリームを繰り返すには、randinit()コマンドを使用して初期シード値を設定する必要があります。乱数ストリームのseedvalueには、任意の正の整数を渡すことができます。ランダムストリーム0~99のseedvalueとして0を渡すと特別なケースとなり、デフォルトのシード値で初期化されます。
seedvalueの2から6までは、FlexSimの結合MRG乱数ジェネレータを使用している場合のみ使われます。このジェネレータを有効にするには、モデルを開くときにmaintenance(49,1)を呼び出します。
[統計]メニューで[ランダムストリームを繰り返す]が選択されている場合、モデルがリセットされるたびに0から99までのストリームが、各ストリームのデフォルトのシード値を使用して自動的に初期化されます。100番およびそれ以降のストリームについてランダムストリームを繰り返すには、randinit()コマンドを使用して初期シード値を設定する必要があります。乱数ストリームのseedvalueには、任意の正の整数を渡すことができます。ランダムストリーム0~99のseedvalueとして0を渡すと特別なケースとなり、デフォルトのシード値で初期化されます。
seedvalueの2から6までは、FlexSimの結合MRG乱数ジェネレータを使用している場合のみ使われます。このジェネレータを有効にするには、モデルを開くときにmaintenance(49,1)を呼び出します。
例
例1:
randinit(5, 73241);
FlexSimの5番のランダムストリームを、シード値73241で初期化します。
例2:
randinit(2,0);
for(int i = 100; i <= 199; i++)
{
randinit(i, realtime(1) * uniform(0, 1, 2));
}
標準のストリーム番号2をデフォルトのシード値で初期化してから、ループを100回繰り返し実行して100番から199番までのストリームを(必要なら)作成し、それぞれの初期シード値を、ストリーム2からプルされた乱数と、リアルクロックの現在の秒数との積に設定します。
randinit(5, 73241);
FlexSimの5番のランダムストリームを、シード値73241で初期化します。
例2:
randinit(2,0);
for(int i = 100; i <= 199; i++)
{
randinit(i, realtime(1) * uniform(0, 1, 2));
}
標準のストリーム番号2をデフォルトのシード値で初期化してから、ループを100回繰り返し実行して100番から199番までのストリームを(必要なら)作成し、それぞれの初期シード値を、ストリーム2からプルされた乱数と、リアルクロックの現在の秒数との積に設定します。
randnext (num stream)
説明
開発向けです。ストリームから次の乱数を返します。このコマンドは、確率分布関数からランダムなサンプルをプルするために使用されます。
例
randnext(1);
ストリームジェネレータの1番に関連付けられている乱数ストリームの、次の乱数を取得します。
ストリームジェネレータの1番に関連付けられている乱数ストリームの、次の乱数を取得します。
randomwalk (num location, num scale, num shape[, num stream])
説明
定義されたパラメータに従い、ランダムウォーム分布から連続的なランダム変量を生成します。
例
randstate (num stream[, seednr])
乱数ストリームの現在の状態値を取得する
説明
指定された乱数ストリームの現在の状態値を返します。この状態値をrandinit()コマンドのシード値として使用すると、保存した状態モデルを初回実行時の乱数ストリームと同じ時点から再開できます。
seednrは、FlexSimの結合MRC乱数ジェネレータを使用している場合のみ必要となり、どのシード値の状態を取得するのかを値1~6で定義します。結合MRGの使用法については、randinit()を参照してください。
seednrは、FlexSimの結合MRC乱数ジェネレータを使用している場合のみ必要となり、どのシード値の状態を取得するのかを値1~6で定義します。結合MRGの使用法については、randinit()を参照してください。
例
int curstate = randstate(5);
変数curstateを、現在のランダム整数値ストリームの5番に設定します。
変数curstateを、現在のランダム整数値ストリームの5番に設定します。
removebundleentry (node datanode, int entrynum)
バンドルのエントリentrynum(0から開始)を削除する
説明
バンドルのエントリentrynum(0から開始)を削除します。
例
removebundleentry(x, 2);
removefirstbundleentry (node datanode)
バンドルの最初のエントリを削除する
説明
バンドルの最初のエントリを削除します。履歴データのメモリフットプリントの管理に使用します。
例
removefirstbundleentry(x);
removelastbundleentry (node datanode)
バンドルの最後のエントリを削除する
説明
バンドルの最後のエントリを削除します。
例
removefirstbundleentry(x);
setbundlevalue (node datanode, num entrynr, str/num field, num/str val)
バンドルのエントリ(0から開始)およびフィールド(0から開始)の値を設定する
説明
バンドルで定義されたエントリ(0から開始)およびフィールド(0から開始)の値を設定します。
例
setbundlevalue(x, 5, "Object Name", current.name);
triangular (num min, num max, num mode[, num stream])
三角分布からランダムなサンプルを返す
説明
定義されたパラメータに従い、三角分布から連続的なランダム変量を生成します。
例
uniform (num min, num max[, num stream])
minとmaxの間のランダムな数値を返す
説明
uniform( a, b, stream )は有界の連続的な確率分布です。
入力:
aおよびbは実数で、a < bです。
aは、最小変量を定義する位置パラメータです。
bは、最大数量を定義します。
b−aがスケールパラメータです。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = [ a, b ]
平均値 = ( a + b ) ⁄ 2
分散 = ( b−a )²⁄ 12
可能な用途:
aとbとの間でランダムに分布し、他の特性がほぼ未知の値を概算するため使用されます。
コメント:
a、b、またはその間に存在する任意の実数値が等しい確率で返されます。
uniform(0, 1)分布は、他のすべての分布からランダムな変量を生成するための基本的なもので、0と1の間(両端を含む)のランダムな値の連続的なセットを返します。
入力:
aおよびbは実数で、a < bです。
aは、最小変量を定義する位置パラメータです。
bは、最大数量を定義します。
b−aがスケールパラメータです。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = [ a, b ]
平均値 = ( a + b ) ⁄ 2
分散 = ( b−a )²⁄ 12
可能な用途:
aとbとの間でランダムに分布し、他の特性がほぼ未知の値を概算するため使用されます。
コメント:
a、b、またはその間に存在する任意の実数値が等しい確率で返されます。
uniform(0, 1)分布は、他のすべての分布からランダムな変量を生成するための基本的なもので、0と1の間(両端を含む)のランダムな値の連続的なセットを返します。
例
uniform(12.3, 27.5, 3);
最小が12.3、最大が27.5の一様分布から、乱数ストリーム3を使用してランダムな変量を生成します。
最小が12.3、最大が27.5の一様分布から、乱数ストリーム3を使用してランダムな変量を生成します。
weibull (num location, num scale, num shape[, num stream])
ワイブル分布からランダムなサンプルを返す
説明
weibull( γ, β, α, stream )は非負の連続的な確率分布です。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + ( β⁄α ) Γ(1 ⁄α)、ここでΓ()はガンマ関数。
分散 = ( β²⁄α ) { 2Γ(2 ⁄α) − 1 ⁄α [ Γ(1 ⁄α) ] ² }
確率密度関数:
可能な用途:
ワイブル分布は、形状係数に応じて多くの異なる形状が存在し得るため、十分なデータを利用できない場合によく使用されます。機器の障害の時間間隔や、手動の作業を完了するための時間を表すため、非常に一般的に使用される分布です。
コメント:
weibull( γ, β, 1 )とexponential( γ, β )分布は同一です。
weibull( γ, β, 2 )とrayleigh( γ, β )分布は同一です。
ワイブル分布は、α > 3.6なら左に傾きます。
入力:
γは位置パラメータです ∈ ( - ∞, ∞ )。
βはスケールパラメータです( β > 0 )。
αは形状パラメータです( α > 0 )。
streamは、FlexSimの乱数ストリーム{0,1,2,...}のいずれかへの参照です。
出力:
範囲 = ( γ , ∞ )
平均値 = γ + ( β⁄α ) Γ(1 ⁄α)、ここでΓ()はガンマ関数。
分散 = ( β²⁄α ) { 2Γ(2 ⁄α) − 1 ⁄α [ Γ(1 ⁄α) ] ² }
確率密度関数:

可能な用途:
ワイブル分布は、形状係数に応じて多くの異なる形状が存在し得るため、十分なデータを利用できない場合によく使用されます。機器の障害の時間間隔や、手動の作業を完了するための時間を表すため、非常に一般的に使用される分布です。
コメント:
weibull( γ, β, 1 )とexponential( γ, β )分布は同一です。
weibull( γ, β, 2 )とrayleigh( γ, β )分布は同一です。
ワイブル分布は、α > 3.6なら左に傾きます。
例
weibull(0, 2, 3, 5);
位置パラメータが0、スケールパラメータが2、形状パラメータが3のワイブル分布に従い、5番目の乱数ストリームを使用します。
位置パラメータが0、スケールパラメータが2、形状パラメータが3のワイブル分布に従い、5番目の乱数ストリームを使用します。
文字列
文字列、文字列の操作、文字列の比較に関連するコマンド。
asciistr (str string [, num index])
説明
このコマンドは、文字列の指定されたインデックス(0から開始)にある文字のascii値を返します。indexが指定されていない場合、文字列の最初の文字が使用されます。
例
asciistr("fred",1)は、「r」のascii値である114を返します。
cdir ()
説明
FlexSimのインストールディレクトリのパスを文字列として返します。
例
string userpath = cdir(); 標準のインストールなら、C:\Program Files\Flexsim3\を返します。
currentfile ()
現在開いているモデルのパスを取得する
説明
現在開いているモデルのパスを返します。
例
currentfile();
documentsdir ()
現在アクティブなユーザーのMy Documents内にあるFlexSim Projectsフォルダのフルパスを取得する
説明
現在アクティブなユーザーのMy Documents内にあるFlexSim Projectsフォルダのフルパスを返します。
例
documentsdir()
executestring (str thestring[, node c, node i, obj eventdata])
文字列をflexscriptとして実行する
説明
与えられた文字列をflexscriptとして実行します。パラメータ2~4はexecutefsnodeと同じです。
例
executestring("profileevents()");
getdirbrowse (str initialdir, str message, node result)
ディレクトリ選択用のブラウザーウィンドウを開く
説明
ディレクトリ選択用のブラウザーウィンドウを開きます。destnodeには文字列データが必要で、ディレクトリのパスはそのテキストに書き込まれます。
例
getdirbrowse(documentsdir, "A folder", destnode)
getpath (str truncatedpath)
切り捨てられたパスのフルファイルパスを返す
説明
切り捨てられた、または相対のファイルパスを受け取り、フルファイルパスを返します。
例
string fullpath = getpath("fs3d\\texturebox.wrl");
modeldir ()
現在開いているモデルのディレクトリのパスを取得する
説明
現在開いているモデルのディレクトリパスを返します。
例
modeldir();
pdir ()
説明
このコマンドは、ハードドライブ上でのFlexSimプログラムディレクトリのパスを含む文字列を返します。
例
string flexpath = pdir();
flexpathを、FlexSimのプログラムディレクトリに設定します。一般的なインストールでは、C:\Program Files\FlexSim7\program\が文字列として返されます。
flexpathを、FlexSimのプログラムディレクトリに設定します。一般的なインストールでは、C:\Program Files\FlexSim7\program\が文字列として返されます。
pfile ()
説明
開発者向けです。FlexSimアプリケーションの開始に使用されたコマンドラインの末尾に付加されていた文字列を返します。
例
FlexSimが次のコマンドラインで開始された場合
"C:\Program Files\Flexsim7\program\flexsim.exe" "mymodel.fsm"
pfile()を呼び出すと、「mymodel.fsm」が文字列として返されます。
"C:\Program Files\Flexsim7\program\flexsim.exe" "mymodel.fsm"
pfile()を呼び出すと、「mymodel.fsm」が文字列として返されます。
programdatadir ()
FlexSimがプログラムデータを格納するディレクトリのフルパスを取得する
説明
FlexSimがヘルプドキュメントなどのプログラムデータを格納するディレクトリのフルパスを返します。
例
programdatadir()は、「C:\ProgramData\Flexsim\Flexsim7\」のような文字列を返します。
replacedata_n (obj startnode, num value, num replacement)
説明
開発者向けです。startnodeの下にある、一致する数値データを検索/置換します。数値データのノードのみが検索されます。見つかった一致の総数を返します。
例
replacedata_n(main(),25,42)
replacedata_s (obj startnode, str string, str replacement[, num replication])
説明
開発者向けです。startnodeの下にある文字列データの一致を検索し、replacement文字列に置き換えます。結果は出力コンソールに表示されます。この関数は部分文字列を認識して置き換えます。検索では大文字と小文字が区別されます。replicationは現在のところ使用されていません。searchdata_s()を参照してください。見つかった一致の総数を返します。
例
replacedata_s(main(),"jack","john")
replacename (obj startnode, str searchname, str replacement)
説明
開発者向けです。startnodeの下にあり、searchnameと一致することが見つかった、すべてのノード名を置き換えます。この関数では正確な一致が必要で、部分文字列は認識されません。見つかった一致の総数を返します。
例
replacename(main(),"jack","john")
searchdata_n (obj startnode, num val)
説明
開発者向けです。startnodeの下にある、一致する数値データを検索します。数値データのノードのみが検索されます。結果は出力コンソールに表示されます。見つかった一致の総数を返します。
例
searchdata_n(main(),25)
searchdata_s (obj startnode, str string [, num replication])
説明
開発者向けです。startnodeの下にある、一致する文字列データを検索します。結果は出力コンソールに表示されます。この関数は部分文字列を認識し、どのノードに何個の部分文字列が含まれているかをレポートします。検索では大文字と小文字が区別されます。replicationは現在のところ使用されていません。見つかった一致の総数を返します。
例
searchdata_s(main(),"glVertex()",1)
searchname (obj startnode, str searchname)
説明
開発者向けです。startnodeの下にある、一致する名前を検索します。結果は出力コンソールに表示されます。検索では大文字と小文字が区別されます。見つかった一致の総数を返します。
例
searchname(main(),"FixedResource")
strascii (num asciivalue)
説明
このコマンドは、ascii値に対応する文字を含む文字列を返します。
例
strascii(91) + "alert(" + strascii(34) + "Hello There" + strascii(34) + ")" + strascii(93);
次のフレーズを含む文字列を返します: [alert("Hello There")]
次のフレーズを含む文字列を返します: [alert("Hello There")]
stringtoken (str token, str delimit)
文字列内の次のトークンを検索する
説明
文字列内の次のトークンを検索します。最初のパラメータは、区切られたトークンを含む文字列です。2番目のパラメータは、区切り文字のセットを持つ文字列です。C++では、strtok()と同じように動作します。
例
string token = "Jacob,Emma,Michael,Isabella,Ethan";
string name = stringtoken(token,",");
while(stringlen(name)>0)
{
pt(name);pr();
name = stringtoken(NULL,",");
}
リストに含まれている名前を、それぞれ別の行として出力コンソールに表示します。
string name = stringtoken(token,",");
while(stringlen(name)>0)
{
pt(name);pr();
name = stringtoken(NULL,",");
}
リストに含まれている名前を、それぞれ別の行として出力コンソールに表示します。
tostring (thing)
説明
開発者向けです。pchar文字列としてアサートします。数値valをタイプchar*としてアサートします。C++でのみ実際の役割を果たしますが、Flexscriptでも安全に使用できます。
例
tostring(eventdata)
truncatemediapath (str path)
説明
渡されたファイルのフルパスに基づいて、切り捨てられたメディアパスを返します。このファイルがモデルのディレクトリに相対的に存在していれば、モデルのディレクトリに対する相対パスに切り捨てられます。ファイルの場所がFlexSimのインストールディレクトリに相対的な場合も、切り捨てが行われます。
例
truncatemediapath("C:\\Program Files\\Flexsim4\\fs3d\\texturebox.wrl");
この例は、文字列「fs3d\\texturebox.wrl」を返します。
この例は、文字列「fs3d\\texturebox.wrl」を返します。
userdatadir ()
FlexSimがユーザーデータを格納するディレクトリのフルパスを取得する
説明
FlexSimがグローバル設定やコンパイラー設定などのユーザーデータを格納するディレクトリのフルパスを返します。
例
userdatadir()は、「C:\Users\USERNAME\AppData\Roaming\Flexsim\Flexsim7\」などの文字列を返します。
テーブル
テーブルのデータにアクセス、割り当て、管理するためのコマンド。
exporttable (node table, str filename [, num exportcolumnnames, num exportrownames] )
テーブルを.CSV形式でエクスポートする
説明
テーブルを.CSV(カンマ区切り値)形式でエクスポートします。
例
exporttable(so(),"mytable.csv",1, 1)
so()に割り当てられたテーブルを、行や列のヘッダーも含めてエクスポートします。
so()に割り当てられたテーブルを、行や列のヘッダーも含めてエクスポートします。
importtable (node importnode, str filepath, num importcolheaders, num importrowheaders)
.csvファイルからimportnodeにテーブルデータをインポートする
説明
.csv(カンマ区切り値)ファイルからノードに、テーブルデータをインポートします。
例
importtable(current.labels["data"], "C:/modeldata.csv", 1,1)
TaskExecuterオブジェクト
TaskExecuterオブジェクトとタスクシーケンスに関連するコマンド。
addsphere (obj object, num x, num y, num z, num radius)
説明
開発者向けです。指定されたオブジェクトに、そのオブジェクトに相対的なx、y、z位置で、指定された半径の衝突球を追加します。TaskExecutersでは、ユーザーが衝突球を追加し、オブジェクトの[パラメータ]ウィンドウから衝突球を描画できますが、他のオブジェクトに必要に応じて衝突球を追加し、描画するにはコマンドが必要です。
例
addsphere(Processor1, 2, -1.25, .75, 1);
changetask (obj tasksequence, num taskrank, num type [, obj involved1, obj involved2 , num var1, num var2, num var3, num var4] )
タスクシーケンスのタスクを動的に変更する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。このコマンドを使用して、タスクを動的に変更できます。たとえば、オペレーターがオブジェクトAの代わりにオブジェクトBに移動するよう変更が必要で、そのオペレーターがオブジェクトAに移動するタスクが既に作成済みの場合、このコマンドを使用してタスクを変更できます。
最初のパラメータ(tasksequence)は、タスクを含むタスクシーケンスを指定します。2番目のパラメータ(taskrank)は、タスクシーケンス内でのタスクのランクを指定します。他のすべてのパラメータはinserttaskコマンドと同じです。
このコマンドは、そのタスクがタスクシーケンス内で現在アクティブなタスクでないときのみ実行できます。
最初のパラメータ(tasksequence)は、タスクを含むタスクシーケンスを指定します。2番目のパラメータ(taskrank)は、タスクシーケンス内でのタスクのランクを指定します。他のすべてのパラメータはinserttaskコマンドと同じです。
このコマンドは、そのタスクがタスクシーケンス内で現在アクティブなタスクでないときのみ実行できます。
例
changetask(gettasksequence(current, 0), 4, TASKTYPE_TRAVEL, current.centerObjects[5]);
この例は、currentオブジェクトのアクティブなタスクシーケンスに含まれる4番目のタスクを、currentオブジェクトの5番目のセンターポートに接続されたオブジェクトに移動する移動タスクに変更します。
この例は、currentオブジェクトのアクティブなタスクシーケンスに含まれる4番目のタスクを、currentオブジェクトの5番目のセンターポートに接続されたオブジェクトに移動する移動タスクに変更します。
createcoordinatedtasksequence (obj dispatcher)
新しい空白の調整されたタスクシーケンスを作成する
説明
指定されたディスパッチャーに、新しい空白の調整されたタスクシーケンスを作成します。以後のいずれかの時点で、dispatchcoordinatedtasksequenceを使用する必要があります。
例
createcoordinatedtasksequence(current.centerObjects[1]);
createemptytasksequence (obj dispatcher, num priority, num preempting)
ディスパッチャーのキューに新しいタスクシーケンスを作成し、そのタスクシーケンスへの参照を返す
説明
このコマンドは廃止されました。代わりにTaskSequence.create()を使用してください。dispatcherのタスクシーケンスキューに、空白のタスクシーケンスを作成します。タスクシーケンスの作成後に、inserttaskコマンドを使用してタスクを追加します。タスクシーケンスは、dispatchtasksequenceコマンドでディスパッチされます。このコマンドは、新たに作成されたタスクシーケンスノードへのポインターを返します。preemptingの値は次のいずれかです。
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
0 - PREEMPT_NOT
1 - PREEMPT_ONLY
2 - PREEMPT_AND_ABORT_ACTIVE
3 - PREEMPT_AND_ABORT_ALL
例
createemptytasksequence(current.centerObjects[1], 1, PREEMPT_NOT);
dispatchcoordinatedtasksequence (obj tasksequence)
調整されたタスクシーケンスをディスパッチする
説明
指定の、調整されたタスクシーケンスをディスパッチします。createcoordinatedtasksequence()の後で、必ず呼び出す必要があります。
例
dispatchcoordinatedtasksequence(newts);
dispatchtasksequence (obj tasksequence)
タスクシーケンスをディスパッチし、タスクシーケンスの取り扱い/実行を開始する
説明
このコマンドは廃止されました。代わりにTaskSequence.dispatch()を使用してください。タスクシーケンスを取り扱うdispatcher/taskexecuterに対して、そのタスクシーケンスがどこに存在するかを通知します。createemptytasksequenceコマンドを使用してタスクシーケンスを作成してから、inserttaskコマンドを使用してタスクを追加した後で、dispatchtasksequenceコマンドを使用してタスクシーケンスの処理を開始します。
例
dispatchtasksequence(newtasksequence);
distancetotravel (obj traveler, obj destination)
移動者が目的地に到達するため必要な移動距離を取得する
説明
移動者(オペレーター、トランスポーターなど)が与えられた目的地に到達するため必要な移動距離を返します。オブジェクトがネットワークに接続されている場合、ネットワークに沿った移動距離を返します。
例
distancetotravel(current.centerObjects[1], current);
drawspheres (obj object, obj view)
説明
開発者向けです。指定されたオブジェクトに割り当てられている衝突球を描画します。TaskExecutersでは、ユーザーが衝突球を追加し、オブジェクトの[パラメータ]ウィンドウから衝突球を描画できますが、他のオブジェクトに必要に応じて衝突球を追加し、描画するにはコマンドが必要です。
例
drawspheres(current,view);
freeoperators (obj taskexecuter, obj involved)
involvedに対して動作しているtaskexecuterに接続されているすべてのオペレーターをリリースする
説明
involvedオブジェクトに対して現在動作している、指定されたディスパッチャーに接続されている、すべてのオペレーターをリリースします。このコマンドは、requestoperatorsコマンドまたはutilizeタスクを使用してプロセスに対して呼び出したオペレーターをリリースするとき、トリガーから実行します。最初のパラメータは、解放するオペレーターに接続されているディスパッチャー、またはオペレーター自体です。2番目のパラメータは、適切なオペレーターをリリースするためのキーです。requestoperatorsコマンドを使用してオペレーターを呼び出した場合、freeoperatorsコマンドの2番目のパラメータは、requestoperatorsコマンドの3番目のパラメータと一致する必要があります。オペレータにutilizeタスクを与えた場合、freeoperatorsコマンドの2番目のパラメータは、utilizeタスクのinvolved1パラメータと一致する必要があります。このコマンドは通常、OnProcessFinishやOnSetupFinishなどのトリガーから実行します。詳細については、ユーザーマニュアルのタスクシーケンスについてのセクションを参照してください。
例
freeoperators(current.centerObjects[1], item);
getallocatedfromkey (obj coordtasksequence, num key)
与えられたキーについて、allocateタスクに割り当てられたオブジェクトへの参照を取得する
説明
与えられたキーにより指定されたallocateタスクに割り当てられている、オブジェクトへの参照を返します。
例
treenode allocatedobj = getallocatedfromkey(getcoordinatedtasksequence(current.centerObjects[1], 0), mykey);
getcoordinatedtasksequence (obj dispatcher, num tasksequencerank)
調整されたタスクシーケンスへの参照を取得する
説明
指定されたディスパッチャーのタスクシーケンスキューに含まれている、指定されたランクの割り当て要求と関連付けられている、
調整されたタスクシーケンスへの参照を返します。指定されたランクが0なら、ディスパッチャーが実際にはTaskExecuterであると見なされ、現在割り当てられている、
調整されたタスクシーケンスへの参照を返します。
調整されたタスクシーケンスへの参照を返します。指定されたランクが0なら、ディスパッチャーが実際にはTaskExecuterであると見なされ、現在割り当てられている、
調整されたタスクシーケンスへの参照を返します。
例
treenode coordtasksequence = getcoordinatedtasksequence(current.centerObjects[1], 5);
getcurtask (node tasksequence)
タスクシーケンスの現在のタスク番号を取得する
説明
タスクシーケンスの現在のタスク番号を返します。
例
if(getcurtask(ts) > 5)
pt("The operator has finished the first five tasks");
pt("The operator has finished the first five tasks");
getnroftasks (obj tasksequence)
タスクシーケンスの未完のタスク数を取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。タスクシーケンスでまだ完了していないタスクの数を返します(現在のタスクも含みます)。
例
if(getnroftasks(mytasksequence) > 5)
pt("There are more than 5 tasks in the tasksequence queue.");
pt("There are more than 5 tasks in the tasksequence queue.");
getpreempt (node tasksequence)
タスクシーケンスのプリエンプト値を取得する
説明
タスクシーケンスのプリエンプト値を返します。
可能な値は次のとおりです。
PREEMPT_NOT、
PREEMPT_ONLY、
PREEMPT_AND_ABORT_ACTIVE、
PREEMPT_AND_ABORT_ALL
可能な値は次のとおりです。
PREEMPT_NOT、
PREEMPT_ONLY、
PREEMPT_AND_ABORT_ACTIVE、
PREEMPT_AND_ABORT_ALL
例
if(getpreempt(mytasksequence) == PREEMPT_ONLY)
pt("This tasksequence is a preempting task");
pt("This tasksequence is a preempting task");
getpriority (node tasksequence)
タスクシーケンスの優先度の値を取得する
説明
タスクシーケンスの優先度の値を返します。
例
if(getpriority(mytasksequence) > 5)
pt("This tasksequence has a priority greater than 5.");
pt("This tasksequence has a priority greater than 5.");
gettaskinvolved (obj tasksequence, num taskrank, num involvednum)
タスクシーケンスのタスクに関連する最初または2番目のオブジェクトへの参照を取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskクラスを使用してください。指定されたtasksequenceで、ランクがn番目のタスクに関連する、最初または2番目のオブジェクトへの参照を返します。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが既に完了し、その後で破棄されている
可能性があるためです。3番目のパラメータは、関連オブジェクトのどちらを取得するかを定義します(1または2)。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクの関連が取得されます。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが既に完了し、その後で破棄されている
可能性があるためです。3番目のパラメータは、関連オブジェクトのどちらを取得するかを定義します(1または2)。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクの関連が取得されます。
例
treenode loaditem = getinvolved(gettasksequence(current.centerObjects[1], 0), 2, 1);
gettasksequence (obj dispatcher, num tasksequencerank)
タスクシーケンスへの参照を取得する
説明
このコマンドは廃止されました。代わりに、DispatcherおよびTaskExecuterのクラスメソッドとプロパティを使用してください。指定されたdispatcherのタスクシーケンスキューにある、指定されたランクを持つタスクシーケンスへの参照を返します。
指定されたランクが0なら、このコマンドはディスパッチャーが実際にはTaskExecuterであると想定し、
現在アクティブなタスクシーケンスへの参照を返します。
指定されたランクが0なら、このコマンドはディスパッチャーが実際にはTaskExecuterであると想定し、
現在アクティブなタスクシーケンスへの参照を返します。
例
treenode mytasksequence = gettasksequence(current.centerObjects[1], 5);
gettasksequencequeue (obj dispatcher)
ディスパッチャーのタスクシーケンスキューへの参照を返す
説明
このコマンドは廃止されました。代わりにDispatcherクラスのプロパティを使用してください。指定されたdispatcherのタスクシーケンスキューへの参照を返します。
例
treenode tsqueue = gettasksequencequeue(current.centerObjects[1]);
gettaskstate (obj tasksequence, num taskrank)
タスクシーケンスのランクがtaskrankであるタスクの状態を取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。tasksequenceの、ランクがtaskrankであるタスクの状態を取得します。タスクの状態には次のものがあります。
TASKSTATE_UNFINISHED
TASKSTATE_ACTIVE
TASKSTATE_FINISHED
TASKSTATE_COORDINATED
TASKSTATE_UNFINISHED
TASKSTATE_ACTIVE
TASKSTATE_FINISHED
TASKSTATE_COORDINATED
例
if(gettaskstate(gettasksequence(current.centerObjects[1], 0), 2) == TASKSTATE_ACTIVE)...
gettasktype (obj tasksequence, num taskrank)
tasksequenceの、ランクがtaskrankであるタスクのタスクタイプを取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。指定されたtasksequenceの、ランクがn番目であるタスクのタスクタイプを返します。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが
既に完了し、その後で破棄されている可能性があるためです。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクのタスクタイプが取得されます。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが
既に完了し、その後で破棄されている可能性があるためです。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクのタスクタイプが取得されます。
例
if(gettasktype(gettasksequence(current.centerObjects[1], 0), 2) == TASKTYPE_LOAD)...
gettaskvariable (obj tasksequence, num taskrank, num variablenum)
タスクシーケンスの、ランクがtaskrankであるタスクのタスクシーケンス変数を取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。指定されたtasksequenceの、ランクがn番目のタスクについて、4つのタスク変数のいずれかへの参照を返します。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが既に完了し、その後で破棄されている
可能性があるためです。3番目のパラメータは、どのタスク変数を取得するかを定義します(1~4)。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクのタスク変数が取得されます。
ランキングは、タスクシーケンスが最初に作成されタスクが追加されたときの、タスクの初期ランキングに
基づきます。シミュレーションの特定時点におけるランキングには基づきません。タスクが既に完了し、その後で破棄されている
可能性があるためです。3番目のパラメータは、どのタスク変数を取得するかを定義します(1~4)。
最初のパラメータとしてTaskExecuterへの参照を、2番目のパラメータとして値0を渡すこともでき、
この場合はオブジェクトの現在アクティブなタスクのタスク変数が取得されます。
例
double myvar = gettaskvariable(gettasksequence(current.centerObjects[1], 0), 2, 1);
gettotalnroftasks (obj tasksequence)
タスクシーケンスに追加されたタスクの総数を取得する
説明
このコマンドは廃止されました。代わりに、TaskSequenceおよびTaskSequence.Taskのクラスメソッドとプロパティを使用してください。tasksequenceに追加されたタスクの総数を返します。
例
gettotalnroftasks(mytasksequence)
getutilizedobject (obj dispatcher, obj involved, obj station, num utilizednr)
utilizeタスクを現在実行しているオペレーターへの参照を取得する
説明
give involvedおよびstation変数を持つutilizeタスクを現在実行しているオペレーターへの参照を検索して返します。複数のオペレーターが使用されている場合、utilizednrを使用して、どのオペレーターを参照するのかを指定できます。
例
treenode op = getutilizedobject(current.centerObjects[1], item, current, 1);
insertallocatetask (obj tasksequence, obj dispatcher, num priority, num preempt [, num noblock] )
割り当てタスクを、調整されたタスクシーケンスに挿入する
説明
割り当てタスクを、指定の調整されたタスクシーケンスに挿入します。デフォルトでは、割り当てタスクはブロッキングタスクですが、noblockが1なら、タスクシーケンスの以後の実行は割り当てによりブロックされません。
例
insertallocatetask(newts, current.centerObjects[2], 0, 0);
insertdeallocatetask (obj tasksequence, num allocationkey [, num noblock] )
割り当て解除タスクを、調整されたタスクシーケンスに挿入する
説明
割り当て解除タスクを、指定の調整されたタスクシーケンスに挿入し、allocationkeyで指定されたリソースを割り当て解除します。デフォルトではこのタスクはブロックを行いますが、noblockが1ならブロックを行いません。
例
insertdeallocatetask(newts,forkkey);
insertproxytask (obj tasksequence, num executerkey, num type [, num/obj involved1, num/obj involved2 , num var1, num var2, num var3, num var4])
プロキシタスクを、調整されたタスクシーケンスに挿入する
説明
プロキシタスクを、指定の調整されたタスクシーケンスに挿入します。
例
insertproxytask(newts, dispatchkey, TASKTYPE_TRAVEL, current.centerObjects[1], NULL,0,0,0,0);
insertsynctask (obj tasksequence, num taskkey)
同期タスクを、調整されたタスクシーケンスに挿入する
説明
同期タスクを、調整されたタスクシーケンスの指定されたタスクに挿入します。
例
insertsynctask(newts, travelkey);
inserttask (obj tasksequence, num type [, obj involved1, obj involved2 , num var1, num var2, num var3, num var4] )
新規タスクをタスクシーケンスに挿入する
説明
このコマンドは廃止されました。代わりにTaskSequence.addTask()を使用してください。指定されたtypeの指定されたtasksequenceに、タスクを挿入します。他のパラメータは、タスクタイプに応じて意味が異なります。各タスクタイプに対応するパラメータの説明については、ユーザーマニュアルの「タスクタイプクイックリファレンス」ガイドを参照してください。
例
inserttask(ts, TASKTYPE_TRAVEL, current, NULL);
movetasksequence (obj tasksequence, obj dispatcher)
ディスパッチャーのタスクシーケンスキューにタスクシーケンスを移動する
説明
このコマンドは廃止されました。代わりにTaskSequence.move()を使用してください。指定されたdispatcherのタスクシーケンスキューに、指定のtasksequenceを移動します。
警告:TaskExecuterによって既に実行中のタスクシーケンスには、このコマンドを絶対に呼び出してはいけません。
警告:TaskExecuterによって既に実行中のタスクシーケンスには、このコマンドを絶対に呼び出してはいけません。
例
movetasksequence(tasksequence, current.centerObjects[1]);
pickoffsetx (obj station, obj item, obj loadingobject)
説明
このコマンドは、loadingobjectがitemをロードするため、xの中央から移動するxオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int xoffset = pickoffsetx(item.up,item,current);
pickoffsety (obj station, obj item, obj loadingobject)
説明
このコマンドは、loadingobjectがitemをロードするため、yの中央から移動するyオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int yoffset = pickoffsety(item.up,item,current);
pickoffsetz (obj station, obj item, obj loadingobject)
説明
このコマンドは、loadingobjectがitemをロードするため、z基点から移動するzオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int zoffset = pickoffsetz(item.up,item,current);
placeoffsetx (obj station, obj item, obj unloadingobject)
説明
このコマンドは、unloadingobjectがitemをアンロードするため、xの中央から移動するxオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int xoffset = placeoffsetx(current.centerObjects[1],item,current);
placeoffsety (obj station, obj item, obj unloadingobject)
説明
このコマンドは、unloadingobjectがitemをアンロードするため、yの中央から移動するyオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int yoffset = placeoffsety(current.centerObjects[1],item,current);
placeoffsetz (obj station, obj item, obj unloadingobject)
説明
このコマンドは、unloadingobjectがitemをアンロードするため、z基点から移動するzオフセットを、stationに照会します。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
オフセット移動の詳細については、TaskExecuterのドキュメントを参照してください。
例
int zoffset = placeoffsetz(current.centerObjects[1],item,current);
profiletasksequence (node tasksequence)
タスクシーケンスの情報を出力コンソールに表示する
説明
tasksequenceの情報を出力コンソールに表示します。
書き込みを行う出力コンソールは開いている必要があります。
出力コンソールを開くには、[ビュー]|[出力コンソール]メニューを使用します。
特定のタスクシーケンスの代わりに、TaskExecuterオブジェクトへの参照を渡すこともできます。
これにより、オブジェクトで現在アクティブなタスクシーケンスのプロファイルが行われます。
書き込みを行う出力コンソールは開いている必要があります。
出力コンソールを開くには、[ビュー]|[出力コンソール]メニューを使用します。
特定のタスクシーケンスの代わりに、TaskExecuterオブジェクトへの参照を渡すこともできます。
これにより、オブジェクトで現在アクティブなタスクシーケンスのプロファイルが行われます。
例
profiletasksequence(gettasksequence(so(), 0));
選択されたオブジェクト(so())のアクティブな(0)タスクシーケンスについて、すべてのタスクシーケンス情報を出力コンソールに書き込みます。
選択されたオブジェクト(so())のアクティブな(0)タスクシーケンスについて、すべてのタスクシーケンス情報を出力コンソールに書き込みます。
reordertasks (obj dispatcher)
ディスパッチャーのすべてのタスクシーケンスをキュー方法に従って並べ替える
説明
関連Dispatcher/TaskExecuterのすべてのタスクシーケンスを、キュー方法に従って並べ替えます。
例
reordertasks(c)
requestoperators (obj dispatcher, obj station, obj involved, num nrofops, num priority, num preempting)
説明
指定された数のオペレーターがstationオブジェクトに到着し、リリースされるまで関連オブジェクトの作業を行うことを要求します。後でオペレーターをリリースするとき、関連オブジェクトをfreeoperators()コマンドに渡す必要があります。呼び出されるオペレーターは、ディスパッチャーにより参照されるオブジェクトか、その出力ポートに接続されている必要があります。
オペレーターに送られるタスクシーケンスには、優先度とプリエンプトの値が与えられます。preemptingの値は次のいずれかです。
0 = PREEMPT_NOT
1 = PREEMPT_ONLY
2 = PREEMPT_AND_ABORT_ACTIVE
3 = PREEMPT_AND_ABORT_ALL
呼び出す必要のある各オペレーターについて、stationでstopobject()が呼び出され、次のようなタスクシーケンスがディスパッチャー(またはオペレーター)オブジェクトに送信されます。
1. タスクシーケンスにプリエンプト「ブックマーク」を配置する(TASKTYPE_MILESTONE)
2. ステーションに移動する(TASKTYPE_TRAVEL)
3. ステーションを再開する(TASKTYPE_STOPREQUESTFINISH)
4. ステーションで活用する(TASKTYPE_UTILIZE)
オペレーターに送られるタスクシーケンスには、優先度とプリエンプトの値が与えられます。preemptingの値は次のいずれかです。
0 = PREEMPT_NOT
1 = PREEMPT_ONLY
2 = PREEMPT_AND_ABORT_ACTIVE
3 = PREEMPT_AND_ABORT_ALL
呼び出す必要のある各オペレーターについて、stationでstopobject()が呼び出され、次のようなタスクシーケンスがディスパッチャー(またはオペレーター)オブジェクトに送信されます。
1. タスクシーケンスにプリエンプト「ブックマーク」を配置する(TASKTYPE_MILESTONE)
2. ステーションに移動する(TASKTYPE_TRAVEL)
3. ステーションを再開する(TASKTYPE_STOPREQUESTFINISH)
4. ステーションで活用する(TASKTYPE_UTILIZE)
例
requestoperators(current.centerObjects[1], current, item, 2, 0, PREEMPT_NOT);
currentオブジェクトの最初のセンターポートに接続されているオブジェクトに接続されている2つのオペレーターを、currentオブジェクトに到達してitemの作業を行うように呼び出します。
currentオブジェクトの最初のセンターポートに接続されているオブジェクトに接続されている2つのオペレーターを、currentオブジェクトに到達してitemの作業を行うように呼び出します。
rerankbesttask (obj object)
説明
このコマンドは、ディスパッチャーとして指定されているオブジェクトのタスクシーケンスキューを走査し、優先度の最も高いタスクシーケンスをキューの先頭に配置します。キューの他のタスクシーケンスは並べ替えされません。
例
rerankbesttask(current);
setcollisioncheck (obj taskexecuter, num checkstate [, num checkinterval])
taskexecuterでの衝突チェックの状態と間隔を設定する
説明
taskexecuterでの衝突チェックの状態と間隔を設定します。checkstateが1なら衝突をチェックし、それ以外ならチェックしません。interval > 0なら、指定されたtaskexecuterについて「衝突チェックの間隔」をリセットします。
例
setcollisioncheck(traveler,1,5);
travelerの衝突チェックを5時間単位ごとに開始します。
travelerの衝突チェックを5時間単位ごとに開始します。
setpreempt (obj tasksequence, num newpreempt)
タスクシーケンスのプリエンプト値を設定する
説明
tasksequenceのプリエンプト値をnewpreemptの値に設定します。可能な値は次のとおりです。
PREEMPT_NOT、
PREEMPT_ONLY、
PREEMPT_AND_ABORT_ACTIVE、
PREEMPT_AND_ABORT_ALL
PREEMPT_NOT、
PREEMPT_ONLY、
PREEMPT_AND_ABORT_ACTIVE、
PREEMPT_AND_ABORT_ALL
例
setpreempt(tasksequence, PREEMPT_NOT);
この例は、タスクシーケンスのプリエンプト値を、プリエンプトを行わないように変更します。
この例は、タスクシーケンスのプリエンプト値を、プリエンプトを行わないように変更します。
setpriority (obj tasksequence, num newpriority)
タスクシーケンスの優先度を設定する
説明
タスクシーケンスの優先度の値を、newpriorityの値に設定します。
例
setpriority(myts, 1);
この例は、タスクシーケンスmytsの優先度の値を1に設定します。
この例は、タスクシーケンスmytsの優先度の値を1に設定します。
ツリーアクセス
FlexSimのツリー構造を経由してノードやオブジェクトを参照するコマンド。
library ()
メインツリーのライブラリノードへの参照
説明
このコマンドは、メインツリーのライブラリノードへの参照を返します。ライブラリを参照する高速な方法として使用されます。
例
treenode SourceObj = library().find("?Source");
変数SourceObjを、ライブラリ内のSourceという名前のノードを参照するよう設定します。
変数SourceObjを、ライブラリ内のSourceという名前のノードを参照するよう設定します。
maintree ()
メインツリーへの参照
説明
メインツリーへの参照を返します。メインツリー内のノードへの文字列パスを定義するとき、次の例に示すようにMAINを使用できます:node("MAIN:/project/exec/globals/cppfunctions");
例
maintree().find("project/exec/globals/cppfunctions");
model ()
モデルのルートノードへの参照
説明
このコマンドは、メインツリー内のモデルノードへの参照を返します。モデルを参照する高速な方法として使用されます。
例
treenode SourceObj = Model.find("Source1");
変数SourceObjを、モデル内のSource1という名前のノードを参照するよう設定します。
変数SourceObjを、モデル内のSource1という名前のノードを参照するよう設定します。
views ()
ビューツリーへの参照
説明
このコマンドは、ビューツリーへの参照を返します。ビューツリーには、現在開いているウィンドウ、および利用可能なGUIについてのすべての情報が含まれています。ビューツリー内のノードへの文字列パスを定義するとき、次の例に示すようにVIEWを使用できます:node("VIEW:/standardviews/ortho");
例
activateview(views().find("standardviews/runcontrol"));
ビューツリーの「standardviews」という名前のノードに格納されている、「runcontrol」という名前のGUIをアクティブにします。
ビューツリーの「standardviews」という名前のノードに格納されている、「runcontrol」という名前のGUIをアクティブにします。
ツリーノードのデータ
ツリーのノードにアクセスおよびデータを割り当てるコマンド。オブジェクトもツリーのノードなので、これらのコマンドの多くはオブジェクトにも使用できます。
$iter (num index)
[ユーザーマニュアル] > [その他の概念] > [SQLクエリ]を参照してください。
説明
詳細については、「その他の概念」 > 「SQLクエリ」を参照してください。
例
checkdllconnection (node dllnode, num force)
ノードがdll関数と正しく接続されていれば、1を返す
説明
ノードがdll関数と正しく接続されていれば、1を返します。それ以外の場合は0を返します。forceが1なら、ノードが接続されていない場合はdll関数へのバインドを試み、成功すれば1を、失敗すれば0を返します。ノードはDLLに切り替えられており、dllへのパスと関数名を指定する正しいデータが存在する必要があります。
例
if(!checkdllconnection(getvarnode(current, "exittrigger"), 1)) msg("DLL Error","Error connecting to dll.")
オブジェクトのexit triggerノードとdll関数との接続を試み、失敗した場合はメッセージを表示します。
オブジェクトのexit triggerノードとdll関数との接続を試み、失敗した場合はメッセージを表示します。
comparetrees (obj tree1, obj tree2)
説明
開発者向けです。ツリーが同一かどうかテストします。
例
comparetrees(node("MAIN:/project/model/1"),node("MAIN:/project/model/2"))
createcoupling (node container1, node container2)
2つのコンテナノード内にポインター結合を作成する
説明
2つのコンテナノード内にポインター結合を作成します。
例
createcoupling(current.labels["items"], item.labels["owner"]);
enablecode (node codenode [, num mode])
ノードをflexscriptまたはC++に切り替える
説明
グローバル設定に基づいて、ノードをflexscriptまたはc++に切り替えます。modeが0なら、グローバル設定を使用してflexscriptまたはc++に切り替えます。ノードが既にflexscriptまたはc++に切り替えられており、modeが0なら、ノードには何も行われません。modeが0以外なら、次のように強制的な切り替えが行われます:1-flexscript、2-c++、3-dll。
このコマンドは、コード編集ウィンドウでノードをflexscript、c++、またはdllに切り替えるため使用されます。
このコマンドは、コード編集ウィンドウでノードをflexscript、c++、またはdllに切り替えるため使用されます。
例
enablecode(var_s(current, "exittrigger"));
findownerobject (node thenode)
説明
このコマンドはownerobject()と同様に、thenodeを含むオブジェクトノードを返します。ownerobject()とは異なり、結果をキャッシュせず、ツリーで「所有者」ノードを検索します。たとえば、TaskExecuterがネットワークパス上でネットワークノードから別のネットワークノードに転送されたとき、TaskExecuterの現在のノードを把握するため、結合ノードは新しいノードに転送され、正しい「所有者」ノードにアクセスするためfindownerobject()が使用されます。
例
findownerobject(c)
getsdtvalue (node sdtNode, str valName)
開発者向け
説明
主に開発者専用です。「SimpleDataType」データを持つノードの名前付きクラスメンバーの値を返します。前方互換性を失う危険があるため、モデルコードでこのコマンドを使用することはお勧めしません。将来のバージョンではクラスメンバーとその名前が再定義される可能性があるため、これらの値に名前でアクセスするモデルコードは将来のバージョンで動作しない可能性があります。
例
nodebreak (node a)
説明
開発者向けです。ノード上で、他のノードを指す結合データを持つ結合ポインターを中断します。ノードが双方向結合の一部である場合、他の結合は影響を受けません。
例
nodebreak(so())
nodeinsertafter (node targetnode)
targetnodeの直後に新規ノードを作成する
説明
このコマンドは、ツリー内のtargetnodeの直後に新規ノードを作成します。新規ノードにはデータは追加されません。データはnodeadddata()コマンドを使用して追加します。ツリー内のどのノードも、targetnodeとして渡すことができます。
例
nodeinsertafter(item.find(">labels").last).dataType = DATATYPE_NUMBER;
itemで参照されるオブジェクトに、数値データを保持する新規ラベルを作成します。
itemで参照されるオブジェクトに、数値データを保持する新規ラベルを作成します。
nodeinsertinto (node containernode)
nodejoin (node a, node b)
説明
開発者向けです。2つのポインターノードを結合して双方向結合を形成します。FlexSimの双方向結合は、データがお互いを指すノードのペアです。FlexSimでは結合が自動的に管理されます。終点のいずれかが削除または無効化された場合、FlexSimはポインターのぶら下がりを防止するためクリーンアップを行います。2つのノードaとbには結合データが必要です。
例
nodejoin(so(),so().next)
objectexists (obj object)
オブジェクトが存在するかどうかチェックする
説明
ドット構文を使用してオブジェクトが存在するかどうかテストする場合、objectexistsを省くことができます。たとえば、if (current.labels["MyLabel"])やif (current.next)の形式を使用できます。
このコマンドは、objectで指定されたオブジェクトがツリーに存在する場合に真(1)を返します。オブジェクトが存在しない場合、偽(0)を返します。
このコマンドは、objectで指定されたオブジェクトがツリーに存在する場合に真(1)を返します。オブジェクトが存在しない場合、偽(0)を返します。
例
if (objectexists(next(current)))
{
moveobject(item, next(current), 1);
}
ツリーのcurrentの後にオブジェクトが存在するかどうかをチェックします。存在するなら、itemで参照されるオブジェクトが、ポート番号1を経由してその中に移動されます。
{
moveobject(item, next(current), 1);
}
ツリーのcurrentの後にオブジェクトが存在するかどうかをチェックします。存在するなら、itemで参照されるオブジェクトが、ポート番号1を経由してその中に移動されます。
ownerobject (node thenode)
実行ノードを「所有」しているオブジェクト(通常は現在のオブジェクト)を取得する
説明
このコマンドは、thenodeが属するサブツリーの先頭であるオブジェクトデータがアタッチされているノードを返します。言い換えると、thenodeを含むオブジェクトノードを返します。このコマンドの結果はthenodeにキャッシュされるため、以後にownerobject(thenode)を呼び出したときはツリーの検索は行われず、キャッシュした結果が返されます。それ以後にthenodeの親が変更された場合も、ownerobject(thenode)はキャッシュした結果を返します。
このコマンドはほとんどのコードフィールドとトリガーフィールドで、アクセス変数currentを設定するため使用されます。これらのフィールドのうち、cはコードを含むノードを参照し、ownerobject(c)はそのノードを「所有」しているオブジェクトを参照します。
このコマンドはほとんどのコードフィールドとトリガーフィールドで、アクセス変数currentを設定するため使用されます。これらのフィールドのうち、cはコードを含むノードを参照し、ownerobject(c)はそのノードを「所有」しているオブジェクトを参照します。

例
string objname = ownerobject(c).name;
objnameを、cで参照されるノードを含むオブジェクトの名前に設定します。cは通常、コードが書き込まれるノードを指します。
treenode current = ownerobject(c);
この例はFlexSimのほとんどのコードフィールドに存在し、「current」オブジェクトへのアクセスを取得します。
objnameを、cで参照されるノードを含むオブジェクトの名前に設定します。cは通常、コードが書き込まれるノードを指します。
treenode current = ownerobject(c);
この例はFlexSimのほとんどのコードフィールドに存在し、「current」オブジェクトへのアクセスを取得します。
removeallcouplingreferences (node thenode)
ツリー内でノードからサブノードへ再帰的に結合を中断する
説明
ツリー内でノードからサブノードへ再帰的に結合を中断します。
例
removeallcouplingreferences(current);
setsdtvalue (node sdtNode, str valName, num/str/node toVal)
開発者向け
説明
主に開発者専用です。「SimpleDataType」データを持つノードの名前付きクラスメンバーの値を設定します。前方互換性を失う危険があるため、モデルコードでこのコマンドを使用することはお勧めしません。将来のバージョンではクラスメンバーとその名前が再定義される可能性があるため、これらの値に名前でアクセスするモデルコードは将来のバージョンで動作しない可能性があります。
例
swapnoderanks (obj/node parentnode, num index1, num index2)
親ノードのサブツリーに含まれる2つのノードのランクを交換する
説明
このコマンドは、親ノードのサブツリーに含まれる2つのノードのランクを交換します。ランクの交換は、特にノードのリストが非常に大きい場合、setrank()を使用するより高速です。
例
swapnoderanks(parentNode,4,parentNode.subnodes.length);
parentNodeのサブツリーに含まれるランク4のノードと、parentNodeのサブツリーに含まれる最後のノードとを交換します。これにより、リストが非常に大きい場合に、parentNodeのサブツリーからノードを高速で削除できます。このコマンドでは最後のノードが4番目の位置に置かれるため、ツリー内での順序が問題にならない場合のみ使用できることに注意してください。言い換えると、これによってfifoの順序が破壊されます。
parentNodeのサブツリーに含まれるランク4のノードと、parentNodeのサブツリーに含まれる最後のノードとを交換します。これにより、リストが非常に大きい場合に、parentNodeのサブツリーからノードを高速で削除できます。このコマンドでは最後のノードが4番目の位置に置かれるため、ツリー内での順序が問題にならない場合のみ使用できることに注意してください。言い換えると、これによってfifoの順序が破壊されます。
switch_cppfunc (node thenode[, num off/on])
thenodeの「C++」フラグを取得または設定する
説明
thenodeの「C++」フラグを取得または設定します。値が1ならC++、0ならC++以外、-1なら現在の値を取得します。ノードがC++に切り替えられると、コンパイル時にC++関数としてコンパイルされます。
例
switch_cppfunc(so(),1)
switch_destroyonreset (obj thenode[, num off/on])
オブジェクトの「リセット時に破棄」フラグを取得または設定する
説明
ノードの「リセット時に破棄」フラグを取得または設定します。フラグが1なら、モデルがリセットされるときノードが削除されます。off/onの値が0または1ならフラグを設定し、-1なら現在の値を取得します。
例
switch_destroyonreset(so(),1)
switch_dllfunc (node dllnode[, num on/off/get])
説明
ノードのdllトグルをオンまたはオフに切り替えます。1ならオンに、0ならオフに切り替え、-1なら現在の状態を取得します。
例
switch_dllfunc(getvarnode(current, "exittrigger"), 1);
switch_expanded (node thenode[, num off/on])
thenodeのサブレベルノードを展開/折りたたみする
説明
ツリービューのthenodeのサブレベルノードを展開または折りたたみします。これは、ツリービューのthenodeの+および-記号をクリックするのと同様の操作です。値が1なら展開、0なら折りたたみ、-1なら現在の値を取得します。
例
switch_expanded(so(),1)
switch_flexscript (obj object[, num on/off/query])
説明
開発者向けです。このコマンドは、ノードのflexscriptトグルを切り替えます。
0 = ノードをflexscript以外に切り替える
1 = ノードをflexscriptに切り替える
-1 = ノードが切り替えられているか(1)いないか(0)を照会する
0 = ノードをflexscript以外に切り替える
1 = ノードをflexscriptに切り替える
-1 = ノードが切り替えられているか(1)いないか(0)を照会する
例
switch_flexscript(var_s(current, "code"), 1);
switch_hashedlist (obj thenode[, num off/on])
thenodeの「ハッシュリスト」フラグを取得または設定する
説明
thenodeの「ハッシュリスト」フラグを取得または設定します。値が1なら、ノードのサブノードを名前で高速にルックアップするため、ハッシュリストをノードに格納するよう設定します。値が0なら、サブノードのハッシュリストをノードに格納しないよう設定します。値が-1なら、現在の値を取得します。
例
switch_hashedlist(so(),1)
switch_noselect (obj object[, num off/on])
オブジェクトの「選択なし」フラグを取得または設定する
説明
ノードオブジェクトの「選択なし」(オブジェクトノードが保護されていることを示すため、ツリービューで灰色に強調表示される)フラグを取得または設定します。値が1なら選択不能に、0なら選択可能に設定し、-1なら現在の値を取得します。オブジェクトを選択なしに設定すると、そのオブジェクトは3Dビューでマウスによりクリックできなくなります。
例
switch_noselect(so(),1)
switch_orphancoupling (obj thenode[, num off/on])
オブジェクトの「孤立結合」フラグを取得または設定する
説明
ノードの「孤立結合」フラグを取得または設定します。フラグが1なら、結合ノードがコピーされるとき、コピーが有効なノードを指さなくなっても破棄されません。off/onの値が0または1ならフラグを設定し、-1なら現在の値を取得します。
例
switch_orphancoupling(so(),1)
switch_preservecoupling (obj thenode[, num off/on])
オブジェクトの「結合保持」フラグを取得または設定する
説明
ノードの「結合保持」フラグを取得または設定します。フラグが1なら、結合ノードがコピーされるとき、コピーもそのノードのパートナーを指します。一方向結合の場合、オリジナルとコピーの両方が同じパートナーノードを指すことになります。双方向結合の場合、新しいパートナーノードが作成されます。off/onの値が0または1ならフラグを設定し、-1なら現在の値を取得します。
例
switch_preservecoupling(so(),1)
switch_protected (obj object[, num off/on])
オブジェクトの「保護済み」フラグを取得または設定する
説明
ノードオブジェクトの「保護済み」(オブジェクトノードが保護されていることを示すため、ツリービューで灰色に強調表示される)フラグを取得または設定します。値が1なら保護済みに、0なら保護なしに設定し、-1なら現在の値を取得します。オブジェクトを保護すると、マウスで移動、回転、サイズ変更できなくなりますが、ダブルクリックしてオブジェクトの[パラメータ]ウィンドウにアクセスすることはできます。ビューウィンドウにはviewignoreobjectsという名前の属性があり、ビュー内のすべてのオブジェクトを無視するため使用できます。この場合、ダブルクリックも含めてどのような方法でも、マウスでオブジェクトを操作できなくなります。
例
switch_protected(so(),1)
switch_selected (obj thenode[, num off/on])
thenodeの「選択済み」フラグを取得または設定する
説明
thenodeの「選択済み」フラグ(赤色の強調表示)を取得または設定します。値が1なら選択済み、0なら未選択、-1なら現在の値を取得します。
例
switch_selected(so(),1)
switch_statelocked (obj object[, num off/on])
説明
ノードオブジェクトの「コード状態ロック」フラグを取得または設定します。値が1ならロックを有効に、0なら無効に設定し、-1なら現在の値を取得します。ロックが有効な場合、そのノードはC++またはflexscriptのうち、現在有効な方にロックされ、メインメニューで[すべてのコードをC++/Flexscriptにする]を選択してもモデルは変更されません。
例
switch_statelocked(so(),1)
switch_stateused (obj thenode[, num off/on])
説明
開発者向けです。状態プロファイル内のノードがどこでオブジェクトにより使用されるかを取得または設定します。このフラグはsetstate()コマンドにより自動的に設定されるため、開発者はUI開発の目的で、オブジェクトにより使用されている状態を知ることができます。
例
switch_stateused(so(),1)
ユーザーインターフェイス
メニュー、ツールバー、ビュー、編集ウィンドウなどのユーザーインターフェイスの実装や管理に関連するコマンド。
activateview (obj viewnode)
説明
開発者向けです。このコマンドは、GUIウィンドウをアクティブにし、画面に表示します。ビューツリー内に格納されているウィンドウを、アクティブツリー内にビューのコピーを作成せずに開くには、このコマンドを使用します。これにより行われた直接的な変更は、ウィンドウを閉じた時に削除されず、ビューツリーに保存されます。通常、GUIウィンドウを開くにはcreateview()コマンドを使用します。既に開いているビューをアクティブ(上端の)ウィンドウにするにはmakeactive()を使用します。
例
activateview(views.find("standardviews/other/FindReplace"));
ビューツリー内のstandardviews/otherというフォルダに、FindReplaceという名前のノードを開きます。
ビューツリー内のstandardviews/otherというフォルダに、FindReplaceという名前のノードを開きます。
activedocumentnode ()
現在アクティブなドキュメントウィンドウを取得する
説明
現在アクティブなドキュメントウィンドウを返します。アクティブなドキュメントウィンドウがタブ付きウィンドウの場合、アクティブなタブページのノードを返します。
例
treenode activedoc = activedocumentnode();
activedocumentview ()
現在アクティブなドキュメントウィンドウをHWNDとして取得する
説明
現在アクティブなドキュメントウィンドウをHWNDとして返します。ウィンドウに関連付けられているノードを取得するには、activedocumentnode()を使用します。
例
treenode activedoc = nodefromwindow(activedocumentview());
activeview ()
現在アクティブなウィンドウをHWNDとして取得する
説明
現在アクティブなウィンドウをHWNDとして返します。ウィンドウに関連付けられているノードを取得するには、nodefromwindow()を使用します。
例
treenode viewnode = nodefromwindow(activeview());
addviewtext (node view, string text)
説明
開発者向けです。指定されたウィンドウにテキストを追加します。
例
addviewtext(sv(),"Hello")
applicationcommand (str name[, p1, p2, p3, ...])
説明
開発者向けです。名前で指定されたコマンドを実行します。このコマンドは、VIEW:/nodefunctions、MAIN:/project/exec/globals/nodefunctions、VIEW:/commands、最後にFlexSimエンジンの順で名前付きノードを検索します。切り替え済みノードが見つかった場合、そのノードのnodefunctionを呼び出し、最大10の数値パラメータを渡します。切り替えられていないノードが見つかった場合、そのノードのexecutefsnode()を呼び出し、n1をc、n2をi、n3をeventcodeとして渡します。
例
applicationcommand("outputconsole");
applyalleditstonodes ([obj view])
説明
開発者向けです。すべてのビュー編集を適用します。この動作はコンパイルまたは保存の前に行われます。
例
applyalleditstonodes
applyeditstonode (obj view, obj editednode)
説明
開発者向けです。ノードにビュー変更を適用します。この動作は通常はテーブルビューでのみ必要なもので、テーブルの現在アクティブなセル以外の場所をクリックするのと本質的に同じです。このコマンドはapplytoeditsの逆の動作を行います。
例
applyeditstonode(ownerview(c), current)
applylinks (node view [, num refresh])
説明
開発者向けです。このコマンドは、viewで指定されたビューウィンドウのすべてのホットリンクとコールドリンクを適用します。refreshが1ならリンクが更新され、モデルからの値が取得されてウィンドウコントロール自体に設定されます。refreshが0なら、モデルの値はユーザーがビューで指定した内容に従って設定されます。このコマンドは、Flexscript GUIのプログラミングで使用されます。
例
applylinks(ownerview(c));
選択されたビューとして現在割り当てられているウィンドウの、すべてのリンクを適用します。
選択されたビューとして現在割り当てられているウィンドウの、すべてのリンクを適用します。
applytoedits (obj view, obj editednode)
説明
開発者向けです。ノードがビューで選択されていれば、そのノードにプログラムによる変更を適用します。このコマンドは通常、テーブルビューでのみ必要になります。このコマンドはapplyeditstonode()の逆の動作を行います。
例
applytoedits(ownerview(c), current)
attlink (node viewdatanode, str path)
説明
開発者向けです。ビューのobjectfocusに相対的なテキストパスでノードを検索します。このコマンドは、viewdatanodeのownerviewのオブジェクトフォーカスに対する相対パスにあるノードを返します。たとえば、viewdatanodeがOnPressイベントノードなど、ビューの構造内にあるノードとします。さらに、親ビューのobjectfocusがモデル内の「Processor」というオブジェクトを指しているとします。そして、attlink()のpath引数に渡されるのはProcessorオブジェクトの相対パスです。このため、attlinkの呼び出しでpathに「>variables」が渡されたなら、attlinkはProcessorの「variables」へのポインターを返します。そのノードが存在しない場合、attlinkはnullの「safenode」を返します。これは、要求されたノードが見つからなかったことを示しています。戻り値が有効かどうかは、objectexists()コマンドでテストできます。
例
attlink(so(),">variables") // so()はビュー内のデータノード
beginaggregatedundo (obj view, str description)
説明
指定されたビューについて、集計された元に戻すレコードを開始します。このコマンドが実行されてから、次にendaggregatedundo()コマンドまでに実行された、元に戻せるコマンドはすべて、単一の元に戻せる操作としてカプセル化されます。作成されたレコードのidを返します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
int id = beginaggregatedundo(c.find("@/TheTable"),"Name Change");
beginignoreundo ()
説明
beginaggregatedundo()およびendaggregatedundo()と組み合わせて使用します。beginignoreundo()とendignoreundo()の間に呼び出されたコマンドは、集計された元に戻すレコードに、元に戻せるコマンドとして追加されません。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
beginignoreundo();
callwebscriptmethod (obj view, str domid, str methodname, int type [, num/str data ...])
説明
HTMLビューのHTMLドキュメントに含まれるDOM要素のメソッドを呼び出します。メソッドに渡すパラメータのデータタイプを定義する必要があります。次のタイプを使用できます。
CWSM_DOUBLE
CWSM_STRING
CWSM_NODE
CWSM_BUNDLE
CWSM_BUNDLE_HEADER
CWSM_BUNDLE_DATA
CWSM_JSON
メソッドに渡す最後のパラメータはCWSM_ENDの必要があります。
CWSM_JSONタイプを使用する場合、json文字列は「json:」で始まる必要があります。たとえば、「json:{"title":"My Title"}」のようにします。
CWSM_DOUBLE
CWSM_STRING
CWSM_NODE
CWSM_BUNDLE
CWSM_BUNDLE_HEADER
CWSM_BUNDLE_DATA
CWSM_JSON
メソッドに渡す最後のパラメータはCWSM_ENDの必要があります。
CWSM_JSONタイプを使用する場合、json文字列は「json:」で始まる必要があります。たとえば、「json:{"title":"My Title"}」のようにします。
例
callwebscriptmethod(view, "chart", "updateData", CWSM_DOUBLE, time(), CWSM_NODE, getvarnode(current, "data"), CWSM_STRING, "My Title", CWSM_END);
この例は、id「chart」を持つ要素のupdateDataというメソッドを呼び出します。
この例は、id「chart」を持つ要素のupdateDataというメソッドを呼び出します。
checkforexistingview (obj view [, num mode])
説明
開発者向けです。このウィンドウと一致する、現在アクティブなウィンドウが存在するかどうかをチェックします。
アクティブなビューノード内にある各ウィンドウの名前の先頭を、指定されたビューの名前の先頭と比較します。
名前の先頭とともに、それぞれのobjectfocusも比較します。
modeが指定され、0以外の場合、objectfocusの代わりにviewfocusを比較します。
アクティブなビューノード内にある各ウィンドウの名前の先頭を、指定されたビューの名前の先頭と比較します。
名前の先頭とともに、それぞれのobjectfocusも比較します。
modeが指定され、0以外の場合、objectfocusの代わりにviewfocusを比較します。
例
checkforexistingview(c)
clearundohistory ([obj view])
説明
指定されたビューの元に戻す履歴にある、すべての元に戻すレコードを削除します。ビューが指定されない場合、3Dおよびツリーウィンドウで使用されるグローバルな元に戻す履歴がクリアされます。
例
clearundohistory(view);
clickcode ()
説明
開発者向けです。ビューのクリックのタイプを返します。OnClickイベントで使用されます。
DOUBLE_CLICKは1を返します。
LEFT_PRESSは2を返します。
LEFT_RELEASEは3を返します。
RIGHT_PRESSは4を返します。
RIGHT_RELEASEは5を返します。
DOUBLE_CLICKは1を返します。
LEFT_PRESSは2を返します。
LEFT_RELEASEは3を返します。
RIGHT_PRESSは4を返します。
RIGHT_RELEASEは5を返します。
例
if(clickcode()==2)
{
pt("Clicked!!");pr();
}
マウスの左ボタンが押されたとき、出力コンソールに「Clicked!!」という文を表示します。
{
pt("Clicked!!");pr();
}
マウスの左ボタンが押されたとき、出力コンソールに「Clicked!!」という文を表示します。
closeview (node viewnode)
説明
開発者向けです。このコマンドは、viewnodeに指定されたビューを閉じます。viewnodeがビューウィンドウやGUIでない場合、このコマンドは何もしません。ただし、ビューはアクティブなビューのフォルダから削除されません。削除するにはdestroyobject()を使用します。
例
treenode activewindows = views().find("active");
while (activewindows.subnodes.length != 0)
{
closeview(activewindows.first);
}
ビューツリーのアクティブノード内にあるすべてのウィンドウを閉じます。通常はこれで、現在開いているすべてのウィンドウが閉じます。
while (activewindows.subnodes.length != 0)
{
closeview(activewindows.first);
}
ビューツリーのアクティブノード内にあるすべてのウィンドウを閉じます。通常はこれで、現在開いているすべてのウィンドウが閉じます。
codetotemplate (obj code, obj edit)
説明
開発者向けです。
C++/Flexscriptコードをテンプレートコードに変換し、編集のビューテキストをテンプレートコードに設定します。codeパラメータは、C++/Flexscriptコードのテキストを含むノードを参照します。ピックリストのテンプレートコードのドロップダウンで、実際のC++/Flexscriptコードからテンプレートコードを作成するために使用されます。
C++/Flexscriptコードをテンプレートコードに変換し、編集のビューテキストをテンプレートコードに設定します。codeパラメータは、C++/Flexscriptコードのテキストを含むノードを参照します。ピックリストのテンプレートコードのドロップダウンで、実際のC++/Flexscriptコードからテンプレートコードを作成するために使用されます。
例
codetotemplate(so(),sv())
codetotemplatetext (node codeobject, node toobjecttext [, num firstcommentonly])
説明
開発者向けです。C++/Flexscriptコードをテンプレートコードに変換します。toobjecttextのテキストを、codeobjectのテキストにあるコードのテンプレートコードに設定します。
例
combocurrentnode (obj combonode)
説明
開発者向けです。指定されたピックリストのコンボボックスの現在のノードを返します。
例
createview(
"VIEW:/standardviews/picklisttemplate","",
combocurrentnode(c.find("../pickoptions").getPath(0, 1)
);
"VIEW:/standardviews/picklisttemplate","",
combocurrentnode(c.find("../pickoptions").getPath(0, 1)
);
comborefresh (obj combonode)
説明
開発者向けです。ピックリストのコンボボックスのコンテンツを更新します。
例
comborefresh(current);
controlpressed ()
説明
開発者向けです。CTRLキーが押されているかどうかをテストします。
例
controlpressed()
createpopup (str viewpath, str objectfocus, str viewfocus, obj relativeto, num x, num y, num sx, num sy)
新しいポップアップウィンドウを作成する
説明
createviewコマンドと同様に新しいウィンドウを作成します。ただし、このウィンドウはFlexSimが管理し、ユーザーがウィンドウの外側をクリックすると、ウィンドウが閉じられます。コードテンプレートのポップアップは、このコマンドを使用して、テンプレートコードを編集するためのドロップダウンを作成します。ポップアップビューにはスタイル属性が含まれ、WS_POPUPスタイルが指定される必要があります。またビューノードは、ポップアップが設定される場所(通常は、コードの作成に使用するビュー)に対して「相対的に」指定します。また、オフセット場所をrelativetoの左上隅からピクセル単位で指定し、ポップアップのサイズも指定します。
例
treenode combobox = c.find("../pickoptions");
createpopup(
"VIEW:/standardviews/picklisttemplate",
combobox.find(">pickprimary+").getPath(0,1),
combocurrentnode(combobox).getPath(0,1),
combobox,
0,20,combobox.location.x, 150
);
このコードは、FlexSimの編集フィールドの多くでテンプレートコードのポップアップを作成するため使われるのと同様のものです。
createpopup(
"VIEW:/standardviews/picklisttemplate",
combobox.find(">pickprimary+").getPath(0,1),
combocurrentnode(combobox).getPath(0,1),
combobox,
0,20,combobox.location.x, 150
);
このコードは、FlexSimの編集フィールドの多くでテンプレートコードのポップアップを作成するため使われるのと同様のものです。
createundorecord (obj view, obj object, num undocode[, num p1, num p2, num p3])
説明
指定されたビューについて、元に戻すレコードを作成します。作成されたレコードのuniqueidを返します。
元に戻すコードは次のとおりです。
UNDO_AGGREGATED 1
UNDO_MOVE_SIZE_ROTATE 2
UNDO_MOVE_SIZE_ROTATE_GROUP 3
UNDO_SELECTION_CHANGE 4
UNDO_CREATE_OBJECT 5
UNDO_DELETE_OBJECT 6
UNDO_CHANGE_DATA 7
UNDO_CHANGE_RANK 8
UNDO_CHANGE_NAME 9
UNDO_MOVE_OBJECT 10
UNDO_DELETE_COUPLING 11
UNDO_AGGREGATED_FIRST_RECORD 12
UNDO_DESTROY_BRANCH 13
UNDO_CHANGE_FLAGS 14
UNDO_REPLACE_OBJECT 15
UNDO_CUSTOM 16
UNDO_CALLBACK 17
詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
元に戻すコードは次のとおりです。
UNDO_AGGREGATED 1
UNDO_MOVE_SIZE_ROTATE 2
UNDO_MOVE_SIZE_ROTATE_GROUP 3
UNDO_SELECTION_CHANGE 4
UNDO_CREATE_OBJECT 5
UNDO_DELETE_OBJECT 6
UNDO_CHANGE_DATA 7
UNDO_CHANGE_RANK 8
UNDO_CHANGE_NAME 9
UNDO_MOVE_OBJECT 10
UNDO_DELETE_COUPLING 11
UNDO_AGGREGATED_FIRST_RECORD 12
UNDO_DESTROY_BRANCH 13
UNDO_CHANGE_FLAGS 14
UNDO_REPLACE_OBJECT 15
UNDO_CUSTOM 16
UNDO_CALLBACK 17
詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
int id = createundorecord(ownerobject(c), selectedobject(ownerobject(c)), UNDO_CUSTOM);
createview (str viewpath[, str objectfocus, str viewfocus])
説明
開発者向けです。このコマンドは、ビューツリーのアクティブノードに新しいGUIウィンドウを作成します。このウィンドウは、viewpathで与えられたパスを持つウィンドウのコピーです。このウィンドウのオブジェクトフォーカスはobjectfocus、ビューフォーカスはviewfocusに設定されます。ほとんどのGUIウィンドウで、objectfocusとviewfocusは一般に同一です。これらは、そのGUIウィンドウが表すノードのパスです。
例
createview("VIEW:/standardviews/other/FindReplace","MAIN:/project/model/Tools/precision","MAIN:/project/model/Tools/precision");
検索置換のGUIを作成します。
検索置換のGUIを作成します。
cursorinfo (obj/num view, num operation, num x/y/z, num pos/move)
説明
開発者向けです。このコマンドは、多くの機能を1つのコマンドとしてまとめたものです。ウィンドウコントロールを行う目的で、マウスの位置と状態に関する情報を取得するため使用されます。
view:関連付けられているビュー、たとえば正投影や平面ビュー。これはHWNDのこともあります(doubleに格納されます)。
operation:行うオペレーションのタイプ。
1 -平面ビューでカーソルのxまたはy位置を取得します。
2 - 正投影または透視ビューの座標を取得します。
3 - マウスボタンの現在の状態を取得します。
戻り値:
0:ボタンが押されていない
1:左ボタンが押されている
2:右ボタンが押されている
3:左右のボタンが押されている
4:左ボタンがダブルクリックされた
4 - カーソル位置を更新します。
5 - ビューに相対的なカーソルのxまたはy位置を取得します。
6 - 画面座標上のカーソルのxまたはy位置を取得します。
7 - カーソルのxまたはy位置を設定します。
xyz:1(x)、2(y)、3(z)のいずれか。オペレーション3では使用しません。オペレーション4の場合、xyz=1なら、オブジェクトの描画時にカーソル位置が更新されます。xyz=2なら、床の描画時にのみ更新されます。
pos/move:1(pos)または2(move)のいずれかです。1ならマウスの絶対位置が取得され、2なら最後の更新以後の変化が取得されます。オペレーション1~2でのみ使用されます。
この機能の使い方は、自分で色々と試して習熟してください。正投影ビューにOnMouseMove属性を追加してから(追加した後で[構築]|[オブジェクトの属性を再バインドする]を使用してビューの属性を必ず再バインドしてください)、出力コンソールに情報を表示します。
view:関連付けられているビュー、たとえば正投影や平面ビュー。これはHWNDのこともあります(doubleに格納されます)。
operation:行うオペレーションのタイプ。
1 -平面ビューでカーソルのxまたはy位置を取得します。
2 - 正投影または透視ビューの座標を取得します。
3 - マウスボタンの現在の状態を取得します。
戻り値:
0:ボタンが押されていない
1:左ボタンが押されている
2:右ボタンが押されている
3:左右のボタンが押されている
4:左ボタンがダブルクリックされた
4 - カーソル位置を更新します。
5 - ビューに相対的なカーソルのxまたはy位置を取得します。
6 - 画面座標上のカーソルのxまたはy位置を取得します。
7 - カーソルのxまたはy位置を設定します。
xyz:1(x)、2(y)、3(z)のいずれか。オペレーション3では使用しません。オペレーション4の場合、xyz=1なら、オブジェクトの描画時にカーソル位置が更新されます。xyz=2なら、床の描画時にのみ更新されます。
pos/move:1(pos)または2(move)のいずれかです。1ならマウスの絶対位置が取得され、2なら最後の更新以後の変化が取得されます。オペレーション1~2でのみ使用されます。
この機能の使い方は、自分で色々と試して習熟してください。正投影ビューにOnMouseMove属性を追加してから(追加した後で[構築]|[オブジェクトの属性を再バインドする]を使用してビューの属性を必ず再バインドしてください)、出力コンソールに情報を表示します。
例
cursorinfo(c,2,1,1)
deselectall ()
説明
開発者向けです。モデル内のすべてのオブジェクトを選択解除します。
例
deselectall()
distcutoff (num radius)
オブジェクト描画にグローバルに適用されるカットオフ半径を設定する
説明
オブジェクト描画にグローバルに適用されるカットオフ半径(視点から)を設定します。
例
discutoff(10)
distfromviewpoint (obj object, obj view)
ウィンドウビューでオブジェクトが視点からどれだけ離れているか
説明
viewで指定されたビューウィンドウで、objectで指定されたオブジェクトが視点からどれだけ離れているかを返します。この値は、viewが透視投影ウィンドウを参照している場合のみ意味を持ちます。
例
double dist = distfromviewpoint(model().subnodes[2],sv());
distを、視点から、モデル内の最初のオブジェクトまでの距離に設定します。
distを、視点から、モデル内の最初のオブジェクトまでの距離に設定します。
draginfo (num operation[, num val])
マウスのドラッグに関連する値を取得または設定する
説明
マウスのドラッグに関連する値を取得または設定します。
operationは次のいずれかです。
DRAG_INFO_DX 1 - dxを取得する
DRAG_INFO_DY 2 - dyを取得する
DRAG_INFO_DZ 3 - dzを取得する
DRAG_INFO_MDX 4 - mdxを取得する
DRAG_INFO_MDY 5 - mdyを取得する
DRAG_INFO_BUTTON_STATE 6 - ボタンの状態を取得する
DRAG_INFO_SET_DX 7 - dxをvalに設定する
DRAG_INFO_SET_DY 8 - dyをvalに設定する
DRAG_INFO_SET_DZ 9 - dzをvalに設定する
DRAG_INFO_SET_MDX 10 - mdxをvalに設定する
DRAG_INFO_SET_MDY 11 - mdyをvalに設定する
DRAG_INFO_SET_BUTTON_STATE 12 - ボタンの状態をvalに設定する
operationは次のいずれかです。
DRAG_INFO_DX 1 - dxを取得する
DRAG_INFO_DY 2 - dyを取得する
DRAG_INFO_DZ 3 - dzを取得する
DRAG_INFO_MDX 4 - mdxを取得する
DRAG_INFO_MDY 5 - mdyを取得する
DRAG_INFO_BUTTON_STATE 6 - ボタンの状態を取得する
DRAG_INFO_SET_DX 7 - dxをvalに設定する
DRAG_INFO_SET_DY 8 - dyをvalに設定する
DRAG_INFO_SET_DZ 9 - dzをvalに設定する
DRAG_INFO_SET_MDX 10 - mdxをvalに設定する
DRAG_INFO_SET_MDY 11 - mdyをvalに設定する
DRAG_INFO_SET_BUTTON_STATE 12 - ボタンの状態をvalに設定する
例
double dx = draginfo(DRAG_INFO_DX);
dropnodefrom ()
説明
開発者向けです。ノードがドロップされた元のビューを返します。
例
dropnodefrom()
dropnodeto ()
説明
開発者向けです。ノードがドロップされた先のビューを返します。
例
dropnodeto()
dropx ()
ドロップアクションのx位置を取得する
説明
ドロップアクションのx位置を取得します。
例
dropx()
dropy ()
ドロップアクションのy位置を取得する
説明
ドロップアクションのy位置を取得します。
例
dropy()
dropz ()
ドロップアクションのz位置を取得する
説明
ドロップアクションのz位置を取得します。
例
dropz()
endaggregatedundo (obj view, num id)
説明
指定されたビューについて、集計された元に戻すレコードを終了します。このコマンドと、前のbeginaggregatedundo()コマンドの間に実行された、元に戻せるコマンドはすべて、単一の元に戻せる操作としてカプセル化されます。beginaggregatedundo()関数から返されたidを渡します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
endaggregatedundo(c.find("@/TheTable"),id);
endignoreundo ()
説明
beginaggregatedundo()およびendaggregatedundo()と組み合わせて使用します。beginignoreundo()とendignoreundo()の間に呼び出されたコマンドは、集計された元に戻すレコードに、元に戻せるコマンドとして追加されません。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
endignoreundo();
findundorecordbyid (obj view, num id)
説明
指定されたビューについて、指定のidを持つ元に戻すレコードを返します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
int id = createundorecord(ownerobject(c), selectedobject(ownerobject(c)), UNDO_CUSTOM);
treenode record = findundorecordbyid(ownerobject(c),id);
treenode record = findundorecordbyid(ownerobject(c),id);
finishundorecord (obj view, num uniqueid)
説明
指定されたビューについて、元に戻すレコードを終了します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
finishundorecord(view, getundorecordid(record));
getchecked (obj window)
説明
開発者向けです。ボタンのチェック済み状態を返します。
例
getchecked(c)
getcurrentundorecord (obj view)
説明
指定されたビューの元に戻す履歴にある現在の元に戻すレコードと関連付けられている、ツリーノードへのポインターを返します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
treenode record = getcurrentundorecord(view);
getdashboardcontrol (str id [, node startnode])
idと関連付けられているダッシュボードコントロールへの参照を返す
説明
ID値がidであるダッシュボードコントロールへの参照を返します。このコマンドは、IDが一致するコントロールを見つけるまで、開いているすべてのダッシュボードを検索します。startnodeに値を渡すと、startnodeを含むダッシュボードのみが検索されます。ダッシュボードコントロールには、編集フィールド、ボタン、コンボボックスなどが含まれます。
例
treenode accelEdit = getdashboardcontrol("accelEdit", c); //現在のダッシュボードのみを検索する
getfilebrowse (str extension, str extensiondescription[, str defaultreturn, str location, num savemode, node filelist])
標準のWindowsファイルブラウザーダイアログウィンドウを開く
説明
このコマンドは、標準のWindowsファイルブラウザーダイアログウィンドウを開きます。ウィンドウに表示されるファイルの拡張子は、extensionで定義されます。複数の拡張子を指定する場合は、セミコロン(;)で区切ります。descriptionで渡されるテキストは、ファイルブラウザーで開くファイルのタイプの説明として使用されます。このコマンドは、選択されたファイルのパスを文字列として返します。ファイルが選択されていない場合、または[キャンセル]が押された場合、空の文字列を返します。filebrowse()コマンドを参照してください。
例
string shapefile = getfilebrowse("*.3ds; *.wrl","3D shape files");
変数shapefileを、ファイルブラウザーで選択されたファイルのパスに設定します。ブラウには拡張子が.3dsおよび.wrlのファイルが表示されます。
変数shapefileを、ファイルブラウザーで選択されたファイルのパスに設定します。ブラウには拡張子が.3dsおよび.wrlのファイルが表示されます。
getfilesindirectory (str directory, str extension, node destnode)
説明
指定されたディレクトリで、指定の拡張子と一致するすべてのファイルを取得し、一致する各ファイルへのパスを保持しているノードを、destnodeのコンテンツに書き込みます。このコマンドは、見つかった一致ファイルの数を返します。extensionパラメータは、取得するファイルを指定する3文字(場合によっては4文字)の拡張子です。たとえば、.fsmモデルファイルをすべて取得するなら、文字列「fsm」を指定します。また、extensionパラメータに「directories」を渡すと、ディレクトリ内のディレクトリのリストが取得されます。拡張子にかかわらずすべてのファイルを取得するには、extensionパラメータに「*」を渡します。ファイルパスは、destnodeに挿入されるノードの文字列データ(名前ではなく)に設定されます。
例
treenode destnode = Model.find("Tools").subnodes.assert("Files");
int nrfiles = getfilesindirectory(documentsdir(), "*", destnode);
for(int i = 1; i <= nrfiles; i++)
{
mpt("file: ");
mpt(destnode.subnodes[i].value);
mpr();
} getparentwindow (HWND window)
説明
開発者向けです。指定されたウィンドウの親ウィンドウを返します。この関数に渡すパラメータとして、windowfromnodeを使用します。
例
getpickingdrawfocus (obj theview, num whattoget, num pickedid)
ピッキング描画フォーカスを取得する
説明
ピッキング描画フォーカスを取得します。OnClick内で、何がクリックされたのか判定するため使用されます。whattogetパラメータはPICK_TYPE、PICK_OBJECT、PICK_SECONDARY_OBJECTのいずれかです。pickedidは「pressed」ピックではPICK_PRESSED、「hovered」ピックではPICK_HOVERED、「released」ピックではPICK_RELEASED、「mouse moved」ピックではPICK_MOVEDです。
例
int picktype = getpickingdrawfocus(view, PICK_TYPE, 0);
getpickingmode (obj view)
ビューのピッキングモードを取得する
説明
指定されたビューのピッキングモードを取得します。
例
int isselectionmode = getpickingmode(view);
getsystemmetric (num metric[, HWND win])
説明
開発者向けです。システム画面のメトリックを返します。metricに指定する値と、返される値は次のとおりです(特に記載がなければ、値はすべて論理単位です)。
1:デスクトップの幅
2:デスクトップの高さ
3:カーソルの下にあるモニターの作業領域の左端の位置
4:カーソルの下にあるモニターの作業領域の右端の位置
5:カーソルの下にあるモニターの作業領域の上端の位置
6:カーソルの下にあるモニターの作業領域の下端の位置
7:ウィンドウwinのピクセル単位の幅
8:ウィンドウwinのピクセル単位の高さ
9:カーソルの下にあるモニターの左端の位置
10:カーソルの下にあるモニターの右端の位置
11:カーソルの下にあるモニターの上端の位置
12:カーソルの下にあるモニターの下端の位置
13:ウィンドウwinの幅
14:ウィンドウwinの高さ
1:デスクトップの幅
2:デスクトップの高さ
3:カーソルの下にあるモニターの作業領域の左端の位置
4:カーソルの下にあるモニターの作業領域の右端の位置
5:カーソルの下にあるモニターの作業領域の上端の位置
6:カーソルの下にあるモニターの作業領域の下端の位置
7:ウィンドウwinのピクセル単位の幅
8:ウィンドウwinのピクセル単位の高さ
9:カーソルの下にあるモニターの左端の位置
10:カーソルの下にあるモニターの右端の位置
11:カーソルの下にあるモニターの上端の位置
12:カーソルの下にあるモニターの下端の位置
13:ウィンドウwinの幅
14:ウィンドウwinの高さ
例
getsystemmetric(1)
gettableviewselection (obj tableview, num val)
説明
開発者向けです。テーブルビューの青色の選択範囲に基づいて値を返します。valが1なら開始行、2なら開始列、3なら終了行、4なら終了列を返します。
例
int startrow = gettableviewselection(c,1);
getundorecordid (obj record)
説明
指定された元に戻すレコードのidを返します。詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
int id = getundorecordid(getcurrentundorecord(view));
getviewhwnd (obj view, int windowtype)
ビューの特定ウィンドウのHWNDハンドルを取得する
説明
viewの特定ウィンドウのwindows HWNDハンドルを返します。各ビューは、データを正しく表示するため複数のウィンドウを使用することがあります。たとえば、ツリービューにはツリーを表示するメインウィンドウに加えて、ノードの文字列や数値データを編集用に表示するウィンドウや、ノード名を表示/編集するウィンドウが含まれます。windowtypeパラメータは、どのウィンドウハンドルを返すのかを次のように指定します。
1 - メインコントロール(windowfromnode()と同じ)
2 - データコントロール - scintillaコードコントロールで、ツリーおよびスクリプトビュー内のノードのデータを表示する
3 - コントロール - ツリー内で強調表示されたノードの名前を表示/編集するコントロール
4 - ステータスバー - ビューにステータスバーが存在する場合
5 - ツールチップ - ビューのツールチップコントロール
6 - ポインターコントロール - リストのヘッドを表示するツリーでのみ使用
1 - メインコントロール(windowfromnode()と同じ)
2 - データコントロール - scintillaコードコントロールで、ツリーおよびスクリプトビュー内のノードのデータを表示する
3 - コントロール - ツリー内で強調表示されたノードの名前を表示/編集するコントロール
4 - ステータスバー - ビューにステータスバーが存在する場合
5 - ツールチップ - ビューのツールチップコントロール
6 - ポインターコントロール - リストのヘッドを表示するツリーでのみ使用
例
sendwindowmessage(getviewhwnd(treeview,2), SCI_SETSEL, 4, 8);
getviewscale (obj view)
説明
開発者向けです。ビューのスケール係数を返します。
例
getviewscale(sv())
getviewtext (obj/num window)
説明
開発者向けです。ウィンドウのテキストを返します。
例
getviewtext(sv())
highlightviewtext (node view, num pos, num span, num mode span/lines)
コード編集ウィンドウのテキストを強調表示する
説明
scintillaコード編集ウィンドウのテキストを強調表示します。flexscript構文チェッカーで、コード編集ウィンドウの構文エラーを強調表示するために使用されます。行全体でも、個別の文字でも強調表示できます。個別の文字を強調表示するには、modeに2を指定します。行の場合はmodeに1を指定します。行の場合、強調表示の開始行をposに指定し(最初の行が1)、強調表示する行数をspanに指定します。個別の文字の場合、開始位置をposに指定し、強調表示する文字数をspanに指定します(左端の文字が0)。
例
highlightviewtext(c, 0, 5, 2)
scintillaテキスト編集の最初の5文字を強調表示します。
highlightviewtext(c, 1, 1, 1)
scintillaテキスト編集の最初の行を強調表示します。
scintillaテキスト編集の最初の5文字を強調表示します。
highlightviewtext(c, 1, 1, 1)
scintillaテキスト編集の最初の行を強調表示します。
iskeydown ([num key])
説明
開発者向けです。キーボードの指定されたキーが押し下げられている場合、1を返します。最初のパラメータが渡されない場合、いずれかのキーが押し下げられていれば1を返します。そうでない場合、0を返します。
例
iskeydown(74)
keyboardfocus ([HWND/node focus])
キーボードのフォーカスを取得/設定する
説明
GUI開発で使用されます。キーボードのフォーカスを取得/設定します。focusパラメータが指定されない場合、現在のキーボードフォーカスへの参照をHWNDハンドルとして返します。それ以外の場合、キーボードのフォーカスを渡されたパラメータに設定します。ビューノードのHWNDハンドルへのアクセスを取得するには、windowfromnode()またはgetviewhwnd()を使用します。
例
keyboardfocus(windowfromnode(edit));
keyedclick (obj object, num key[, obj view])
説明
開発者向けです。オブジェクトのキー付きクリック機能(X、C、V)を実行します。
例
keyedclick(model().last, 88)
lastclickednode ()
説明
開発者向けです。最後にクリックされたノードへのポインターを返します。
例
lastclickednode()
lastkey ()
説明
開発者向けです。OnKeyPressイベントで押されたキーのキーコードを返します。
例
lastkey()
lastkeydown ()
説明
開発者向けです。OnKeyPressイベントで押されたキーのキーコードを返します。
例
lastkeydown()
lastkeyup ()
説明
開発者向けです。OnKeyPressイベントで押されたキーのキーコードを返します。
例
lastkeyup()
listboxrefresh (obj listbox)
リストボックスのコンテンツを更新する
説明
リストボックスのコンテンツを更新します。
例
listboxrefresh(c.find("../Collision Members"))
makeactive (obj viewwindow)
説明
開発者向けです。指定されたウィンドウをアクティブにします。
例
makeactive(ownerview(c));
msg (str caption, str text [, num buttontype])
メッセージダイアログを表示する
説明
このコマンドはメッセージボックスを作成し、タイトルバーにcaptionを、ボックス内にtextを表示します。メッセージボックスに表示されるボタンは、buttontypeの値に基づきます。[OK]または[はい]が押された場合、msg()は1を返します。[いいえ]が押された場合、msg()は0を返します。[キャンセル]が押されたときに返される値はbuttontypeによって異なります。buttontypeが3なら、[キャンセル]が押されると-1を返し、それ以外の場合は0を返します。buttontypeが指定されない場合は0と見なされます。
buttontypeの値は次のとおりです。
0 - [OK]、[キャンセル]
1 - [OK]
2 - [OK]、[キャンセル]
3 - [はい]、[いいえ]、[キャンセル]
4 - [はい]、[いいえ]
buttontypeの値は次のとおりです。
0 - [OK]、[キャンセル]
1 - [OK]
2 - [OK]、[キャンセル]
3 - [はい]、[いいえ]、[キャンセル]
4 - [はい]、[いいえ]
例
if (msg("Finished", "Close the database?") == 1)
dbclose();
dbclose();
nodefromwindow (num window)
説明
開発者向けです。ウィンドウハンドルのノードを取得します。
例
nodefromwindow(windowfromnode(sv()))
ownerview (obj viewobj)
説明
開発者向けです。ビュー構造の最上位ノードを取得します。
例
ownerview(sv())
pickcolor ()
説明
開発者向けです。カラーピッカーウィンドウを開き、ユーザーが色を選択できるようにします。rbg色コンポーネントの値を取得するには、pickedcolorred()、pickedcolorgreen()、pickedcolorblue()コマンドを使用します。
例
pickcolor();
int bluecomponent = pickedcolorblue();
変数bluecomponentが、pickcolor()で選択された色の青色コンポーネントのrgb値に設定されます。
int bluecomponent = pickedcolorblue();
変数bluecomponentが、pickcolor()で選択された色の青色コンポーネントのrgb値に設定されます。
pickcolornode (obj colornode)
説明
開発者向けです。カラーピッカーウィンドウを開き、オブジェクトの色属性ノードのrgb色値を設定します。
例
pickcolornode(color(current));
カラーピッカーウィンドウを開き、currentオブジェクトの色を選択された色に設定します。
カラーピッカーウィンドウを開き、currentオブジェクトの色を選択された色に設定します。
pickedcolorblue ()
説明
開発者向けです。pickcolor()コマンドで選択された色の青色コンポーネントを返します。
例
pickcolor();
int bluecomponent = pickedcolorblue();
変数bluecomponentが、pickcolor()で選択された色の青色コンポーネントのrgb値に設定されます。
int bluecomponent = pickedcolorblue();
変数bluecomponentが、pickcolor()で選択された色の青色コンポーネントのrgb値に設定されます。
pickedcolorgreen ()
説明
開発者向けです。pickcolor()コマンドで選択された色の緑色コンポーネントを返します。
例
pickcolor();
int greencomponent = pickedcolorgreen();
変数greencomponentが、pickcolor()で選択された色の緑色コンポーネントのrgb値に設定されます。
int greencomponent = pickedcolorgreen();
変数greencomponentが、pickcolor()で選択された色の緑色コンポーネントのrgb値に設定されます。
pickedcolorred ()
説明
開発者向けです。pickcolor()コマンドで選択された色の赤色コンポーネントを返します。
例
pickcolor();
int redcomponent = pickedcolorred();
変数redcomponentが、pickcolor()で選択された色の赤色コンポーネントのrgb値に設定されます。
int redcomponent = pickedcolorred();
変数redcomponentが、pickcolor()で選択された色の赤色コンポーネントのrgb値に設定されます。
pickfile (str extension, str extensiondescription)
説明
開発者向けです。ファイルブラウザーを開き、ユーザーがファイルを選択できるようにします。ブラウザーでは、指定された拡張子のファイルを探します。extensiondescriptionは、許可されるファイルタイプについて説明する任意のテキストです。このコマンドは、選択したファイルのフルパスを返します。filebrowse()コマンドを参照してください。
例
pickfile("*.xls","Excel Workbooks")
picklistapply (obj combobox)
説明
開発者向けです。ピックリストのコンボボックスで選択されたオプションを適用します。この操作はapplylinksが呼び出されたとき、または[OK]や[適用]ボタンが押されたときに行われます。
例
picklistapply(c)
redirectconsole (num console:output/system/compiler/trace, obj view)
与えられたコンソールへの出力をリダイレクトする
説明
与えられたコンソールへの出力を、指定されたビューのビューテキストに出力されるようリダイレクトします。CONSOLE_OUTPUTは出力コンソールを、CONSOLE_SYSTEMはシステムコンソールを、CONSOLE_COMPILERはコンパイラーコンソールを、CONSOLE_TRANCEはトレースコンソールをリダイレクトします。リダイレクトを元のコンソールに戻すには、このコマンドを再度呼び出してviewパラメータにNULLを指定します。
例
redirectconsole(2, c);
buildnodeflexscript(getvarnode(Model.find("Processor1"), "exittrigger"));
redirectconsole(2, NULL);
コンパイラーコンソールをview cにリダイレクトしてから、モデル内のノードのflexscriptを構築します。これにより、flexscript構築時のエラーはコンパイラーコンソールではなくview cに出力されます。
buildnodeflexscript(getvarnode(Model.find("Processor1"), "exittrigger"));
redirectconsole(2, NULL);
コンパイラーコンソールをview cにリダイレクトしてから、モデル内のノードのflexscriptを構築します。これにより、flexscript構築時のエラーはコンパイラーコンソールではなくview cに出力されます。
redirectpicklists (obj view)
説明
開発者向けです。リダイレクトされているパラメータまたはプロパティウィンドウのすべてのピックリストを調整します。
例
redo (obj view)
説明
指定されたビューで以前に元に戻されたアクションをやり直します。指定されたビューには、元に戻せるアクションを記録するundohistory属性が必要です。
例
redo(view);
refreshview (obj view)
説明
開発者向けです。ビューの定義からウィンドウを再生成します。
例
refreshview(c)
repaintall ()
説明
開発者向けです。すべてのウィンドウを再描画します。
例
repaintall()
repaintallactive ()
説明
開発者向けです。アクティブリストのすべてのウィンドウを再描画します。
例
repaintallactive()
repaintview (obj view)
説明
開発者向けです。再生成を行わずにウィンドウを再描画します。
例
repaintview(c)
repositionhighlightededits (obj view)
説明
開発者向けです。ツリービューの強調表示されたオブジェクトの編集コントロールの位置を変更します。
例
scrollinfo (obj/HWND view, num get_set {0-1}, num horz_vert_ctl {0-2}, num scrollinfo {1-4}[, num value])
説明
開発者向けです。viewのスクロールバーのscrollinfoを取得または設定します。valueパラメータは、get_setが1の場合のみ使用されます。スクロールバーの位置(nPos)は、scrollinfo 4により変更されます。スクロールバーのnMin、nMax、nPageの値は、それぞれscrollinfo 1、2、3により取得および設定できます。
例
scrollinfo(TheTable,1,1,4,scrollinfo(c,0,1,4)-amount);
select (obj window)
説明
開発者向けです。指定されたビューオブジェクトを選択します。
例
select(ownerview(c))
selectedobject (obj window [, num reset])
説明
開発者向けです。ビューの強調表示されているノードを取得します。
例
selectedobject(ownerview(c))
selectedx (obj window)
説明
開発者向けです。ビューの強調表示されているオブジェクトのx位置を取得します。
例
selectedx(ownerview(c))
selectedy (obj window)
説明
開発者向けです。ビューの強調表示されているオブジェクトのy位置を取得します。
例
selectedy(ownerview(c))
selectedz (obj window)
説明
開発者向けです。ビューの強調表示されているオブジェクトのz位置を取得します。
例
selectedz(ownerview(c))
sendonactivatenotify ()
説明
開発者向けです。各パレットウィンドウのOnActivateNotifyイベントを起動します。
例
sendonactivatenotify();
setcameradirection (obj view, num x, num y, num z, num rx, num ry, num rz)
3Dビューの視点方向を設定する
説明
正投影または透視投影ビューの視点方向を設定します。(x,y,z)はカメラのフォーカスポイントです。(rx, ry, rz)はカメラの回転です。関連付けられているビュー属性名は、それぞれviewpointx、viewpointy、viewpointradius、viewpointrx、viewpointry、viewpointrzです。
例
setcameradirection(sv(), 0, 0, 0, -40, 0, 25);
setcameravolume (obj view, num w, num h, num nearclip, num farclip, num magnification, num fov, num projtype, num firstperson)
説明
開発者向けです。OpenGLカメラボリュームを設定します。setcameradirectionでは設定されない追加のviewパラメータを設定します。
例
例はありません。
setchecked (obj view, num value)
説明
開発者向けです。ボタンのチェック済み状態を設定します。
例
setchecked(c,0) ;
setcursor (num cursorid)
マウスポインターのビジュアルな外観を設定する
説明
マウスポインターのビジュアルな外観を設定します。有効なidは次のとおりです。
1:Arrow
2:IBeam
3:Wait
4:Cross
5:UpArrow
6:Size
7:Icon
8:SizeNWSE
9:SizeNESW
10:SizeWE
11:SizeNS
12:SizeAll
13:No
14:Hand
15:AppStarting
16:Help
1:Arrow
2:IBeam
3:Wait
4:Cross
5:UpArrow
6:Size
7:Icon
8:SizeNWSE
9:SizeNESW
10:SizeWE
11:SizeNS
12:SizeAll
13:No
14:Hand
15:AppStarting
16:Help
例
setcursor(3)
setdropcoords (obj view[, obj dropnodefrom, obj dropnodeto])
説明
開発者向けです。マウスの現在の位置に基づいて、viewのdropx()およびdropy()座標コマンドを設定します。オプションとして、dropnodefromおよびdropnodetoパラメータを設定し、dropnodefrom()およびdropnodeto()で返されるノードを定義することもできます。
例
setdropcoords()
setpickingdrawfocus (obj theview, obj focus, num what[, obj secondaryfocus, num flags])
説明
開発者向けです。この呼び出しの後でクリックやドラッグを行ったとき、フォーカスとして選択される描画コードを設定します。通常はこのコマンドを使用して、オブジェクトにカスタムのサイズ変更ツールやグリッパを描画してから、オブジェクトにOnDragまたはOnClickイベントを実装して、getpickingdrawfocus()を呼び出し、どの部分がクリックされたのかを特定します。
flagsは「DETECT_DRAG」設定の1つと、オプションの「オーバーライド」ビットをビット単位で組み合わせたものです。オーバーライドビットはフォーカス選択の定義には使用されず、サイズ変更ツールや境界ボックスの通常の描画をオーバーライドするようFlexSimに指示します。
DETECT_DRAG_X、DETECT_DRAG_Y、DETECT_DRAG_Z - 与えられた軸に沿って、描画対象のオブジェクトに相対的なドラッグのみを検出します。OnDragイベント内のdraginfo()コマンドでこのオプションを使用すると、オブジェクトがどこにドラッグされているのかを特定できます。
DETECT_DRAG_XY、DETECT_DRAG_YZ、DETECT_DRAG_XZ - 与えられた平面に沿ったドラッグのみを検出します。これらのオプションも、OnDragイベント内のdraginfo()コマンドで使用します。
OVERRIDE_DRAW_SIZER_X、OVERRIDE_DRAW_SIZER_Y、OVERRIDE_DRAW_SIZER_Z、OVERRIDE_DRAW_SIZER_X_NEG、OVERRIDE_DRAW_SIZER_Y_NEG、OVERRIDE_DRAW_SIZER_Z_NEG、OVERRIDE_DRAW_SIZER_ALL - これらのフラグを使用すると、エンジンはフラグ付きのサイズ変更ツールを描画しません。
OVERRIDE_DRAW_YELLOW_BOX - オブジェクトが選択されたとき、周囲に黄色のボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_GREEN_BOX - オブジェクトの周囲に緑色の「統計アクティブ」ボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_REDBOX - オブジェクトが選択されたとき、周囲に赤色の選択ボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_HOVERBOX - オブジェクトの上にマウスカーソルを移動したとき、周囲に黄色のホバーボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_ALL - オブジェクトの周囲にいかなるサイズ変更ツールやボックスも描画しないようFlexSimに指示します。
OVERRIDE_SET_MOUSE_DOWN_PICK - ビューの「マウスダウン」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスのボタンが押されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_DOWN_PICK - ビューの「マウスアップ」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスのボタンが離されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_MOVE_PICK - ビューの「マウス移動」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスが移動されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_HOVER_PICK - ビューの「マウスホバー」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上にマウスカーソルが移動されたのと同様に選択情報を更新します。
flagsは「DETECT_DRAG」設定の1つと、オプションの「オーバーライド」ビットをビット単位で組み合わせたものです。オーバーライドビットはフォーカス選択の定義には使用されず、サイズ変更ツールや境界ボックスの通常の描画をオーバーライドするようFlexSimに指示します。
DETECT_DRAG_X、DETECT_DRAG_Y、DETECT_DRAG_Z - 与えられた軸に沿って、描画対象のオブジェクトに相対的なドラッグのみを検出します。OnDragイベント内のdraginfo()コマンドでこのオプションを使用すると、オブジェクトがどこにドラッグされているのかを特定できます。
DETECT_DRAG_XY、DETECT_DRAG_YZ、DETECT_DRAG_XZ - 与えられた平面に沿ったドラッグのみを検出します。これらのオプションも、OnDragイベント内のdraginfo()コマンドで使用します。
OVERRIDE_DRAW_SIZER_X、OVERRIDE_DRAW_SIZER_Y、OVERRIDE_DRAW_SIZER_Z、OVERRIDE_DRAW_SIZER_X_NEG、OVERRIDE_DRAW_SIZER_Y_NEG、OVERRIDE_DRAW_SIZER_Z_NEG、OVERRIDE_DRAW_SIZER_ALL - これらのフラグを使用すると、エンジンはフラグ付きのサイズ変更ツールを描画しません。
OVERRIDE_DRAW_YELLOW_BOX - オブジェクトが選択されたとき、周囲に黄色のボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_GREEN_BOX - オブジェクトの周囲に緑色の「統計アクティブ」ボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_REDBOX - オブジェクトが選択されたとき、周囲に赤色の選択ボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_HOVERBOX - オブジェクトの上にマウスカーソルを移動したとき、周囲に黄色のホバーボックスを描画しないようFlexSimに指示します。
OVERRIDE_DRAW_ALL - オブジェクトの周囲にいかなるサイズ変更ツールやボックスも描画しないようFlexSimに指示します。
OVERRIDE_SET_MOUSE_DOWN_PICK - ビューの「マウスダウン」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスのボタンが押されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_DOWN_PICK - ビューの「マウスアップ」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスのボタンが離されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_MOVE_PICK - ビューの「マウス移動」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上でマウスが移動されたのと同様に選択情報を更新します。
OVERRIDE_SET_MOUSE_HOVER_PICK - ビューの「マウスホバー」選択を定義された値に明示的に設定します。これは描画シーケンスの外側で呼び出され、そのオブジェクト上にマウスカーソルが移動されたのと同様に選択情報を更新します。
例
setpickingdrawfocus(view, current, 20, drawsurrogate(current).first.subnodes[3], DETECT_DRAG_Y);
setselectedobject (obj view, obj selected)
説明
開発者向けです。viewのselectedobject(黄色で強調表示されたオブジェクト)を設定します。これはso()とは異なることに注意してください。強調表示されたオブジェクトにはselectedobject()コマンドでアクセスします。
例
setselectedobject(ownerview(c), model().first)
settableviewselection (obj tableview, num startrow, num startcol, num endrow, num endcol[, num rangeselected])
説明
開発者向けです。tableviewに青色の選択範囲を設定します。数値パラメータのいずれかが0より小さい場合、すべてを選択解除します。ヘッダーセルを選択するには0を使用します。
例
settableviewselection(c,0,1,2,2);
setviewtext (obj/HWND window, str text)
説明
開発者向けです。gui編集フィールドのテキストを設定します。
例
setviewtext(c,"hello")
shiftpressed ()
説明
開発者向けです。SHIFTキーが押されているかどうかをテストします。
例
shiftpressed()
showcompilerconsole ()
説明
開発者向けです。コンパイラーコンソールを表示します。
例
showcompilerconsole()
showhelp (str topicname)
説明
開発者向けです。topicnameで指定されたヘルプトピックを開きます。
例
showhelp("getting_started");
showhtmlhelp (str topic)
説明
開発者向けです。FlexSimのユーザーマニュアルで、指定されたtopicを開きます。
例
showhtmlhelp("Welcome_to_Flexsim.html")
standardpreopen (obj object[, int nobuild])
説明
開発者向けです。現在のウィンドウとして開くのと同じウィンドウが既に開いているどうか照会します。開いている場合、現在のウィンドウを閉じます。
例
standardpreopen(c)
sv ()
sv()として割り当てられた最後のビューへの参照を取得する
説明
このコマンドは、選択されたビューを割り当てられた最後のビューウィンドウへの参照を返します。ビューウィンドウを割り当てるには、ウィンドウで何もオブジェクトが描画されていない部分を右クリックし、[(sv)として設定]を選択します。開いているビューウィンドウ(例:正投影やVR)のどれでも、選択されたビューを割り当てられます。
例
flypath(sv(),1);
選択されたビューとして現在割り当てられているビューのフライパス1番を開始します。
選択されたビューとして現在割り当てられているビューのフライパス1番を開始します。
systemwindow (num windowtype)
説明
開発者向けです。システムウィンドウへのHWNDハンドルを取得します:1-出力 2-システム 3-コンパイラー 4-トレース 5-コマンド 6-属性 7-完了 8-アプリ 9-アプリsb 10-出力編集 11-コンパイラー編集 12-トレース編集 13-システム編集
例
systemwindow(1)
tabcontrolrefresh (obj tabcontrolnode)
説明
開発者向けです。タブコントロールを更新します。
例
tabcontrolrefresh(c.find("@/tabcontrol"));
templatetocode (obj code, obj edit)
説明
開発者向けです。テンプレートコードをc++に適用します。このコマンドは、編集済みのテンプレートコードを、それを作成したC++/Flexscriptコードに適用するため、ピックリストのテンプレートコードのドロップダウンで使用されます。
例
templatetocode(so(),sv())
undo (obj view)
説明
指定されたviewについて以前に記録されたアクションを、元に戻します。指定されたビューには、元に戻せるアクションを記録するundohistory属性が必要です。
例
undo(view);
updateundorecord (obj view, num uniqueid[, num updatetype, num p1, num p2])
説明
指定されたviewについて、元に戻すレコードを更新します。
次に示す、元に戻すレコードタイプを更新する必要があります。
UNDO_MOVE_SIZE_ROTATE
UNDO_MOVE_SIZE_ROTATE_GROUP
UNDO_SELECTION_CHANGE
詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
次に示す、元に戻すレコードタイプを更新する必要があります。
UNDO_MOVE_SIZE_ROTATE
UNDO_MOVE_SIZE_ROTATE_GROUP
UNDO_SELECTION_CHANGE
詳細については、「その他の概念」 > 「元に戻す詳細機能」を参照してください。
例
updateundorecord(view, getundorecordid(record));
viewdist (obj view, obj object)
ビューのフォーカスポイントからオブジェクトまでの距離を取得する
説明
ビューのフォーカスポイントからオブジェクトまでの距離を返します。
例
if(viewdist(view, current) > 100) ;
このコマンドは、ビューの視点とcurrentオブジェクトとの間の距離が100より大きいかどうかを照会します。
このコマンドは、ビューの視点とcurrentオブジェクトとの間の距離が100より大きいかどうかを照会します。
webcommand (str name[, p1, p2, p3, ...])
FlexSimのHTMLエンジン/ウィジェットの操作に使用する
説明
FlexSimのHTMLエンジン、htmlウィジェットなどの操作に使用するコマンドです。
例
string innerhtml = webcommand("getelementinnerhtml", view, "title");
windowflash (HWND window, num count, num timeout)
説明
開発者向けです。指定されたウィンドウをフラッシュします。countはウィンドウをフラッシュする回数です。timeoutは、フラッシュの間隔をコントロールします。timeoutが0なら、デフォルトのカーソル点滅速度が使用されます。
例
windowflash(windowfromnode(ownerview(c)),2,125);
windowfromnode (obj viewnode)
説明
開発者向けです。ビューノードのウィンドウハンドル(HWND)を取得します。
例
windowfromnode(c)
windowgray (HWND window, num graystate)
説明
開発者向けです。graystateパラメータ(1または0)に従ってウィンドウを有効または無効にします。
例
graywindow(windowfromnode(c),1);
windowmove (HWND window, num x, num y, num sx, num sy[, num refresh])
説明
開発者向けです。ウィンドウを指定されたx,yピクセルの場所に移動し、サイズをsx,syピクセルに設定します。refreshが1なら、ウィンドウの再描画を行います。
例
windowmove(windowfromnode(c),10,10,200,200,1)
windowshow (HWND/node thewindow , num show)
説明
開発者向けです。ウィンドウを表示/非表示にします。2番目のパラメータが1なら、ウィンドウを表示します。それ以外の場合、ウィンドウを非表示にします。
例
windowshow(windowfromnode(c))
windowstyle (HWND/obj window [, num style, num useexstyle])
ウインドウのウィンドウスタイルを取得する
説明
GUI開発で使用されます。与えられたウィンドウのウィンドウスタイルを動的に取得または設定します。styleが0なら、ウィンドウの現在のスタイルが返されます。それ以外の場合はスタイルを設定します。useexstyleが1なら、ウィンドウの拡張スタイルを適用または取得します。ウィンドウスタイルの詳細については、Windows SDKのドキュメントを参照してください。
例
例として、このコマンドを透視投影ビューの[全画面]コンテキストメニューオプションで使用し、透視投影ウィンドウが全画面モードになったときタイトルバーが表示されないよう、スタイルを変更できます。