［マスフローコンベヤの動作］パネル

［マスフローコンベヤの動作］パネルは、マスフローコンベヤの動作プロパティを定義します。

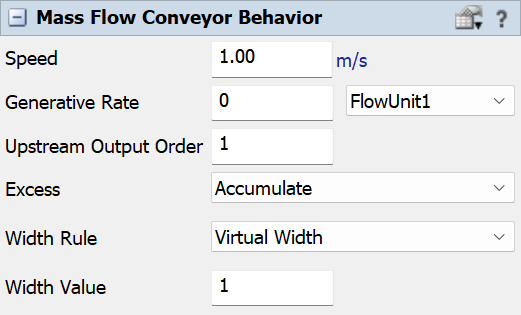
このパネルには、次のプロパティがあります。

速度

コンベヤの速度を定義します。

生成ﾚｰﾄ

コンベヤをソースとしてマスフロー単位を生成するとき使用します。モデル時間単位ごとの単位数としてレートを定義し、生成するフロー単位を定義します。たとえば、ビン詰めラインをシミュレートするとき、モデルが分単位で定義されているなら、生成レート100は、コンベヤで1分ごとに100本のボトルが生成されることを意味します。

上流出力順序

出力フローを分配するとき、上流のコンベヤによって、このコンベヤが選択される順序を定義します。この設定は、1つの上流コンベヤに複数の下流コンベヤが接続されていて、このコンベヤが下流コンベヤの1つである場合、言い換えれば、上流のコンベヤがフロー単位を送出するとき、複数の下流コンベヤのいずれかを選択する場合にのみ使用されます。詳細については、「フローを下流に分配する」を参照してください。

特殊な値0を使用すると、上流コンベヤがフローの分配を解決するときにこのコンベヤをまったく考慮しないようにすることもできます。これは、固定リソースで入力を閉じるのと同じ効果がありますが、それをマスフローコンベヤに対して行います。このフィールドに0を入力するか、次のようにプログラムで0を指定することができます。

conveyor.setProperty("UpstreamOutputOrder", 0);

過剰

下流に送出できない過剰分のフローをどのように処理するかを定義します。［集積］が選択されていれば、過剰分はコンベヤに集積されます。［損失として追跡］が選択されていれば、過剰分のフローはコンベヤの終端から落ちたのと同様に、損失として追跡されます。詳細については、「フローを下流に分配する」を参照してください。

幅の規則

コンベヤのシミュレーション幅を決定するための規則を定義します。［幅値］と組み合わせて使用します。

シミュレーション幅がコンベヤの動作にどのように影響するかについては、「マスフローコンベヤの背後で行われる計算」を参照してください。幅の規則を使用すると、同セクションの方程式で使用する$W$値をどのように決定するかをカスタマイズできます。ここでは、同セクションと同じ表記法を使用して、コンベヤのシミュレーション幅を$W$、ユーザーが定義する［幅値］を$V$と表します。

  • ｺﾝﾍﾞﾔ幅 - 標準の［幅］プロパティを使用します。

    • $W = \text{コンベヤ幅}$

  • 仮想幅 - シミュレーション幅は［幅値］です。

    • $W = V$

  • ﾚｰﾝ数 - シミュレーション幅を計算するとき、ユーザーが定義した単位レーン数がコンベヤ上を移動するものと仮定します。目的のレーン数を［幅値］に入力します。

    • $W = V \cdot \Large{\frac{U_y}{R}}$

    この方程式を見ればわかるように、値$\frac{U_y}{R}$は基本的に、コンベヤを流れる単位の単一レーンの幅となっています。$U_y$は1つの単位の幅であり、$R$は丸いボトルの密度係数です。そのため、$V$は、ユーザーがシミュレートしたいレーン数までコンベヤ幅を拡大縮小する機能を持ちます。

    重要なのは、この規則でも他の規則でも、小数値が完全に有効であるという点です。たとえば、ここで幅値として0.5と入力した場合、単一レーンフローの「2分の1」がシミュレートされます。これは、各単位（カートン、ボトルなど）の間に$U_x$分の「エアギャップ」がある単一レーン単位と基本的に同じです。次に説明する［単一ﾚｰﾝﾌﾛｰ単位距離］規則と似ていますが、同規則では単位間の距離が固定であるのに対して、［ﾚｰﾝ数］規則では単位間の距離が単位の長さに比例します。大きいボトルやカートンなどでは互いの距離が大きくなる、といった具合です。詳細については、「計算が重要な理由」を参照してください。

  • 単一ﾚｰﾝﾌﾛｰ単位距離 - シミュレーション幅は、単一レーンの単位をシミュレートするものとして計算されます。ただし、ある単位（ボトル、カートンなど）の中心から次の単位の中心までの距離をユーザーが定義できます。この距離を［幅値］に入力します。

    • $W = \Large{\frac{U_x}{V} \cdot \frac{U_y}{R}}$

    ここでも見ればわかるように、幅値$V$を単位長$U_x$と同じにした場合（つまり、単位間の距離が$U_x$の場合）、左の項は互いに相殺するため、$\frac{U_y}{R}$が残ります。つまりここでも、連続するボトルの単一レーンの幅となります。$V$を増やすと、単一レーン内のボトル間の距離が広がることになり、$W$は小さくなります。

  • 単一ﾚｰﾝｷﾞｬｯﾌﾟ - シミュレーション幅は、単一レーンの単位をシミュレートするものとして計算されますが、単位間にはユーザーが定義した「エアギャップ」があるものとします。「エアギャップ」とは、ある単位の後部から次の単位の前部までの距離です。この「エアギャップ」の距離を［幅値］に入力します。

    • $W = \Large{\frac{U_x}{U_x + V} \cdot \frac{U_y}{R}}$

幅値

［幅の規則］に関連する値を定義します。