Social Forces
Overview and Key Concepts
Social forces are calculated directional forces that are applied to agents who have a social force behavior active. These forces make up the individual components that, when added together, effect a cumulative force that accelerates the agent in a certain direction.
Equations
The user interface for forces will often display an equation that represents how the force is being calculated. You can get hints as to what each of the components of the equation means by clicking on the equation.
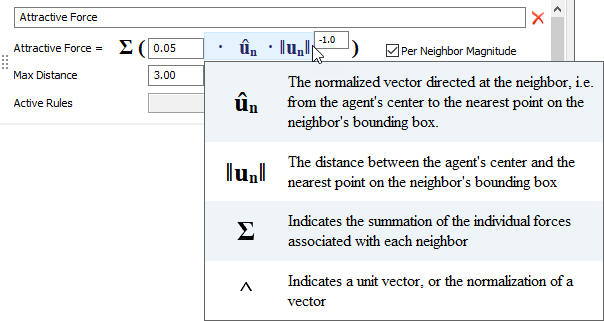
Equations are usually composed of a user-defined scale factor, which is multiplied by some directional unit vector. Then the result is subsequently multiplied by a factor that is dependent on the distance from the agent. You enter an exponent value to define how the distance from the neighbor agent affects the overall force calculation.
Let's take for example an attractive force, which attracts an agent towards its neighbors.
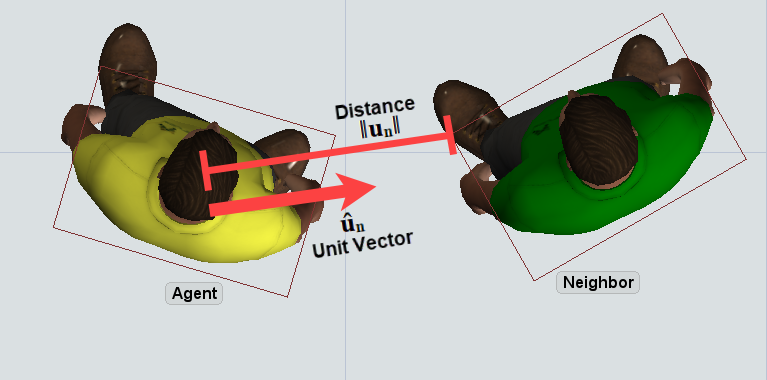
The symbol ûₙ represents the normalized (unit) vector directed at the neighbor, i.e. from the agent's center to the nearest point on the neighbor's bounding box. This unit vector is scaled by a scale factor that you can define. Then the result is again scaled by a factor that is dependent on the distance from the agent, represented by the symbol ‖uₙ‖.
As an example, let's say that ûₙ is the vector [0.97, 0.24], and that ‖uₙ‖ is 0.5, which is a rough estimate of the picture shown above. You have defined a scale factor of 0.1 and a distance exponent of -1. First the equation scales ûₙ by 0.1, resulting in the vector [0.097, 0.024], then it multiplies that vector by 0.5-1, or 2. Thus the resulting force, for that neighbor, is [0.194, 0.048].
fn = 0.1 · [0.97, 0.24] · 0.5-1 = [0.194, 0.048]
In this scenario, if no other forces are affecting the agent, then the agent will take on a directional acceleration of [0.194, 0.048].
Note the effects of the two user-defined values in the equation. The scale factor — in this case 0.1 — serves to generally scale the force. You use this scale factor to adjust the strength of the force in relation to other forces that make up the social force behavior. The exponent value — in this case -1 — scales the force dependent on the distance from the agent. A value of -1 means that, as the distance gets larger, the force gets smaller, and as the distance gets smaller, the force gets larger. For an exponent value of -2, the inverse relationship between distance and force is even stronger, and would be synonymous with a gravity-like force. You could also give the exponent a value of 0, which means that distance has no effect on the force's magnitude. Alternately, if you give the exponent a positive value, then there will be a positive correlation between distance and force magnitude. As distance gets bigger, the force gets bigger.
A neighbor-based force, such as an attractive force, will sum all of the forces calculated for each of an agent's near neighbors. This summation is represented in the display of the equation with the Σ symbol.
Neighbor-based Forces
The neighbor-based forces are the following:
Attractive Force
As described above, the attractive force is a force that attracts an agent to its near neighbors. It calculates the force for each neighbor that is within the maximum distance, and then sums the individual forces together.

In addition to the scale value and exponent, the attractive force has the following properties:
- Max Distance – This defines the maximum detection distance for the force. The force will be applied only for neighbors that are within this distance.
- Per Neighbor Magnitude – This checkbox affects how the forces are summed together. When checked, forces will be calculated individually, and then summed together. Thus, if an agent has more neighbors, the force will be greater. On the other hand, if the box is unchecked, each neighbor force is first multiplied by the distance factor. Then forces are summed together. Finally, the sum force is normalized and multiplied by the scale factor. In this configuration, you are essentially defining a static force magnitude, in the direction of the center of mass of the agent's neighbors. In other words, the force will be the same magnitude — namely the scale factor you enter — no matter how many near neighbors there are. This configuration is what is called a cohesive force.
- Active Rules - See Social Force System: Behavior Tab for more information about Active Rules.
Repulsive Force
A repulsive force is similar to an attractive force but applied in the opposite direction, namely away from neighbor agents. In addition to standard attractive force properties, it has the following:
- Hard Limit – This is an added field for repulsive forces. It determines a minimum distance that an agent must keep from its near neighbors.
Cohesive Force
The cohesive force attracts the agent to the 'center of mass' of its neighbor agents. The cohesive is an attractive force where the Per Neighbor Magnitude is unchecked.
Transverse Force
A transverse force is applied when neighbors of the agent are traveling toward the agent. This force will push the agent to move to the right. The first field is the scale factor, its value will determine the direction: a positive value will cause the agent to move to the right, a negative value will cause the agent to move to the left. The second value is the exponent value.
- Field of View – This field determines the range in degrees that the agent will look for neighbors when applying this force.
- Travel Direction Threshold - The agent will only apply the force to neighbors whose travel direction is at least this many degrees offset from the agent’s travel direction.
- Max Distance – This defines the maximum detection distance for the force. The force will be applied only for neighbors that are within this distance.
Alignment Force
An alignment force is a force that motivates the agent to align its velocity with the velocity of its neighbors. For this force, the vector Δvₙ is calculated as the difference between the neighbor's velocity and the agent's velocity. In other words it is the force which, if applied to the agent, will change the agent's velocity to be the same as the neighbor's velocity.
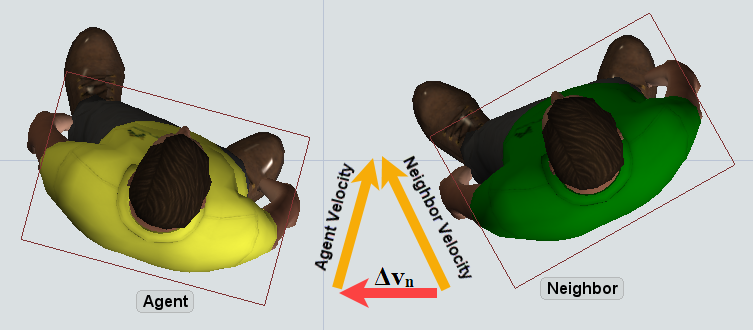
- Max Distance – This marks a finite distance from the agent where the force can be applied.
Self-based Forces
These are the following Self-based forces:
Friction Force
A friction force is applied in the opposite direction of an agent's travel.
- Static Friction – This is applied to the agent when stopped. Generally, this value is larger than the kinetic friction element. It acts as a threshold that means that the sum of other forces must exceed this value to get the agent to move.
- Kinetic Friction – This is applied to the agent that is moving, causing the agent to slow and stop when no other forces are pushing the agent. The exponent field will affect how the force is applied considering the velocity of the agent. A positive number means that the force is stronger as the velocity increases.
Momentum Force
A momentum force is the opposite of a friction force. It will push an agent to continue along its travel path. The first field is the scale factor, the second field is the exponent.
Goal-based Forces
A goal-based force will motivate the agent to move toward a goal. There are two possible forces here: a travel destination force, and an A* travel path force. If you define a goal-based force, you should choose one of these but not both.
Travel Destination
A travel destination force will take any travel tasks the agent is given and use the final destination location as a pulling force upon the agent, causing the agent to move towards its goal. As with other forces the first field is the scale factor, and there is an exponent field as well.
- Completion Threshold – This value defines how near the agent needs to be to the destination in order to designate the goal as finished, i.e. finish its travel task.
A* Travel Path
The A* travel path force will use elements from A* navigation to calculate forces. The agent system will communicate with the A* system to determine a path. Once the path is calculated, the agent will be motivated, through this force, to move along the path to its destination. As an agent moves along its path, it will have a current target node that acts as its current anchor to the path. The agent's path attraction is made of two primary forces associated with its current target node. The Node Attract Force attracts the agent directly to the node, whereas the Path Align Force motivates the agent to travel in the direction that the path is headed at the current target node.
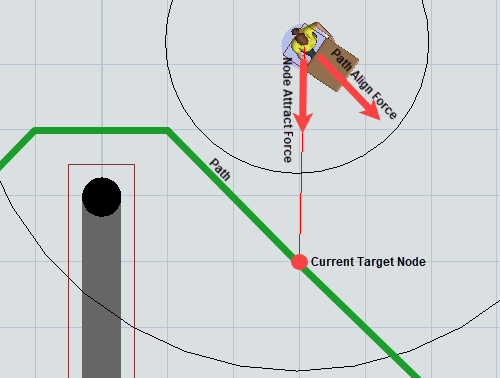
- Node Attract Force – This force is directed from the agent directly to its current target node. Again you can enter a scale factor and a distance-based exponent. Often a positive exponent is used, meaning that the farther the agent is from the path, the stronger the force will compel the agent to return to the path.
- Path Align Force – This force pushes the agent to move in the same direction as the path at its current node. The force is the vector location of the current target node on the path, minus the location of the last target node, normalized. Again you can enter a scale factor and a distance-based exponent. By default the exponent for the path align force is negative, meaning that the farther from the path the agent is, the more the node attract force will push the agent to return to the path first before aligning with it.
- Goal Force – This force pushes the agent to move towards the final goal. The first field is the scale factor for the vector, the second field is the exponent of the equation. The exponent by default is negative, meaning that the closer the agent approaches the goal the larger the force will compel the agent.
- Path Progression Angle – As the agent progresses on a travel path it updates its target node as it goes. This field defines a threshold for when to update the current target node. If the vector difference of the Node Attract Force and the Path Align Force are ever greater than this defined angle then the system will trigger a progression of the current target node.
- Position Difference Factor – This is field defines and second possible threshold for progressing the current target node. This is used in comparing the distance to the current target node, vs. the distance to the next target node. For example, if this value is 1.0, then the agent will progress its current target node when the distance to the next target node becomes less than the distance to its current target node. Usually this value will be in the range from 0 to 1. If it is 0.5, then the agent will progress its current target node if the distance to the next target node is less than half the distance to its current target node.
- Path Recalc Timeout – If an agent has been unable to progress along a travel path after the defined amount of time, the system will force the agent to recalculate a new path. This will keep agents from getting stuck in a deadlock.
- Completion Threshold – This determines the amount of distance the agent needs to be within to consider the goal task completed.
- Add Barriers as Static Agents – This box when checked makes barriers act as agents for determining forces. For example, repulsive forces will be used by the agent in regards to the barrier.
- Enforce A* Node Direction Limits – This will enforce hard limits on A* barriers, walls, dividers, etc. This will prevent agents from walking through walls, even if forces push them into them.
Custom Force
A Custom Force allows a force to be defined through custom code.
- Per Neighbor Force – This will cause the force to be applied to each neighbor.
- Max Distance – This will define a max distance for the force to be applied.
Random Force
This will apply a force compelling the Agent toward a random direction based on the defined magnitude.
- Magnitude - This defines the magnitude of the random force.