The Mass Flow Conveyor Behavior Panel

The Mass Flow Conveyor Behavior panel defines the behavior properties for a mass flow conveyor.

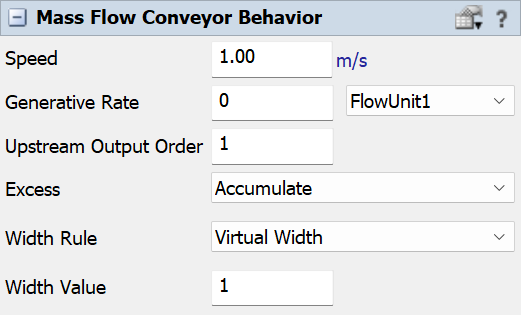
The following properties are on this panel:

Speed

Defines the speed of the conveyor.

Generative Rate

This is used if you want the conveyor to be a source that generates mass flow units. You define a rate, in units per model time unit, and the flow unit that is to be generated. For example, if you are simulating a bottling line, and your model is defined in minutes, then a generative rate of 100 means the conveyor will generate 100 bottles per minute.

Upstream Output Order

Defines the ordering by which this conveyor should be chosen by an upstream conveyor in distributing its output flow. This is only used when the conveyor is one of multiple downstream conveyors that is connected to a single upstream conveyor, in other words, when the conveyor upstream of this conveyor must choose between multiple downstream conveyors in sending flow units. See Distributing Flow Downstream for more information.

You can also use a special value of 0 to cause upstream conveyors not to consider this conveyor at all in resolving flow distributions. This has the same effect as closing input on fixed resources, but for a mass flow conveyor. You can either enter 0 in the field, or do it programmatically:

conveyor.setProperty("UpstreamOutputOrder", 0);

Excess

Defines how the conveyor should handle excess flow that cannot be sent downstream. If Accumulate is chosen, then the excess will accumulate on the conveyor. If Track as Loss is chosen, then any excess flow will be tracked as loss, as if the product were to fall off the end of the conveyor. See Distributing Flow Downstream for more information.

Width Rule

Defines a rule for determining the simulated width of the conveyor. This is used in combination with the Width Value.

For detailed information on how the simulated width affects conveyor behavior, see The Math Behind Mass Flow Conveyors. The width rule lets you customize how the $W$ value in those math equations is determined. Here we use the same notation, defining $W$ as the simulated width of the conveyor, and introducting $V$ as the user-defined width value.

  • Conveyor Width - Uses the standard Width property.

    • $W = \text{conveyor width}$

  • Virtual Width - The simulated width is the Width Value.

    • $W = V$

  • Number of Lanes - The simulated width is calculated so as to simulate a user-defined number of unit lanes traveling down the conveyor. Enter the desired number of lanes as the Width Value.

    • $W = V \cdot \Large{\frac{U_y}{R}}$

    For intuition on this equation, note that the value $\frac{U_y}{R}$ is essentially the width associated with a single lane of units flowing down the conveyor: $U_y$ is the width of a single unit, and $R$ is the round-bottle density factor. $V$ therefore serves to scale the conveyor width to be the number of lanes you want to simulate.

    It's important to remember that, for this and other rules, fractional values are perfectly valid. For example, if you were to enter 0.5 as the width value here, it would simulate 'one half' of a single lane of flow. This is essentially the same as a single lane of units with an 'air gap' of $U_x$ between each unit/carton/bottle/etc. This is similar to the Single Lane Flow Unit Distance rule described below, except that, in that rule, the inter-unit distance is fixed, while in this rule, the inter-unit distance scales with the unit's length. Bigger bottles/cartons/etc. would have larger distances between each other, and so forth. See Why Does the Math Matter? for more information.

  • Single Lane Flow Unit Distance - The simulated width is calculated so as to simulate a single lane of units, where you can define the distance from the center of one unit/bottle/carton/etc. to the center of the next unit. Enter this distance as the Width Value.

    • $W = \Large{\frac{U_x}{V} \cdot \frac{U_y}{R}}$

    Again for intuition here, note that, if you were to enter the width value $V$ as the same as the unit length $U_x$, i.e. an inter-unit distance of $U_x$, the left term would cancel out and you would be left with $\frac{U_y}{R}$, which again is the width associated with a single lane of back-to-back bottles. Increasing $V$ decreases $W$, meaning it extends the distance between bottles in the single lane.

  • Single Lane Gap - The simulated width is calculated so as to simulate a single lane of units with a user-defined 'air gap' between units, i.e. the distance from the back of one unit to the front of the next. Enter this 'air gap' distance as the Width Value.

    • $W = \Large{\frac{U_x}{U_x + V} \cdot \frac{U_y}{R}}$

Width Value

Defines a value associated with the Width Rule.