経験分布
概要と主要な概念
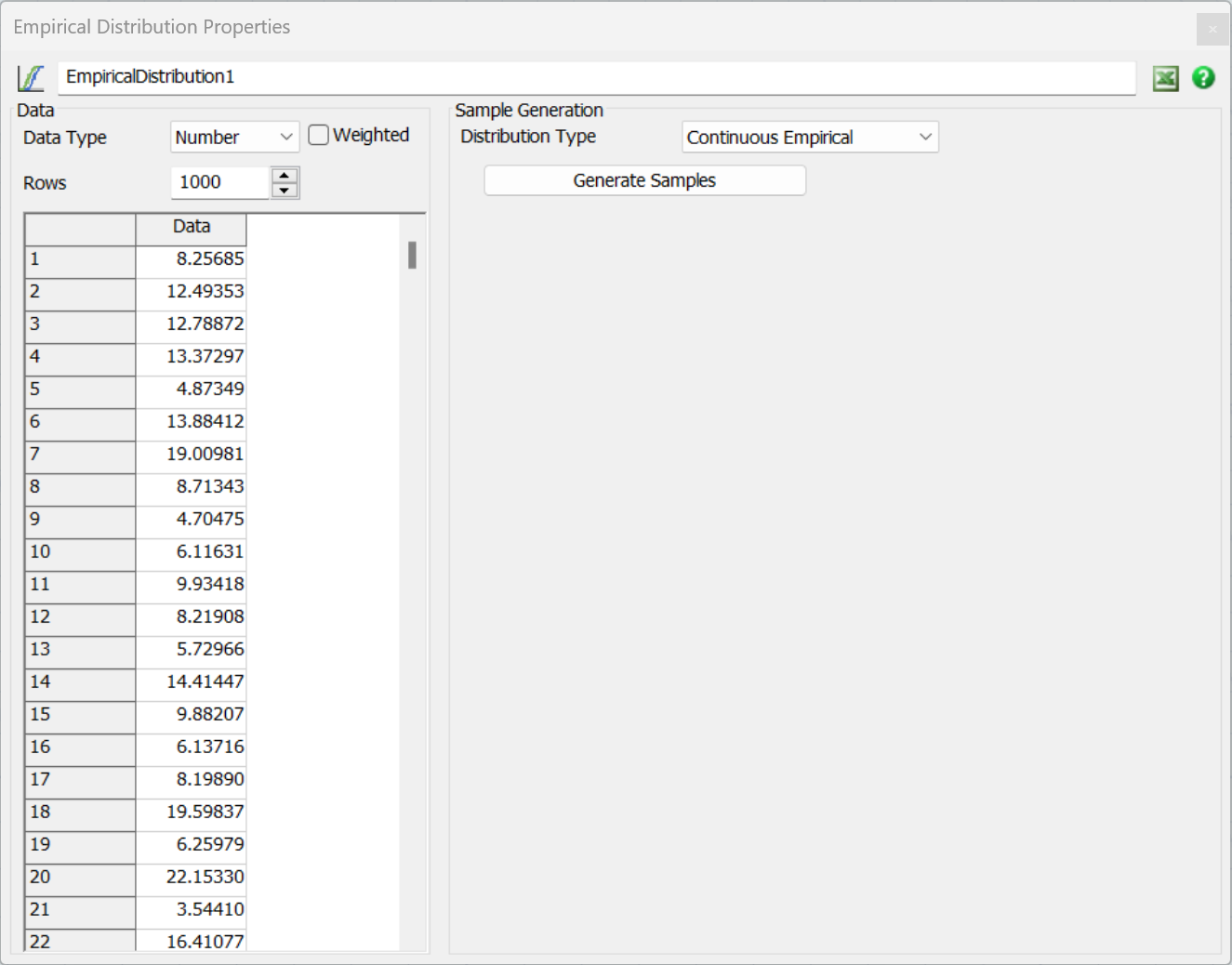
経験分布ツールは、経験データのテーブルを前提としてランダムな値を生成するために使用します。
経験分布ツールにはテーブルがあります。このテーブルがツールへの入力となります。テーブルには、履歴値または一般的な値が含まれている必要があります。これにより、経験分布ツールをランダム分布関数として使用することができます。経験分布ツールは入力データに基づいてランダムな値を生成します。ランダムな値の分布は、入力値の分布と一致します。
経験分布ツールは、ツールボックスからアクセスします。
データタイプ
経験分布ツールは、数字または文字列(テキスト)の値をサポートします。テキスト値を使用する場合、[分布タイプ]は自動的に[離散]に設定されます。
値の重み
[加重]チェックボックスをオンにすると、各値に重みを付けることができます。このチェックボックスをオンにしない場合、すべての値にデフォルトの重みが一様に適用されます。どちらの場合も、経験分布ツールは入力値を並べ替え、重複する値とそれらの重みをまとめます。
最終的に、特定の値の重みの総和を増やすことで、値(連続データの場合は隣接する複数の値)の尤度を高めることができます。重みの総和を増やすには、重みを直接指定するか、テーブルに値のインスタンスを追加します。
データ入力
入力テーブルへの値の設定は、手動で、あるいはExcelインターフェイスを使用して行うことができます。データは特定の順序にする必要がありません。Excelデータのインポートの詳細については、「Excelインターフェイス」を参照してください。
サンプル生成
[サンプル生成]ペインでは、経験データからランダムサンプルを生成する方法を定義できます。
経験分布ツールからランダム変量を生成する方法の詳細については、「経験分布API」を参照してください。フィールドがランダム分布を受け入れる場合、通常は経験分布ツールを使用できるピックリストオプションがあります。
分布タイプの選択
[分布タイプ]は次のいずれかの値に設定できます。
- 連続経験分布
- 離散経験分布
- 適合分布
連続経験分布
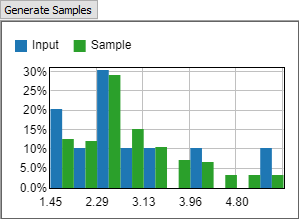
[連続経験分布]に設定すると、テーブル内の値は、処理時間などの連続分布に由来すると見なされます。ツールでサンプリングを行うと、最小値から最大値までの間の任意の値が返されます。特定の入力値が返される可能性は低いものの、戻り値の分布は入力値の分布と一致します。連続分布は、処理時間のデータに適しています。
[サンプリング生成]ボタンを使用すると、入力データとサンプリングされたランダムデータの両方を示すヒストグラムが表示されます。
離散経験分布
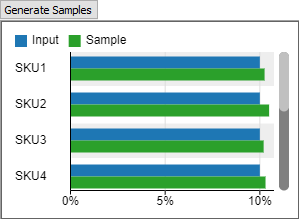
[離散経験分布]に設定すると、テーブル内の値は、可能性のあるすべての値であると見なされます。ツールでサンプリングを行うと、テーブル内の値のいずれかが返されます。特定の値の尤度は、入力データ内の頻度または重みによって決まります。離散分布は、注文のアイテム数といった離散値や、ランダムなSKUに適しています。
[サンプリング生成]ボタンを使用すると、入力データとサンプリングされたランダムデータの両方を示す棒グラフが表示されます。
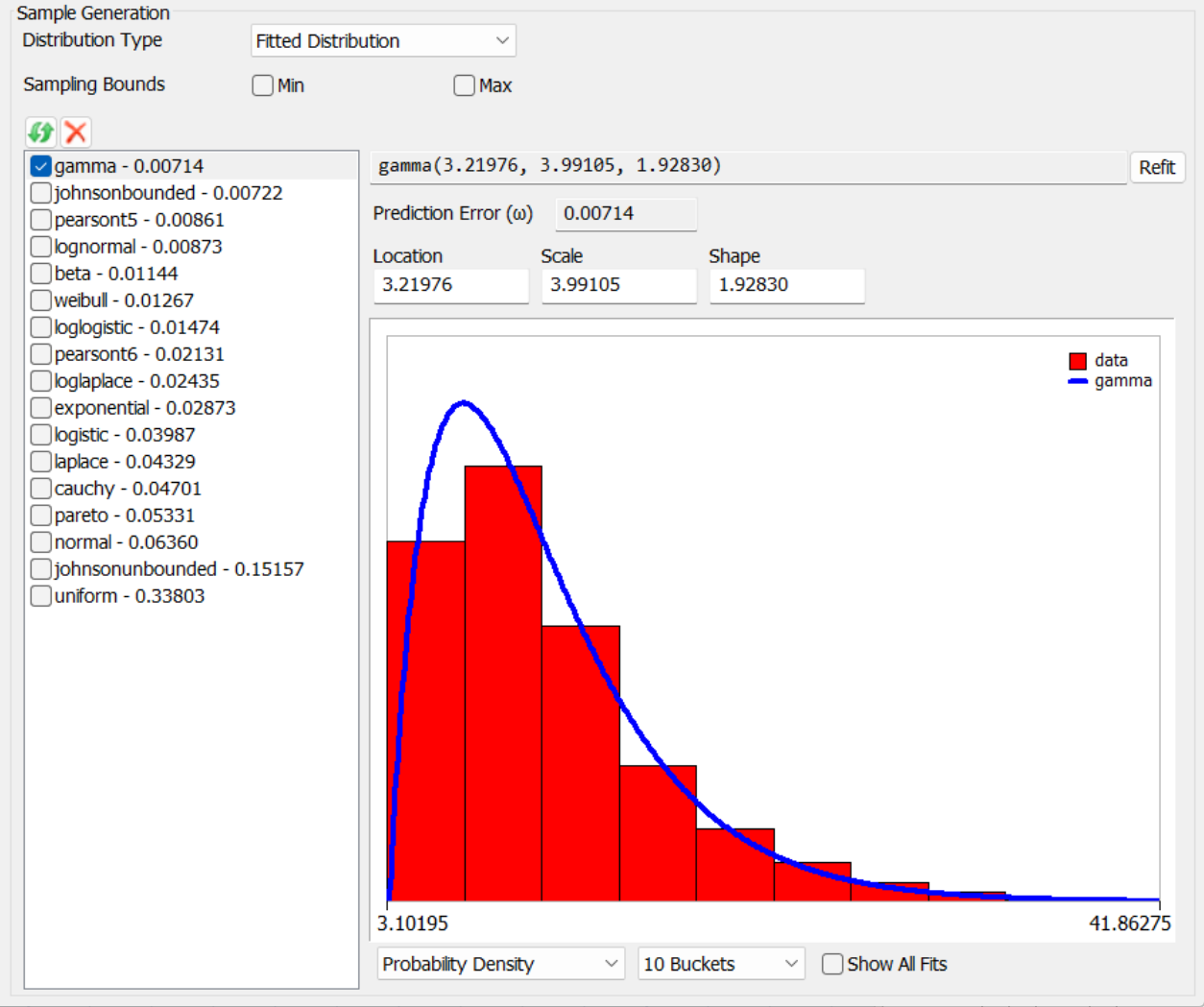
適合分布
[適合分布]に設定すると、追加のボタンとコントロールが表示され、データを既存の分布に適合させることができます。ツールでサンプリングを行うと、選択した適合分布からランダムサンプルが生成されます。
分布適合を生成するには、
各適合には、分布名、適合パラメータ、予測誤差(ω)が表示されます。予測誤差とは、この適合がデータにどの程度適合しているかを示す0~1のスコアです。小さい数値の方が優れています。
適合グラフの下にもコントロールがあり、確率密度関数または累積分布関数のいずれかと、バケット数などを表示できます。
最小と最大を定義する
分布の多くはテールが長い場合や必ずしも正の値を返さない場合があるため、ツールでは[最小]値と[最大]値を定義することもできます。これにより、生成したサンプルを残す値の範囲を定義できます。該当するチェックボックスをオンにし、サンプリングする範囲の最小値または最大値を入力してください。定義すると、サンプルが最小値/最大値の範囲に収まるまで、適合分布から繰り返しサンプリングが行われます。
曲線適合アルゴリズム
FlexSimは、パラメータ化された確率分布にデータを適合させるために、比較的単純な曲線適合アルゴリズムを使用しています。なお、FlexSimの曲線適合機能は、各種曲線適合のすべての統計分析を目的としたものではありません。その目的であれば、ExpertFit、Stat::Fit、scipy.optimize.curve_fitなどの市販の分布適合機能をご購入ください。弊社の経験上、データセットの多くは既知の分布にあまり適合しないため、経験分布ツールのデフォルトのオプションである[連続経験分布]オプションを使用して、データのリサンプリングを直接行うことをお勧めします。しかしながら、FlexSimの曲線適合機能も、一部のシナリオでは役立ちます。透明性を高めるため、ここでは、各種分布にデータを適合させるために使用されるアルゴリズムについて説明します。
FlexSimの曲線適合機能は、一般に知られた最尤推定量(maximum likelihood estimator:MLE)と最適化原則を融合させたもので、データを最もよく適合させる分布パラメータを見つけます。各分布族には、通常、パラメータに対して既知の最尤推定量がいくつか存在します。たとえば、正規分布のμパラメータのMLEはサンプルの平均であり、σパラメータのMLEはサンプルの標準偏差です。これらのMLEが既知の場合、FlexSimの曲線適合機能は単純にMLEを計算し、それをデータの「最良適合」として使用します。弊社は、既知のMLE計算を見つけるために、主にAverill Lawの『Simulation Modeling & Analysis, 5th Edition』を使用しました。
一部の分布族には、(少なくとも弊社から見て)既知のMLE計算のないパラメータがあります。たとえば、乱数生成関数の追加パラメータ(locationなど)は、こうした分布族の標準定義に含まれません。あるいは、これらのパラメータのMLE計算が単に文書化されていない場合もあります。ここではこれらを非MLEパラメータと呼びます。非MLEパラメータに関して、FlexSimの曲線適合機能は、最初の推定をそのパラメータの値で行い、次に反復的な勾配降下アルゴリズムを実行して、曲線に最も適合する値を見つけます。
勾配降下
勾配降下アルゴリズムの目標関数として、この適合機能は、Cramér-von Mises型の適合度テストを実行し、結果の
$\large{T} = \large{n \omega^2} = \Large{\frac{1}{12 n} + \sum\limits_{i=1}^{n}[\frac{2i - 1}{2n} - F(x_i)]^2 }$
最小化目標、そしてUIで「適合スコア」として表示される値はωです。
$\large{\omega} = \Large{\sqrt{\frac{T}{n}}}$
ω は常に0~1の値であり、値が小さいほど適合しています。
勾配降下アルゴリズムは、反復のたびに、まず現在のパラメータで目標を取得します。次に、各非MLEパラメータの部分勾配を計算するために、そのパラメータを少し調整し、目標を再評価します。さらに、複数の部分勾配を累積勾配にまとめ、勾配の方向に1ステップ進み、プロセスを繰り返します。
勾配降下のステップサイズは、アルゴリズムの進行に伴い調整されます。ステップサイズの値は1から始まり、アルゴリズムは前回の反復の勾配を記録します。反復のたびに、アルゴリズムは新しい勾配を確認し、その後で現在の勾配と前回の勾配のドット積を求めます。これは2つのベクトル間の角度の余弦です。この値が1に近い場合、つまり、現在の勾配が前回の勾配とほぼ同じ場合、ステップサイズは増えます。値が0に近い場合、つまり、勾配が大幅に変化した場合、ステップサイズは減ります。つまり、アルゴリズムは、同一方向を進む間は勢いがあるものの、最小値を中心に旋回を始めると動きが遅くなります。
反復の最大値が実行されるか、ステップサイズが現象して最小しきい値になるまで、アルゴリズムの処理は続きます。
免責事項
FlexSimの曲線適合機能は、データが適合分布に由来するかどうかに関する仮説検証は実行しません。単に、ωを最小化する勾配降下を実行し、パラメータと結果のωを示すだけです。また、この曲線適合機能では、データのヒストグラムと分布の確率密度関数を比較するグラフ、またはデータの経験分布関数と分布の累積分布関数を比較するグラフを表示することができます。この曲線適合機能は、適合中のデータが連続的であり、連続分布にのみ適合することを前提としています。さらに、必然的にこの曲線適合機能は勾配降下に関連する標準的な欠陥の影響を受け、解が極小値になる可能性があります。繰り返しになりますが、強力なフル機能の曲線適合機能が必要な場合は、サードパーティ製のソリューションをお求めください。